计算思维(Computational Thinking，简称CT)融合了解决问题、设计系统和理解人类行为等多种思维活动，已成为信息化和数字化进程加速的智能环境中重要的思维能力^[1].卡内基·梅隆大学(CMU)计算思维中心特别强调了计算思维对所有学科的重要性，指出没有计算思维就几乎不可能在任何学术领域进行研究^[2].计算思维教育在国际上受到高度关注.澳大利亚、英国、波兰、韩国等国先后将计算思维纳入课程大纲，以培养学生的信息技术能力和数字素养.截至2021年，已有55个国家正式加入全球最大的推动计算思维教育的主题活动——国际计算思维挑战赛(Bebras).我国教育部于2018年1月印发《普通高中信息技术课程标准(2017年版)》，“信息意识、计算思维、数字化学习与创新、信息社会责任”等逐渐进入人们的视野.2019年3月，教育部发布《2019年教育信息化和网络安全工作要点》，计划通过人工智能、计算机编程、大数据等技术推动学生计算思维的培养，表明我国对计算思维教育日趋重视.

国际上有大量研究证实，基于技术进行教学干预对学生的计算思维培养具有显著正向影响.譬如，宁可为等^[3]基于App Inventor编程应用开展初中信息技术课程教学，结果发现学生的计算思维能力显著提升；Chou^[4]将ScratchJr整合到编程课程中，发现幼儿的计算思维能力经过8周课程学习后有显著进步.但也有实验得出不同结论，岳彦龙等^[5]构建了人工智能案例驱动的Python编程教学模型，发现其对学生计算思维的干预作用不明显；Rodríguez-Martínez等^[6]设计了使用Scratch进行教学干预的实验组和在纸笔环境中教学的对照组，发现两组学生的计算思维成绩在统计学上没有显著差异.由此可见，技术支持型教学干预对学生计算思维培养的效果仍有待进一步检验.

综上，本研究拟通过元分析方法对2006年1月至2022年10月国内外的实证研究进行分析，重点探索技术支持型教学干预对学生计算思维的影响，以及学科、干预工具、评估工具、国家(地区)、不同学段、实验周期、样本量大小、性别对学生计算思维培养的调节作用，以期为计算思维培养的研究与实践提供理论依据和路径参考.

计算思维的概念出现于20世纪中后期，它源自物理、生物、工程等众多学科，而非仅来自计算机学科.1980年，Papert^[7]首次提出计算思维概念，他认为计算思维可以改变儿童跨领域思考的方式.这一观点与Berland等^[8]提出的“计算思维即将计算机作为工具进行思考的能力”相吻合.国际教育技术学会(International Society for Technology in Education，简称ISTE)认为计算思维是一种基于算法思维和自动化的问题解决过程^[9].《计算机教育与可持续竞争力》(简称“蓝皮书”)写道：计算思维是以信息获取和计算实现认知世界和问题解决的思想及方法论^[10].2006年，周以真发表《计算思维》，她将计算思维定义为一种能够清晰地将问题和解决方案用计算科学或人类行为有效执行出来的思维过程和思维能力，该定义被广泛认可^[11].

教学干预是一个约定俗成且意义较广的概念，泛指一切对学习者产生影响的介入手段^[12].尽管已被视为覆盖众多学科的思维模式，但计算思维的教育仍有待开发，特别是K-12学校.研究者们开展了大量培养计算思维的实证研究，这些研究大部分依赖一定的教学设计和技术且得到的结论有所差异，因此，本文重点关注不同类型的技术支持型教学干预对计算思维培养的影响.根据已有研究和纳入的文献，下文从计算思维教学干预的学科、干预工具和评估工具3个方面进行分析.

从理论上讲，计算思维可在多种学科培养过程中体现，其蕴含的抽象、分解和自动化素养能为学科方案设计和问题解决提供有效支撑，同时具体学科问题能为计算思维的培养提供情境支持.研究者们尝试在不同的教学环境中实施干预以促进学生计算思维的发展.从现有教学实践来看，编程教育是重要途径之一，如多召军等^[13]探究编程教育促进学生计算思维发展的内在机理，构建了分阶段和结构化的儿童编程学习活动的框架.在计算机和科学(数学、化学、物理和生物)课程中融入计算思维训练也是教学研究的主要内容.Peel等^[14]成功利用蛋白质合成进行计算思维教学.Bundy^[15]认为计算思维几乎影响所有学科，既包括科学领域，也包括人文领域.Kafai等^[16]提出通过参与其他学科实践来提高计算素养.Petrie^[17]发现计算思维能够为音乐和编程学习提供有效支持.这些研究都侧重于在特定学习环境的背景下考察计算思维培养的重要性，但少有研究对不同学科干预环境进行横向比较，元分析则提供了弥补该空缺的工具.

有效的教学工具可以在计算思维的培养过程中发挥增效提质的作用.由于在培养学生计算思维的过程中不可避免地涉及算法和逻辑，故传统的计算思维教学工具常常基于计算机语言进行开发设计.随着技术飞速发展，基于文本的单一形式的教学工具已不能满足K-12各学段计算思维培养的需求，图形或模块化的、游戏形式的教学工具被广泛应用.国外对促进计算思维的教学工具的研究较为丰富，大多学者认为选择计算思维教学工具应遵循“低地板，高天花”原则，即选择工具既要满足基础学习的需要，还要满足高级程序设计的需要.国内计算思维培养的工具则较为单一，常用的有Scratch和App Inventor，如熊秋娥等^[18]通过教学实践验证了Scratch可视化编程软件对学生计算思维能力的培养有显著促进作用.已有研究通常分析某一具体教学干预工具的效果，而缺乏对不同工具干预效果的比较.故本文将干预工具作为调节因素之一，主要目的在于检验不同教学干预工具对提升学生计算思维的差异性.

作为教学过程的重要环节，适切的评价和反馈也是研究者关注较多的干预措施之一.本研究参考已有研究^[19]将教学评估工具分为4类：第一类是基于编程任务的评价，一般将评价过程融入计算思维的培养过程，通常伴随学生编程任务的进行并及时给予反馈，如TDIA^[20]；第二类是基于量表的评价，即采用已开发的信效度较高的成熟量表进行测量，通过学生的量表得分反映计算思维能力，如CTt^[21]；第三类是基于试题的评价，往往建立在试卷和测试的基础上，以客观题的形式测量学生的计算思维能力，如Bebras国际测试；第四类是基于系统环境的评价，这类评价依托一定的计算思维培养的系统环境，通过系统设置固定的计算方式，自动收集学生计算思维的评价数据，在学习任务完成之后自动生成反馈和评价报告，如Dr.Scratch、Code Master、REACT.

除了干预工具、学科和评估工具会影响计算思维教学干预的效果，实验设计本身也会导致研究结果有所差异.首先，在教学实验中，参与者认知水平的差异会影响实验结果^[22].研究表明，培养低年级学生的计算思维比高年级学生有更显著的效果^[23].考虑到这一干扰因素，本研究以学段为调节因素探究其对计算思维培养的影响，并纵向比较技术支持型教学干预在什么学段对学生计算思维的影响最大.其次，作为实验设计的重要因素，样本量对学生计算思维的教学干预结果有显著影响^[24].因此，研究将样本量作为元分析的调节因素进行分析，测试样本量对学生计算思维的影响是否显著，为特定计算思维教学的学生人数设置提供新思路.在计算思维的培养中是否存在性别差异仍有争议.Atmatzidou等^[25]在教育机器人学习活动的背景下发现，与男孩相比，女孩似乎需要更多的训练时间才能达到相同的技能水平.然而，Milto等^[26]发现，在入门工程课程的机器人活动中，男性和女性实力相当.故本文将性别作为调节因素之一进行检验，探究性别对计算思维教学干预的效果是否有显著影响.最后，王胜兰等^[27]通过元分析发现，样本所在地区不同，教学干预对学生深度学习的影响有显著差异.据此可以推测，不同文化背景下的学生在认知方式和学习习惯上存在差异，这可能会导致不同国家(地区)的样本在计算思维教学干预效果上有差异.对以上文献进行梳理，将学段、样本量、国家(地区)、性别也纳入调节因素，检验它们是否会在技术支持型教学干预与学生计算思维培养的影响效应中产生调节作用.

为尽可能囊括各个数据库中已有的文献样本，本研究在中国知网、维普、万方3大中文数据库，以及Web of Science、ProQuest Central、ERIC、Elsevier SDOL、Google Scholar 5个外文数据库进行了全面搜索，类型涵盖了期刊论文、学位论文和学术会议论文，时间跨度为2006年1月-2022年10月.

首先，对本研究的因变量展开检索，中文检索设置主题词为“计算思维”，外文以“computer thinking”为主题词检索；再运用各检索引擎的高级检索功能选择主题检索模式进行检索，并加入相关教学技术和工具(编程、编码、乐高等)，限制文献为实验研究或者案例，在检索框中输入检索公式“(Programming or Code or LOGO or Scratch or Robotics*)AND(Computational Thinking)AND(Research or Study or Case)”，其他检索条件设为默认，运行检索并将所得文献导出汇总，共获得文献472篇.在此基础上，依据第一轮检索的文献所提供的参考文献进行第二轮检索，以滚雪球的方式获得104篇与主题相关的文献，随后将两轮文献检索结果进行汇总和整理，删除重复文献32篇，共产生544篇可供进一步筛选分析的候选文献.

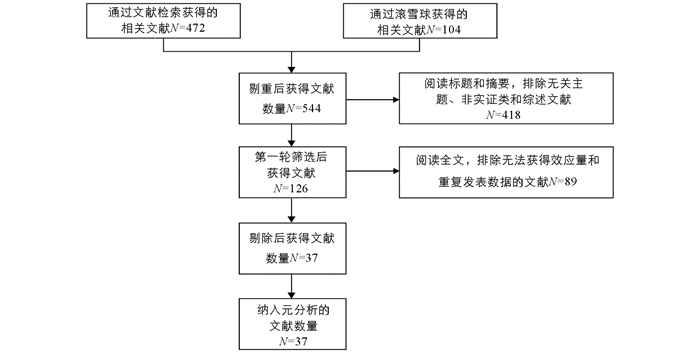
根据Meta分析的文献输入要求，纳入的文献均需采用随机实验或准实验方法.由于不是所有文献都符合纳入要求，本研究制定了严格的遴选标准，包括以下4点：(1)研究为准实验或随机实验研究，且必须是实证研究.有实验组和对照组，或者有前测和后测的比较，有一定周期的干预并用实证研究的方法收集数据，否则予以排除.(2)研究主题与计算思维培养相关，计算思维是研究的因变量或者因变量结果的一部分.(3)研究需报告效应量或有足量用于计算效应量的数据信息，否则予以排除.(4)数据重复发表的研究选择其中一篇论文，其余研究则予以排除.根据以上标准进行纳入和排除文献的流程如图 1所示，筛选后共有37篇文献被纳入分析.

本研究对文献基本信息(作者和发表时间)、样本所在国家(地区)、干预的周期、样本量大小、学段、性别、学科、教学干预的工具、评估工具以及结果变量类型进行编码，同时提取和计算文献中能够衡量干预效果的效应量(表 2).若同一篇文章中出现多个独立样本，则分开编码.

为确保纳入研究的文献质量，本文参照Valentine等^[28]对文献质量的评估方法，从干预措施、样本特征、实验设计、测量工具和测量过程5个方面对文献质量赋分，“不清晰”为0分，“较清晰”为1分，“清晰”为2分，分数越高代表文献质量越高.经作者评分，本研究各文献得分范围在6~10分，表明纳入文献的质量基本满足元分析要求.

常用的元分析数据处理软件有Revman(Review Manager)、STATA、R和CMA(Comprehensive Meta Analysis)等，本文选用CMA 3.3软件进行Meta分析.当计算样本量小于20的研究的标准均值差时，应选用g值作为效应量指标以减小偏差^[29].本文有11项研究的样本量小于20，故选用g值作为统一效应量指标.参考Ishinuki等^[30]的研究，当同一篇文章中出现多个测量维度时，研究使用StatsToDo网站合并多个维度的均值和方差作为该文章的总均值和方差.

需要注意的是，Borenstein等^[31]发现当一篇文章有多个独立研究而产生多个效应量时，可能导致文献占比过重而使结果产生偏差.故研究运用CMA3.3软件将这部分实验的效应量合并作为该研究的最终效应量，效应量的置信区间(CI)为95%.

鉴于CMA3.3可以直接得出I²值，因此本研究选择I²检验来判断异质性.根据Higgins等人的标准，I²＜25%表示研究存在低异质性，25%≤I²≤75%表示研究存在中异质性，I²＞75%表示研究存在高异质性^[32].本研究样本的异质性检验结果显示I²为90.318%＞75%(见表 3)，说明研究样本间存在明显的高度异质性.Borenstein等^[31]指出，存在异质性时，应选取随机效应模型，因此，本研究采用随机模型计算合并效应值，同时进行调节变量分析，厘清异质性来源.

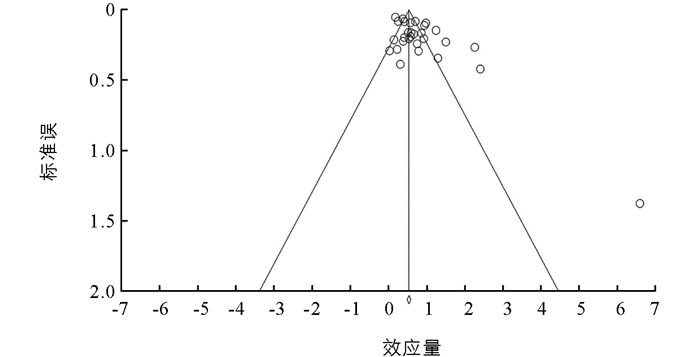
发表偏倚指科学研究的传播受到发表、时滞、多重发表、地域、结果报告等多种因素影响，造成系统评价的偏差，即现有研究中大量存在的阳性结果，而对阴性结果加以忽视或排斥发表，造成Meta分析结果的偏倚.最常用的检测方法是漏斗法，本研究的大部分样本聚集在漏斗顶端，均匀分布在漏斗中心两侧，初步说明存在发表偏倚的可能性(图 2).为进一步验证，选择Egger法对发表偏倚的统计量进行检验，发现t=3.66(p＜0.05)，说明存在发表偏倚.采用剪补法进行修正，在随机模型条件下评估发表偏倚对研究结果稳健性的影响，没有纳入虚拟文献，前后结果未发生变化，说明发表偏倚对合并效应量不存在显著影响.

Classic失安全系数(Fail-safe N)主要评估有多少未发表的研究才能使得已经发表研究的总体效应值不显著.衡量标准为5*n+10，其中n代表本研究中纳入元分析的文献数量，CMA3.3得出本研究中失安全系数为6 761，远大于195(n=37).这表示还需要6 761个研究才能推翻本研究的结论，说明未发表研究的效应值对已经发表的总体效应值影响较小.

合并37篇文献的效应量作为结果变量，在选定随机效应模型下得出的合并效应量均大于0，且p值小于0.001，说明技术支持型教学干预对学生计算思维的培养具有显著正向影响.当0.2≤g＜0.5时，被认为是小效应，当0.5≤g＜0.8时具有中上等影响，大于0.8为大效应^[33].本研究的合并效应量g=0.780(95%CI、0.631~0.929)(表 3)，表明技术支持型教学干预对学生的计算思维培养具有中等以上的显著效应.

Brennan等^[34]将计算思维划分为计算思维概念、计算思维实践和计算思维态度3个内容维度，该框架在计算思维研究中被广泛引用^[35].在37篇文献的45项独立研究中，有30项研究关注计算思维的整体效果，8项研究关注计算思维概念，6项研究关注计算思维概念和实践.如表 4所示，尽管组间效应的差异不显著(p＞0.05)，但从效应量大小比较来看，仅关注计算思维概念的教学干预效果最差，对计算思维概念和实践进行整合干预的效果最好.

本研究中，依托编程课(n=11)和STEAM课程(n=9)进行教学干预最为常见(表 5).编程课、计算机科学、西班牙语课和信息技术课的g值均为超过0.8的大效应量，但是西班牙语课的数据是由同一作者(zha2018)给予相同指导下的研究提供的数据，可能存在偏差.

对文献报告的技术型教学干预工具的类型进行调节效应检验，发现不同类型的技术型教学干预工具对学生计算思维的培养没有显著差异(p＞0.05)(表 6).从双尾检验的结果来看，图形或模块化的编程语言、游戏化的编程环境、开源电子原型平台均对学生的计算思维培养产生显著正向影响.其中游戏化编程环境的合并效应量最大(g=0.993)，图形或模块化编程语言次之(g=0.818).

将37项研究的评估工具分为基于编程任务的评价(n=12)、基于量表的评价(n=11)、基于试题的评价(n=11)和基于系统环境的评价(n=9)4类(表 7).整体来看，4类计算思维评价工具都对计算思维教学干预的效果具有显著的积极效应(p＜0.001).从组间效应来看，4类评估工具存在显著性差异(p＜0.001).基于系统环境的评价具有最大的合并效应量(g=1.520＞0.8)，其次是基于量表的评价工具(g=0.846).

不同国家(地区)在计算思维教学干预效果上有显著差异(Q=88.122，p＜0.001)(表 8).结合各组的合并效应值和双尾检验的结果，中国台湾、中国香港、印度尼西亚、美国、土耳其教学干预的效果较好，韩国、希腊、新加坡教学干预的效果相对较差，其余国家的教学干预效果不显著(p＞0.05).

为进一步探究不同周期的技术型教学干预对学生计算思维培养的影响，将文献报告的实验周期划分为0~5周、6~11周和12周及以上3类.由表 9可知，3类干预周期都对计算思维的培养产生显著影响(p＜0.01).对比效应量值发现，实验效应量由大到小依次为6~11周(g=0.866)＞0~5周(g=0.700)＞12周及以上(g=0.680).从组间效应来看，3类实验周期的教学干预效果没有显著性差异(p＞0.05).

本研究将样本量分为0~30、31~50、51~100、101及以上4组，组间效应差异显著(p＜0.01)(表 10)，表明样本量对技术型教学干预的效果有影响.样本量为0~30的组(n=18)和样本量为31~50的组(n=8)均达到了大效应，样本量在101及以上的组仅表现为小效应.

由双尾检验的结果可知，技术支持型教学干预对不同学段学生计算思维的培养均有显著影响(p＜0.05)，各学段的调节作用效果表现不同(p＜0.05)(表 11).由于大学阶段的样本量较少(n=1)，所以主要比较学前至高中4个阶段.从效应值(g)大小来看，技术支持型教学干预对初中阶段学生计算思维培养的作用效应值最大(g=1.615，p＜0.001)，其次是学前阶段(g=0.891，p＜0.001)，小学阶段和高中阶段产生了相同大小的效应值(g=0.625，p＜0.001).

为探究计算思维的培养是否受到性别影响，本研究对样本的男性比例进行了统计，由于男性比例数据是连续性变量，故采用元回归分析进行检验.通过元回归分析，选取随机效应模型，获得回归模型的F=0.04(p＞0.05)不显著，可知计算思维的培养在性别上没有显著的统计学差异.

本研究采用元分析方法，分析了国际上37篇技术支持型教学干预对学生计算思维培养的实证研究，从主效应检验的结果看，技术支持型教学干预对学生计算思维的促进作用达到了显著水平(p＜0.001)，且95%CI下限大于0，合成后的效应量g=0.780，为中等效应，表明技术支持型教学干预对计算思维具有中等程度的显著正向影响.对比马志强等^[36]关于计算思维教学的元分析研究(SDM=0.35)，本研究得到的合并效应量明显更大.相较而言，本研究更为综合地考虑了技术支持型教学干预对学生计算思维培养的影响，内容更为全面，研究对象更为广泛，且对多个可能影响研究结果的调节变量进行了分析，经过严格的结果稳定性检验，研究结论可信度高.

如前所述，不管是关注计算思维整体，亦或计算思维的不同维度，合并效应量值都较为可观，均获得了中等及以上的效应量大小，且不存在显著的组间差异(p＞0.05).相对计算思维的实践和态度，研究者们更多地探讨了学生计算思维整体和概念认知的培养.但本研究结果表明，仅关注计算思维概念的干预效果相对其他3组(计算思维整体、计算思维概念和实践、计算思维实践)偏低.作为一种在大数据时代、人工智能环境中生存所需的习得性技能，计算思维的培养是全面、系统、长期的过程.研究者需要多维立体地关注学习者的计算思维培养，结合计算思维的科学本质和内在范畴设计教学干预方案.

本研究通过调节效应检验进一步分析了各研究结果间存在差异的原因.整体来说，纳入调节变量的因素主要有两类：一类是关于教学干预的变量，包含本研究选取的学科、干预工具和评估工具3个角度，对这类调节变量的分析便于了解哪些教学干预措施和工具更为有效；另一类是实验设计本身差异造成的不同，如考虑到计算思维教育在各国和各地区的实施方式不同，或由于受到不同硬件和软件环境的影响，可推测国家和地区因素会对实验结果造成一定影响.同时，除了外在的地域差异外，实验设计本身的样本量大小、样本中男女生的结构占比、被试样本的学段以及干预周期也是影响实验结果的重要因素.

不同学科中计算思维的教学干预效果呈现出显著的组间差异.英语和信息学课程中计算思维教学的效果不显著，在西班牙语和舞蹈课上教授计算思维却产生了显著效应，这说明本研究无法求证在非计算机相关或非编程类学科中教授计算思维是否有效.有研究对该问题进行了探讨，如Ye等^[37]对55项研究的元分析发现，计算思维与非STEAM学科领域(包括语言学习、社会科学和音乐等)整合的研究具有显著效应.目前这方面的实证研究数量仍较少，但很多研究已表明在计算机科学以外的领域开展计算思维教育极具潜力.还有学者指出在教学过程中将问题情境设置在真实场景中并给予学生展示机会，能显著提升学生的计算思维在各学科的迁移和运用能力^[38].

研究发现，图形或模块化编程语言、游戏化编程环境的干预效果均为大效应，即这两类工具对学生的计算思维培养能够产生较大效益，这与傅骞等^[39]的研究相符.图形或模块化编程语言可降低学生的认知负荷、提升其学习兴趣.相对简单的高级编程语言对学生计算思维的培养效果不显著(p＞0.05).究其原因，相比图形或模块化的编程语言和基于游戏的编程语言，这类编程语言(如Python、Java、Ruby等)的学习形式主要围绕语法展开，内容较为枯燥，对学习者而言难度较高.然而，也有研究指出^[40]，选择的计算思维教学工具并不是越简单越好，工具与教学对象之间有高度适配性才能产生好的教学效果.此外，选择计算思维教学工具时除了考虑学习者的基础，还应注意教学目标是否契合.因为大部分计算系统或工具最初的设计目标是满足用户的广泛需求，而非专门为培养计算思维所开发.因此，在教育教学实践中，所选用的工具需要兼顾不断训练学生计算思维各方面能力的功能以及满足学生解决问题和进阶学习的需要.

对学生的计算思维进行评价是课堂教学的关键一环.经调节效应检验发现，4类评价工具的效果具有显著差异(p＜0.05)，其中基于系统环境的评价工具达到相对较大的效应量(g=1.520).目前对计算思维的评估大多倾向于在各种系统环境中进行，以检查学生在特定平台产生的学习结果.如Koh等^[41]开发了一个实时计算思维评估系统，强调对学生创建的游戏或模拟进行语义分析.基于系统环境的评价主要是利用学习系统来评估学习者的学习过程并自动生成过程性评价的数据，进而反馈真实全面的评价结果.这一特征与计算思维在问题解决情境中的思维过程相吻合，能在学生的学习过程中提供较为及时准确的反馈.但这种评价方式相对其他几类工具而言，对技术开发的要求较高.单一评价工具不能适用于所有的教育情境，综合使用多种评价工具是一种必然的趋势.目前，计算思维评价工具大多是由欧美学者开发的，国内在自主开发本土化的计算思维评价工具方面仍有很大的发展空间.教育者要合理看待国外开发设计的评价工具，直接编译和引入的评价工具不能很好地适应我国的课程和教学环境，需从实践研究出发，以科学探究的结果作为研发工具的参照，自主研发更有针对性的评价工具，以促进计算思维教育的发展.

本研究中不同国家之间计算思维的教学干预情况具有显著的组间差异(Q=88.122，p＜0.001)，这说明实验所在国家与计算思维教育干预的效果显著相关.不同干预周期对计算思维教学干预没有显著影响，但6~11周的干预周期能够获得相对更大的干预成效(g=0.866).

就样本量而言，不同大小的样本量在计算思维教学干预的效果上呈现显著差异，小班教学干预的效果更好.与大班教学相比，小班教学中可以配置的教学资源占整体资源的比例会增加，教师有更多的教学时间，更易进行班级管理和控制课堂节奏.但小班化教学对教师的素质要求往往更高，教育硬件和软件的投入也会增加.因此，未来计算思维的教学干预研究应探索适合不同班级规模的教学模式，教育者应根据自己的需求和情况控制班级规模.

本研究中，初中生的计算思维教学干预取得了较好效果.瑞士认知心理学家皮亚杰(Jean Piaget)认为，初中阶段(12~15岁)的孩子开始出现接近成人水平的抽象逻辑思维能力，故与计算思维相关的概念认知和技能增长较快，这可能是原因之一^[42].在我国，计算思维的培养正由高等教育向中小学教育迁移，虽然已有部分研究成果围绕小学生计算思维的发展进行了初步探讨，但我国对基础教育开展计算思维培养的重视程度仍然不足.当前的首要任务是建立以中等和高等教育阶段为主且相互衔接的计算思维培养一体化路径，从实践层面加强学习环境建设，构建支持计算思维发展的横向和纵向生态系统.另一方面，需要积极推进计算思维培养学段下移.计算思维在K-12落地已是必然的趋势，将深刻影响一国未来的科技竞争力和创新力.在后续研究中，教育者应关注计算思维对中小学生核心素养发展的促进作用，设计适合我国中小学生的科学方案.这需要政府、学校和社会多方面的协同联动，加快推进计算思维教育的普及.

本研究对性别进行了元回归分析，发现性别对学生的计算思维培养未产生显著影响(p＞0.05).然而，现实中仍存在诸多性别刻板印象.早在20世纪初就有研究发现，由于在计算机科学、数学、环境科学与电子工程等领域中，男性人数远超女性，故女性对这些领域的信心和兴趣持续降低.有研究发现，女性可以更专注地进行编程和计算机学习，如Nourbakhsh等^[43]对高中机器人课程中的性别差异进行研究，发现女孩比男孩更专注；鉴于此，计算思维的教学应注意避免由刻板印象造成教学资源分配不均的可能性，并且积极对学生进行正向鼓励以提升学生学习的自信心.

本研究运用元分析方法，系统整理了国内外技术支持型教学干预对学生计算思维培养影响的实证研究，可为后续开展计算思维培养的理论研究和教学实践提供理论依据和路径参考.但受纳入的文献信息所限，本研究未能证实在非计算机相关或非编程类学科中教授计算思维是否有效.值得注意的是，不同的教学方式(如问题解决教学、项目式教学、合作教学等)、教学评价(形成性评价、总结性评价等)、不同的实验类型(如前实验、准实验、随机实验)也是影响学生计算思维的重要因素.此外，国内外有关计算思维态度倾向的研究较少，但有学者意识到态度倾向和自信心在学生计算思维培养过程中的重要性^[44].期待有更多的教学干预实验提供相关信息，例如关注不插电式、基于纸笔的计算思维教学干预模式，以针对不同阶段、不同基础的学生进行多样化的设计与指导.