-
开放科学(资源服务)标识码(OSID):

-
为实现“力争2030年实现碳达峰,2060年实现碳中和”的“双碳”目标,我国政府积极推动新能源汽车产业的发展. 锂离子电池由于其能量密度高、循环寿命长、功率密度高和自放电率低等优点[1-2]而被广泛用作电动汽车储能元件. 锂离子电池的容量和内阻分别是表征电池系统能量和功率特性的重要参数. 在电动汽车整车层面,电池容量决定了一次充满电后电动汽车的最大行驶里程,内阻则决定了电动汽车输出的最大功率;在电池管理系统(battery management system,BMS)层面,容量和内阻则是电池关键状态估计算法和寿命预测算法的必要输入. 因此,准确估计电池容量和内阻可以帮助用户实时了解电池状态,帮助BMS更准确地评估电池系统性能.
电池容量和内阻的估计方法可以分为两大类[3]:基于模型的方法和数据驱动的方法. 基于模型的估计方法的重点在于建立能够描述电池衰减过程的物理模型,再结合电池的实验数据,利用滤波算法[4-6]更新模型参数,从而实现电池的状态估计. 这类方法的泛化能力有限,且对参数的敏感性较高. 数据驱动的方法通常不需要对电池机理深入理解,而是基于大量电池实验数据,应用机器学习算法拟合电池健康特征(health indicator,HI)与电池状态变量之间的复杂映射关系,如相关向量机[7]、梯度提升树[8]以及各种神经网络算法[9-10].
随着计算机技术的发展,数据驱动模型得到广泛关注. 但现有的数据驱动模型通常仅聚焦电池单一状态的估计或预测,且需要大量的实验数据训练模型,导致数据收集的时间和经济成本较高. 针对上述问题,本文提出了一种基于弹性网络算法的电池容量和内阻估计模型,提取充电片段的容量增量作为模型特征,经过基于重采样的特征重构,可以使用相同的特征实现高精度的容量和内阻协同估计,并且对训练样本的需求量不大. 本文还提出了基于容量和内阻双参量的“三段式”电池评价方法,从而更全面地评价电池系统性能.
全文HTML
-
本文应用了德国卡尔斯鲁厄理工学院(KIT)公开的电池老化试验数据集[11](下文简称KIT数据集)进行研究. KIT数据集包含了3种不同正极材料的三元锂电池在不同温度和不同充放电倍率下循环测试的实验数据,具体的实验设置可以参考文献[11]. 本文使用了KIT数据集中的部分电池作为研究样本,如表 1所示,并将表中所示3类电池样本分别简记为NCM(25 ℃)、NCM(45 ℃)和NCA(25 ℃).
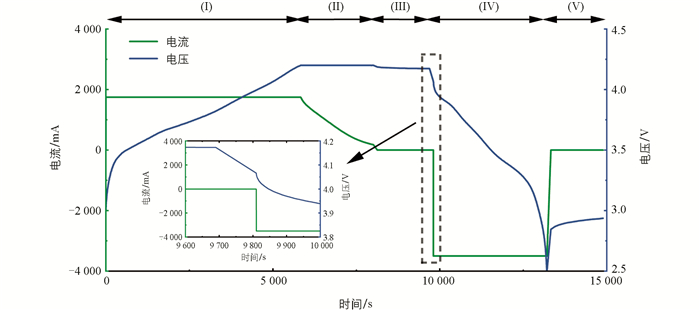
数据集中电池一个完整的充放电循环包括5个部分,如图 1所示,即(I)恒流(CC)充电、(II)恒压(CV)充电、(III)充电后的弛豫阶段、(IV)CC放电和(V)放电后的弛豫阶段,充电弛豫阶段后的放电电流电压瞬态响应如图 1中子图所示. 本文的电池容量以CC-CV充电的电流时间积分计算,电池的直流内阻由式(1)近似计算:
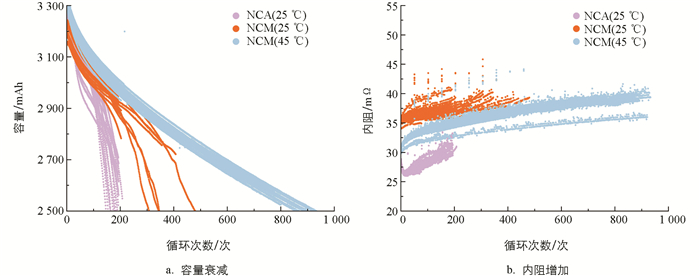
式中:Vrelaxation,end为充电后弛豫时间的最后一个采样点,VCCdischarge,start为CC放电的第一个采样点,ICCdischarge为CC放电电流. 图 2a和图 2b分别为3种电池随着循环次数增加而产生的容量衰减和内阻增加的示意图.
-
在电动汽车这一应用场景中,动力电池的放电过程受随机因素影响很大,难以从中提取出通用且稳定的数据特征来表征电池的健康状态[12]. 相比之下,电池的充电过程都遵循特定的充电协议,其工况相对稳定,便于从中提取特征. 本文使用从恒流充电过程中提取的容量增量(incremental capacity,IC)特征进行建模. IC特征是一种与电池老化状态相关性极强的特征[13],在电池健康状态估计研究中应用广泛. IC特征的计算方法为:
式中:t,I,V和Q分别为电池充电过程中的时间、电流、电压和容量.
为了保证模型具有固定长度的输入,进行了如下所述的重采样过程[14]以重构特征向量. 用Dm={(tim,Iim,Vim)|i=1,2,…,n}表示CC充电过程中的时间、电流和电压的实测值集合,其中:上标m代表测量值,n表示采样点总数,Iim和Vim分别表示对应采样时刻tim的电流和电压. 在一个指定的电压区间[Vl,Vh]以相等的采样间隔ΔV取k个电压采样点,则该区间的电压数据可表示为:
式中:Vi表示重采样后的电压,k表示采样点数量. k的计算方法为:
此时,可以通过对Dm中与Vi数值最接近的电压实测值Vim和Vi+1m及对应的采样时间tim和ti+1m进行线性插值:
移项得到对应于重采样电压Vi的重采样时间ti:
同理可得重采样电流Ii的计算公式为:
根据式(1)到式(7),对于CC充电过程中一个给定的电压区间[Vl,Vh]和采样间隔ΔV,总能得到重采样的充电片段数据D={(ti,Ii,Vi)|i=1,2,…,k},从而可将式(2)所示的IC计算公式改写为:
得到对应于重采样电压Vi的容量增量特征.
由于电动汽车用户充电行为的不确定性,越接近满电时的充电数据有越大概率被获取,因此本文仅使用电池CC充电至电压为4.0~4.2 V的片段数据计算IC特征,即重采样的电压值区间为[4.0,4.2],使用的重采样间隔为5 mV. 对于电池的每一个测试循环,都有40个IC值作为模型输入特征.
-
弹性网络(elastic net,EN)算法在本文被用作电池容量和内阻估计建模. EN模型是一个线性回归模型,是普通最小二乘法(ordinary least squares,OLS)的推广,其基本的数学表达式为:
式中:
$\hat{y}_{i}$ 是样本$i$ 的容量或内阻估计值,$\boldsymbol{X}_{i}$ 是样本$i$ 的$k$ 维特征向量,$\hat{b}$ 是线性方程的截距,$\hat{\boldsymbol{w}}^{\mathrm{T}}$ 表示$\boldsymbol{X}_{i}$ 的权重系数,通过最小化如下的损失函数得到:式中:arg min(·)函数的作用是找到使函数值最小的w值;
$\boldsymbol{y}$ 是表示电池容量或内阻真实值的n维向量(n是样本总数);X是n×k阶的系数矩阵,$\|\boldsymbol{y}-\boldsymbol{X} \boldsymbol{w}\|_{2}^{2}$ 是最小二乘法的计算公式;正则化强度系数α,是一个非负标量,用于控制正则化的强弱程度;P(w)是EN模型区别于OLS的正则化项. P(w)定义如下:式中:‖w‖1和‖w‖22分别表示w的L1和L2范数,ρ是正则化混合系数,用于控制L1和L2正则项的权重,取值范围在0到1之间.
-
为了获取合适的EN模型超参数,即正则化强度系数α和正则化混合系数ρ,结合K折交叉验证(K-fold Cross Validation)技术和网格搜索方法进行模型超参数的选择.
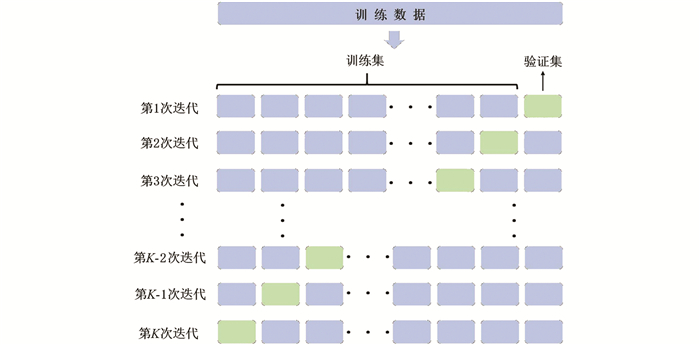
K折交叉验证的原理如图 3所示. 将训练数据拆分成K个大小相等的子集进行K次迭代,每个子集轮流做验证集,其余子集合并做训练集,迭代得到K个验证集的评价指标的均值作为交叉验证的最终结果. K折交叉验证可以在数据量有限时提高数据的利用率,使得模型的评估更稳健. 网格搜索是一种超参数选择方法. 其原理是,遍历模型超参数的所有可能取值组合,选择其中使得模型性能最佳的一组. 这一过程通常需要结合交叉验证使用,以避免选择结果受数据划分的随机性影响而出现较大偏差. 由于网格搜索所需的计算量较大、耗时较长,该方法通常在模型的超参数空间不大的情况下使用. 而对于仅有两个超参数的EN模型而言,网格搜索的计算耗时是可接受的. 结合K折交叉验证的网格搜索确定EN模型的超参数:对于容量估计,正则化强度系数α取42,正则化混合系数ρ取0.8;对于内阻估计,正则化强度系数α取1,正则化混合系数ρ取0.4.
3.1. 弹性网络算法原理
3.2. 模型超参数选择
-
本文采用了均方根误差(root mean square error,RMSE)和平均百分比绝对值误差(mean absolute percentage error,MAPE)来评价模型对容量和内阻的估计精度,二者的定义分别为:
式中:i表示测试样本编号,n表示测试样本总数,yi和
$\hat{y}_{i}$ 分别表示对应于样本i的真实值和模型估计值. -
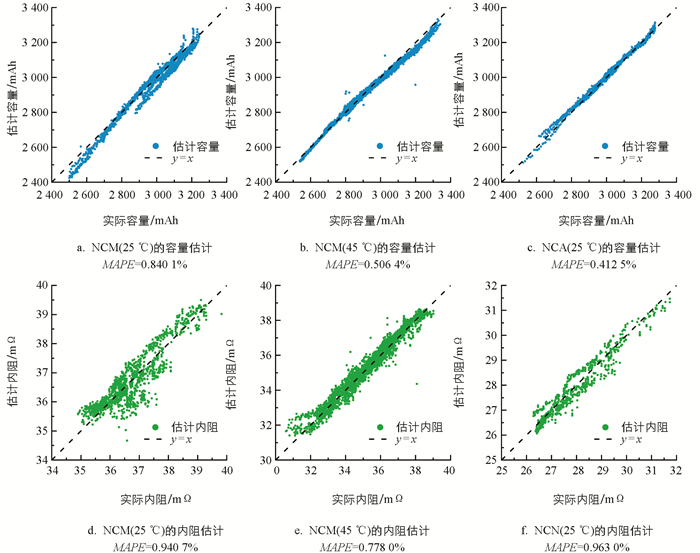
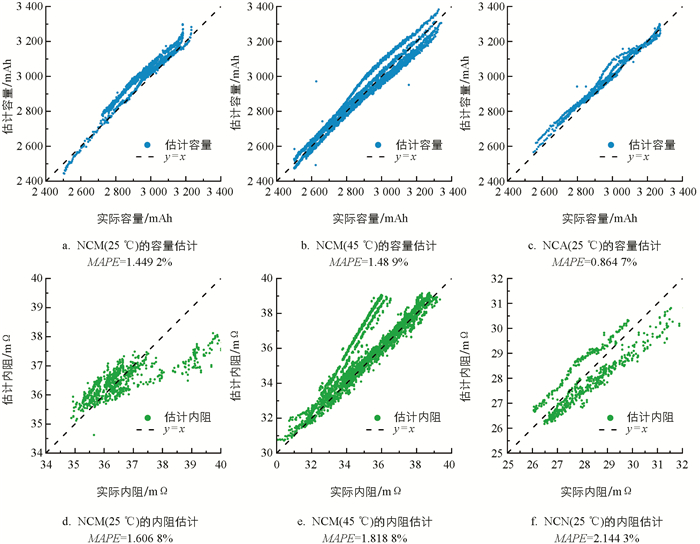
将建立的模型在前文所述3类电池上分别验证,以4∶1的比例按电池单体编号随机划分训练集和验证集. 由于不同电池单体之间存在差异,为了降低数据划分的随机性对模型估计精度的影响,实验重复进行了10次随机分组,记录每次的模型估计结果,以稳健地评估模型性能. 模型10次随机分组的容量和内阻估计RMSE和MAPE的均值、最佳情况和最差情况分别如表 2和表 3所示. 分析表 2和表 3可见,模型在NCM(25 ℃)、NCM(45 ℃)和NCA(25 ℃)3类电池的容量和内阻估计上均取得了较高的估计精度,容量估计的平均MAPE分别为1.055%,0.832%和0.610%,内阻估计的平均MAPE分别为1.238%,0.946%和1.512%. 在10次随机分组的最差情况中,容量估计MAPE均小于1.5%,内阻估计MAPE均小于2.2%. 为了直观地展示随机分组的最佳情况和最差情况,图 4和图 5分别展示了对应的可视化结果. 模型估计结果证明了本文建立的弹性网络模型可以在相同特征输入的情况下,实现高精度的锂离子电池容量和内阻估计,且有良好的鲁棒性.
-
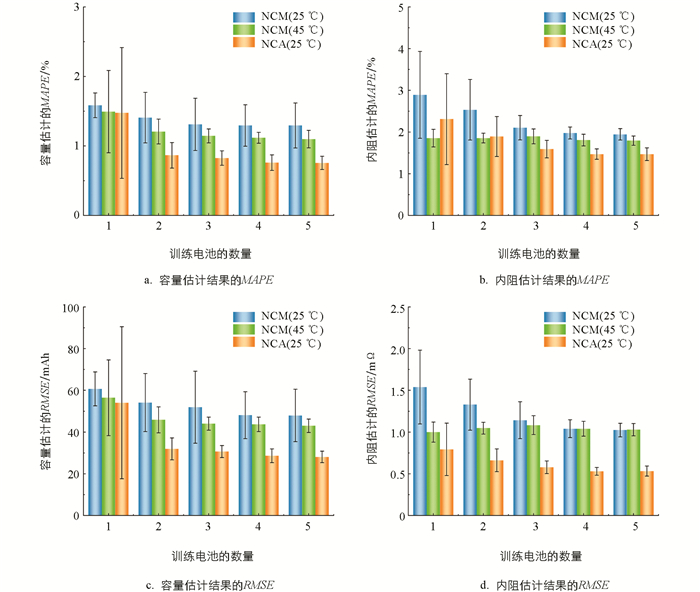
在实际应用中,由于成本限制,通常希望使用尽可能少的训练数据实现精确地建模. 因此本节探讨了模型在训练数据量较小的情况下,模型的容量和内阻估计精度. 对于每一种类型的电池,任取5个电池作为验证集,在验证集不变的前提下,逐渐扩大训练数据的规模,即依次随机取1个、2个、…、5个电池作为训练集,分析模型精度随训练样本规模增大的变化. 为了避免随机抽样对结果的影响,实验重复进行了10次.
图 6展示了模型的估计精度随训练样本数增加的变化. 在仅有1个电池做训练样本时,模型容量和内阻估计结果的标准差较大,说明抽样的随机性对模型影响较大. 这是由于训练集和验证集的数据分布不均造成的. 而随着参与模型训练的电池数量的增加,容量和内阻估计的MAPE及其标准差均在降低. 总体而言,对于每一种材料体系和温度工况的电池,仅需2个电池的实验数据用作模型训练,就可以保证容量估计的误差在2%以内,内阻估计的误差在3%以内,证明了本文建立的模型对训练样本数的需求量不大,可以有效地降低基于数据驱动建模的数据收集成本,对实际工程应用有一定参考价值.
4.1. 评价指标
4.2. 模型精度验证
4.3. 模型在小样本训练下的估计结果
-
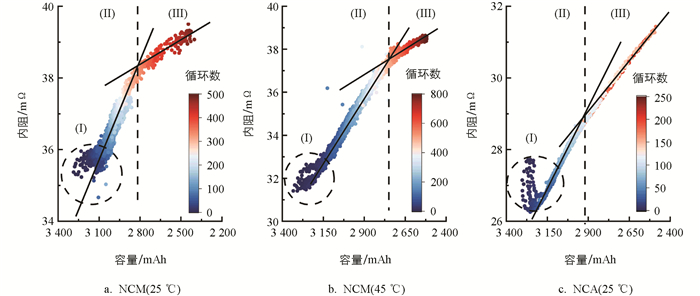
在建立的容量和内阻协同估计模型的基础上,本文提出了基于容量和内阻双参量的“三段式”电池评价方法,从而在两个维度评价电池的不一致性. 图 7展示了前文所述3种电池随着循环次数的增加,其容量衰减和内阻增加的散点图. 由图 7可知,电池的容量衰减和内阻增加随循环数的变化并非单一的线性关系,而且可以分成3个部分:区域(I)处于电池衰减初期,电池容量和内阻的相关性相对较弱,容量和内阻两维度的信息可以帮助在电池衰减初期进行更合理的电池分选;在电池老化的全生命周期中,还存在一个拐点将容量—内阻曲线分为(II)和(III)两个斜率明显不同的部分,说明在分界点附近电池的衰减机理发生了变化,导致电池的热力学和动力性特性的变化速率也随之改变. 电池容量和内阻双参量的“三段式”分析表明,以往仅通过单一的电池容量参数来评价电池性能是片面的,需要引入基于容量和内阻的双参量评价方法,从能量特性和功率特性两方面更全面地评估电池系统性能.
-
为了准确估计锂离子电池的容量和内阻,本文提出了一种基于数据驱动和弹性网络算法的电池容量和内阻估计方法,可以在相同特征输入下实现高精度的容量和内阻协同估计,且在小样本训练时仍保持较高的估计精度. 从电池恒流充电至4.0 V到4.2 V电压区间的充电片段提取容量增量(IC)特征,经过重采样过程重构特征向量,训练弹性网络模型. 使用KIT数据集中3种不同材料体系和温度工况的电池进行验证. 研究结果表明,使用相同的输入特征,模型的容量估计误差在1%左右,内阻估计误差在1.5%左右,证明了本文模型在容量和内阻估计方面的优越性;并且模型在小样本训练(仅使用2个电池训练模型)时,可以保证容量估计的误差在2%以内,内阻估计的误差在3%以内,从而大大降低电池数据驱动建模的数据收集成本. 最后,本文提出了基于容量和内阻双参量的“三段式”电池评价方法,可以从两个维度更全面地评价电池系统性能.



 下载:
下载: