Singer模型认为，机动模型是相关噪声模型，而不是通常假定的白噪声模型.对目标加速度a(t)作为具有指数自相关的零均值随机过程建模^[7]，即：

其中σ_m²和α是在区间[t，t+τ]内决定目标机动特性的待定参数：σ_m²是目标的加速度方差，α是机动时间常数的倒数，即机动频率.

对于机动加速度方差σ_m²，通常假设机动加速度的分布为：

(1) 机动加速度等于极大值a_max的概率为p_M，等于－a_max的概率也为p_M；

(2) 机动加速度等于极大值0的概率为p₀(非机动概率)；

(3) 机动加速度在区间[－a_max，a_max]上近似服从均匀分布.

由此假定，可得概率密度函数为

式中：1(.)是单位阶跃函数；δ(.)是狄拉克脉冲函数.由(2)式可得噪声方差为

则Singer模型的状态方程可以表示为

其中：

噪声协方差为：

Singer模型中参数α和σ_m²的确定依赖于先验知识，且一旦确定，在滤波过程中不再变化.因此，当事先确定的参数α和σ_m²与实际情况有较大差别时，滤波精度会变得较低.为了弥补Singer模型这一缺点，文献[2]提出了一种参数自适应调整的Singer模型滤波算法.它依据目标机动的可能等级，设定多组相应的参数α和σ_m²；在滤波过程中依据加速度的滤波值，确定目标在当前时刻的机动等级，并设置Singer模型在当前时刻对应的参数α和σ_m²，从而在之后的跟踪过程中使用新的状态方程滤波.

具体过程为：

1) 依据机动等级，事先设定N组参数α和σ_m².可以计算出相应的状态矩阵F(k，α)和过程噪声协方差Q(α，σ_m²).

2) 依据当前时刻卡尔曼滤波器输出的加速度估计值$\mathop a\limits^ \wedge $(k|k)，选择合适的参数α和σ_m²：

① 若a_i－1，max < $\mathop a\limits^ \wedge $(k|k) < a_i，max，则选择α=α_i，σ_m²=σ_m，i²；

② 若$\mathop a\limits^ \wedge $(k|k) < a_1，max，则选择α=α₁，σ_m²=σ_m，1²；

③ 若$\mathop a\limits^ \wedge $(k|k)>a_N，max，则选择α=α_N，σ_m²=σ_m，N².

3) 计算F(k，α)和Q(α，σ_m²)，并进行滤波.

这种参数自适应调整的Singer模型算法，所需的运算量与原Singer模型相同，但跟踪效果大大提升.然而，这种自适应调整算法是依赖于事先设定的N组机动参数，参数的设定有较大的主观性.此外，这种参数调整方法是离散的，当隶属度发生变化时，会造成参数调整的突变，从而可能会带来较大的误差.因此，本研究试图找到一种连续调整Singer模型参数的方法.

α是Singer模型的机动频率参数，一般认为大气扰动时机动频率参数α=1，机动频率参数α=1/60，表示慢速转弯机动；机动频率参数α=1/20，表示逃避机动^[8].机动频率参数α取值越大，过程噪声协方差Q越大.

由Singer模型状态方程可知，加速度方差与过程噪声协方差阵成正比.而Singer模型的最大加速度a_max与加速度方差也是正相关.因此，当a_max越大，则过程噪声协方差Q越大，而当a_max越小，则过程噪声协方差Q越小.因此，当目标发生强机动时，最大加速度a_max取较大的值，滤波误差较小，效果较好.当目标弱机动时，最大加速度a_max取较小的值，滤波平滑的效果比较好.

增加过程噪声协方差阵Q，相应的滤波增益矩阵也会增大，进而加大了系统的校正权值，越能适应强机动；减小过程噪声协方差阵Q，相应的滤波增益矩阵也会减小，进而减小了系统的校正权值，此时对弱机动目标的跟踪效果更好.因此，可以通过实时改变a_max，达到调整滤波效果的目的.

IMM算法^[9]滤波过程中，每个时刻所有模型并行地进行滤波.模型的似然函数用来表示当前滤波模型的可能性：

式中：v_kⁱ为第i个模型在k时刻滤波的残差，S_kⁱ为第i个模型在k时刻滤波的残差协方差.其中，归一化的新息平方ε_k=(v_kⁱ)′(S_kⁱ)^－1v_kⁱ作为目标机动检测的变量被广泛使用.

由(9)式可以看出，似然函数是新息的函数，且新息越大，似然函数取值越小，表明模型可能性越小.因此，考虑用模型的似然函数作为目标机动检测的变量.

如果把Singer模型取不同的参数当作是不同的滤波模型，则当时间常数及其他几个参数确定时，可以把Singer模型取不同的最大加速度a_max看作是不同的模型.如果把最大加速度a_max与模型似然函数联系起来，那么就找到了基于似然函数变化的自适应Singer模型算法.

具体地，假设第一个时刻，初始似然函数为：

假设初始时刻的最大加速度为a_0，max，则第k个时刻对应的似然函数为：

使用模型的似然函数来实时更新最大加速度a_max，可以表示为：

将k时刻的最大加速度a_k，max，带入Singer模型滤波公式中，求得状态转移矩阵F和过程噪声矩阵Q，通过卡尔曼滤波公式实时更新滤波状态值.

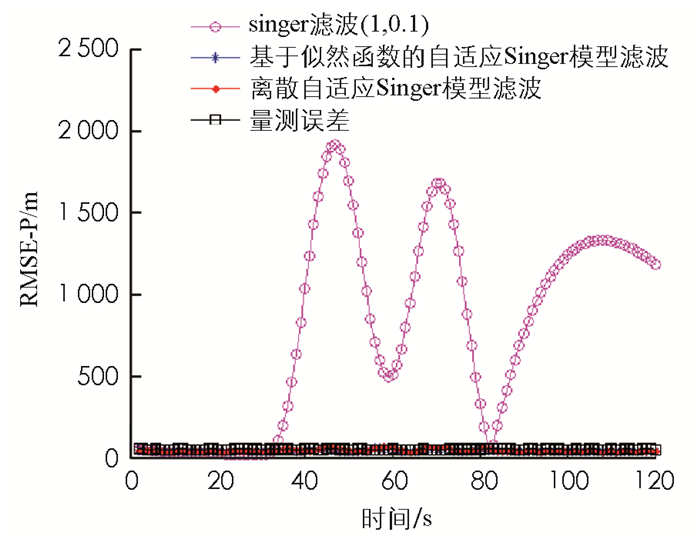
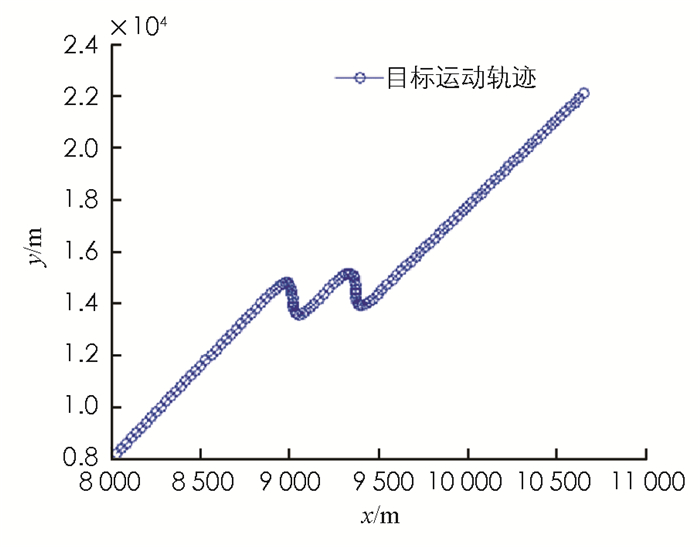
假设采样周期是T=1 s，目标的初始状态是X₀=[x，${\dot x}$x，${\ddot x}$，y，${\dot y}$，${\ddot y}$，z，${\dot z}$，${\ddot z}$]^T，其中X₀=[8 000，28，0，8 000，200，0，10 000，0，0]^T，其中位置的单位是m，速度单位是m/s，加速度单位是m/s²；目标先做直线运动，然后以角速度为15°/s做2个S转弯机动，最后做直线运动. 3个方向的量测噪声都为均值是50 m的高斯白噪声，得到目标运动轨迹(图 1).

蒙特卡洛仿真100次，分别计算Singer模型算法取不同参数及两种自适应Singer模型滤波算法的位置均方根误差，分别画出算法的滤波位置均方根误差(RMSE-P)曲线(图 2).

由图 2可以看出，当Singer模型的参数取α=1，a_max=0.1时，模型参数与目标的机动不匹配，目标发生机动时，Singer模型的滤波误差非常大.

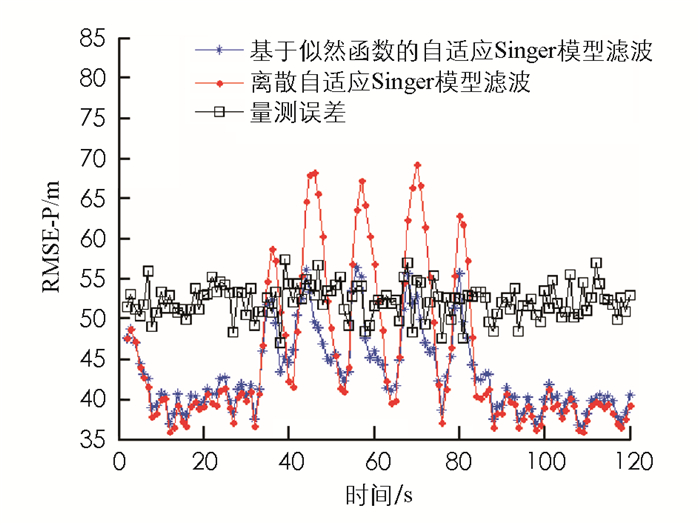
画出基于似然函数的自适应Singer模型滤波及离散自适应Singer模型滤波的位置均方根误差(RMSE-P)曲线(图 3).由图 3可以看出，模型参数基于似然函数调整的自适应Singer模型滤波算法在目标机动时误差较小，参数离散调整的Singer模型滤波算法在目标机动时误差比较大.这是因为离散调整的Singer模型算法当模型的隶属度变化时，会引起参数的突变，以致带来较大的误差.

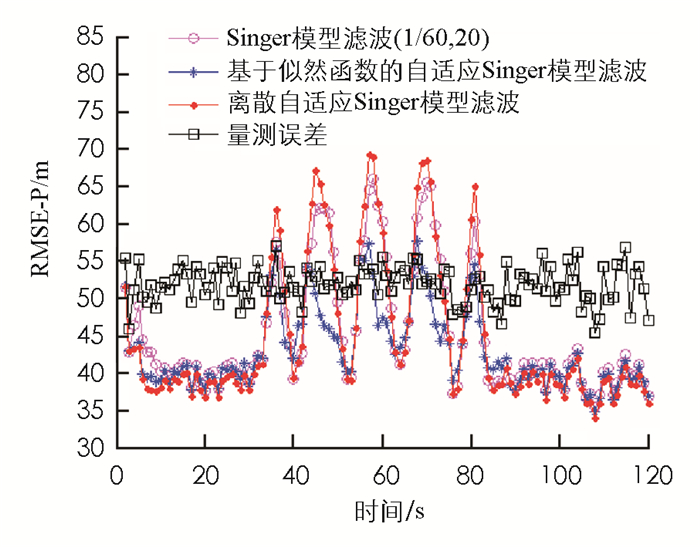
如图 4所示，Singer模型的参数取α=1/60，a_max=20时，因为Singer模型的参数更能适应目标机动，Singer滤波误差小，滤波效果较优于离散自适应Singer模型算法.总体而言，参数基于似然函数调整的Singer模型滤波误差最小，滤波效果最好.

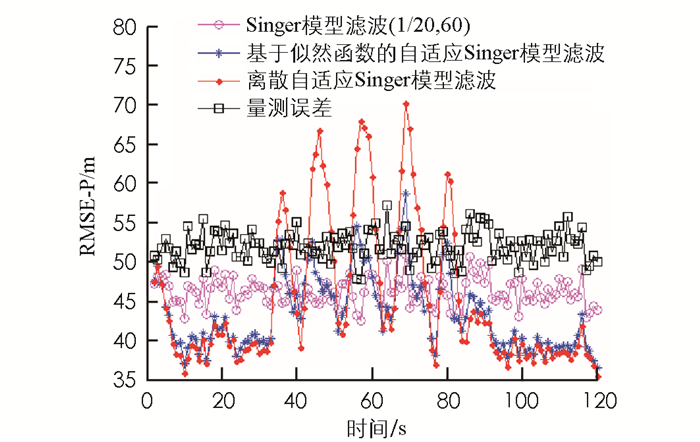
如图 5所示，Singer模型的参数取α=1/20，a_max=60时，因为Singer模型的参数与目标的机动匹配，因此目标机动时滤波误差最小，滤波效果优于两种自适应算法.但是，目标在直线运动阶段，Singer模型滤波位置均方根误差(RMSE-P)最大，效果最差.

对传统Singer模型滤波算法及本文提到的两种自适应算法进行时效性分析.所有的结果统一在CPU：英特尔酷睿I7-7500U，内存为4 GB的计算机上进行100次蒙特卡洛仿真，对比3种算法运行时间得到的结果见表 1.

通过仿真结果可以看出，Singer模型滤波选择不同的模型参数时，滤波效果差异较大.本文提到的两种自适应算法由于没有改变模型的复杂度及模型个数，因此计算量与时效性都与Singer模型相当.当目标机动时，基于似然函数调整的Singer模型滤波效果更好，而离散调整的Singer模型算法当模型的隶属度变化时，引起参数的突变，会带来较大的误差.当目标没有机动时，两种自适应算法效果相近.总体而言，基于似然函数的自适应Singer模型算法性能最稳定，效果最好.

实际中，往往不能提前预知目标的机动情况，而Singer模型的参数一旦确定，在滤波过程中便不能更改.因此，单一参数的Singer模型难以适应不同的机动类型^[10].本文提出了一种基于模型似然函数的自适应Singer模型.通过仿真验证，这种基于似然函数的自适应Singer模型滤波算法能有效跟踪目标不同的机动段.滤波效果比离散自适应Singer模型算法^[5]更好，更能适应目标的机动.