PT5是将(x_i，Y_i)的多标记示例经过一定的处理后形成|Y_i|个单标记数据集，比如，(x₁，{y₁，y₂})可以转换成(x₁，y₁)和(x₁，y₂)2个单标记示例，接着分配一个单标记分类器给上述各个数据集.同时，所有的单标记分类器都会有一个对应的分布，表示每个对象属于相应类别的概率，并根据分布为每个对象输出一组类标记集合.通常情况下取threshold=0.5为最低阈值.进行类别y_l包含示例x_i的概率预测时，如果该数值大于最低阈值，则将类别y_l合并到示例x_i预测类别集合.公式表示形式为

在PT5方法中，为其设置一个适当的最低阈值对该方法非常重要，在现有的多标记学习算法中设置一个适合的最低阈值也十分必要.阈值设置得过高或过低都会影响到预测结果.当我们设置的阈值过高时，得到的预测结果就可能不全；当我们设置的阈值过低时，就会得到大量的无用类别.因此，在所有的类别中设置同一个阈值是不恰当的.

为解决设置最低阈值的难题，基于最低阈值多目标学习，本文提出了TFEL学习算法.在使用该算法时，对于类别y_l(1≤l≤|Y|)，都将会有一个阈值与之对应，在本文中将其记为threshold_l，同时所有类别的标记集合记为Y.如果一个示例x_i预测为类别y_l，可能性f (x_i，y_l) > threshold_l，将其代入式(2)，并将y_l的类别标记添加到对x_i预测的类别标记集合中，即

TFEL方法对传统单标记学习算法和现有多标记算法中的阈值确定具有通用性.

对于多标记学习中如何设置适合的最低阈值，本文提出了一种新的学习算法——基于最低阈值的多标记学习算法(TFEL，Threshold For Each Label).

TFEL方法通过对训练数据集学习，根据标记学习为每个类别得到一个阈值.

在TFEL算法中，首先对训练数据集进行训练得到每个类别y_l的概率f (x_i，y_l).然后将f (x_i，y_l)存储在相应集合中，如式(3)、式(4)所示.再对概率f (x_i，y_l)进行学习，为每个标记y_l得一个最低阈值.

在上式中，对于类别y_l中所有示例的数据集记为D_l⁺；对于D_l⁺示例中属于y_l的概率f(x_i，y_l)的集合记为Λ_l⁺.同理，对于类别y_l中所有示例的数据集记为D_l^－；对于D_l^－示例中属于y_l的概率f(x_i，y_l)的集合记为Λ_l^－.如式(5)和式(6)所示，其分别属于Λ_l⁺中的最小值与最大值区间和Λ_l^－中的最小值与最大值区间.

在上式中，由集合Λ_l⁺中的最小概率Λ_Minl⁺和最大概率Λ_Maxl⁺构成的区间记为Ξ_l⁺.同理，由集合Λ_l^－中的最小概率Λ_Minl^－和最大概率Λ_Maxl^－构成的区间记为Ξ_l^－.

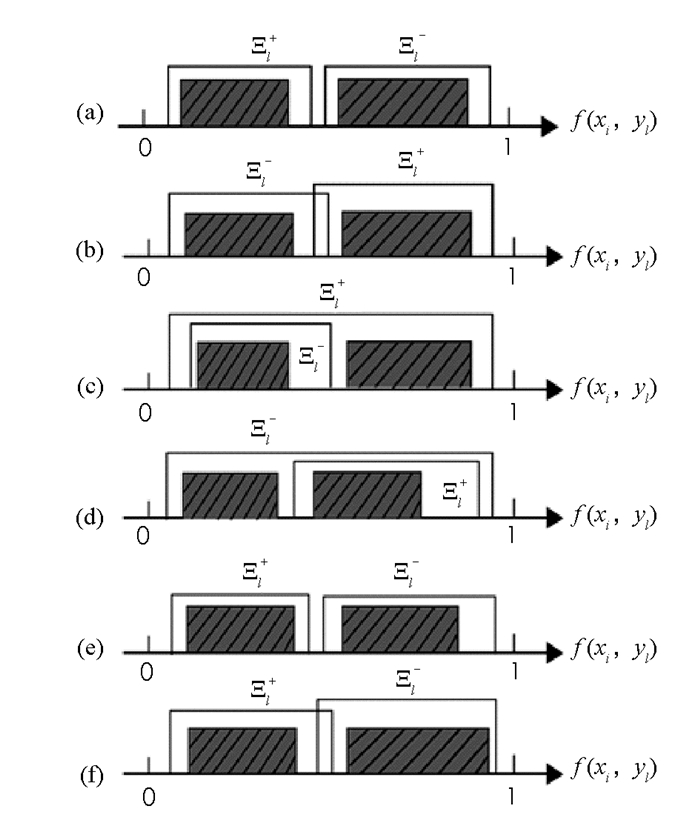
如图 1所示，区间Ξ_l⁺和Ξ_l^－存在6种位置关系. 图 1(a)表示所有正例比负例被预测为y_l的概率f (x_i，y_l)都高，图 1表示的是最理想状态. 2个区间有交集的情况如图 1(b)-图 1(d)所示，最常见的情况如图 1(b)所示.正确的可能性大小和f (x_i，y_l)存在的位置有关系，对于一个测试示例，当其被预测为类别y_l的f(x_i，y_l)值位于交集中时，那么预测结果很有可能是错误的.当其被预测为类别y_l的f (x_i，y_l)值位于交集两侧时，那么预测结果很有可能是正确的.其他情况如图 1(e)-图 1(f)所示，在训练集中对于本应该属于类别y_l的示例，其被预测为不属于类别y_l的概率要比预测为属于类别y_l的概率要大，可以看出该分类器性能较差.

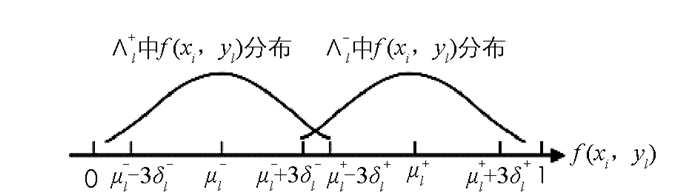
由最大值Λ_Maxl^±和最小值Λ_Minl^±可以确定区间，从图 1(a)-图 1(f)中的阴影部分可以看出，Λ_l⁺和Λ_l^－中的分值集中分布在某一段区间上.通过χ²拟合度检验得知，Λ_l⁺和Λ_l^－集合中的值f(x_i，y_l)均近似服从正态分布，如图 2所示.

确定正态分布中的参数μ和参数δ是求解TFEL方法中最低阈值的前提.因此，求得参数μ和δ的准确值对阈值确定很关键.本文根据无偏估计法求出其近似值，求解方法如式(7)和式(8)所示.

对Λ_l⁺中所有概率值求标准差和均值，分别记为$ \hat{\delta }_{l}^{+}$和$ \hat{u }_{l}^{+} $.同理，对Λ_l^－中所有概率值求标准差和均值，分别记为$ \hat{\delta }_{l}^{-} $和$ \hat{u }_{l}^{-} $.由正态分布图中的3δ标准可知，阈值threshold_l可能会有以下3种：

式9-式10中参数均利用式7-式8中计算得到的估计值.

TFEL算法伪码的实现过程如下：

In：

集合D用于表示多标记数据集的集合，则有D={(x₁，Y₁)，(x₂，Y₂)，…，(x_|D|，Y_|D|)}；

集合Y表示所有类别标记的集合，则有Y={y₁，y₂，…，y_|Y|}；

f(，)：计算概率的函数；

thrType：阈值类型(Min_l，Max_l，Mid_l)以及i的值；

t：测试示例；

Out：f_TFEL(t)对测试示例t预测的类别标记集合.

Process：

1) 计算Λ_l⁺和Λ_l^－-，1≤l≤|Y|；

2) 根据式7-式8计算u_i，δ_i，u_l^±和δ_l^±，1≤l≤|Y|；

3) 根据上一步计算得到的结果和给定的thrType计算threshold_l，1≤l≤|Y|；

4) $ {{f}_{TFEL}}(t)=\underset{{{y}_{l}}\in Y}{\mathop{\cup }}\, \{{{y}_{l}}\}:f(t, {{y}_{l}})>\text{threshol}{{\text{d}}_{l}} $

多标记学习算法常用的评估标准有Hamming Loss，Average Precision，Average Precision，Coverage和α-Evaluation等.本文选取2个最适合的评估标准Hamming Loss和α-Evaluation.

根据Hamming Loss评估标准，用计算器分类器可以得出对象预测出的类别标记集合和实际对应的类别标记集合差异个数. D为多标记数据集，M表示数据集中对象的总数，f(x)为多标记分类器，x_i为测试数据对象，Y_i为x_i对应的类标记集合，该评估标准可表示为式(12)所示.

其中，f(x_i)ΔY_i=(f(x_i)－Y_i)(Y_i－f(x_i)). Hamming loss的值越小说明分类器的性能越好，反之则差.

假定多标记数据集D，类标记集合Y={y₁，y₂，…，y_L}，示例x_i对应的类标记集合为Y_i，分类器得到的类标记集合为P_i.没有预测到的类标记集合用M_i=Y_i-P_i表示；预测的错误类标记集合用F_i=P_i-Y_i表示.

其中，参数α≥0，β≥0，γ≤1，β=1|γ=1，该值越大，表明分类器的性能越好.

为验证TFEL算法的有效性，从UCI下载数据集iris和diabetes.这2个数据集中均存在属性相同，而对应类别标记不相同的示例.实验中将这些属性相同，对应类别标记不相同的示例类别标记预处理成他们所属多个类别标记的集合.例如，存在示例(x₁，y₁)，(x₁，y₂)和(x₁，y₃)，则将示例的类别标记预处理成{ y₁，y₂，y₃}，即(x₁，{y₁，y₂，y₃}).预处理后的数据集信息如表 1所示.

为了方便获得一个示例属于每个类别标记的概率f(x_i，y_l)，基于贝叶斯算法对分类模型进行建模.为确定阈值大小对分类结果的影响，本文根据TFEL和朴素贝叶斯算法，为每个类别设置一个最低阈值，同时为每个类别标记选取9组值.将i取1，2和3分别代入公式(9)和公式(10)中，threshold_l产生3组不同的取值(Min_l，Max_l和Mid_l)，然后通过TFEL方法对测试数据集进行分类.设定β和γ参数的取值均为1，通过Hamming Loss和α-Evaluation评估标准对分类结果进行评估.

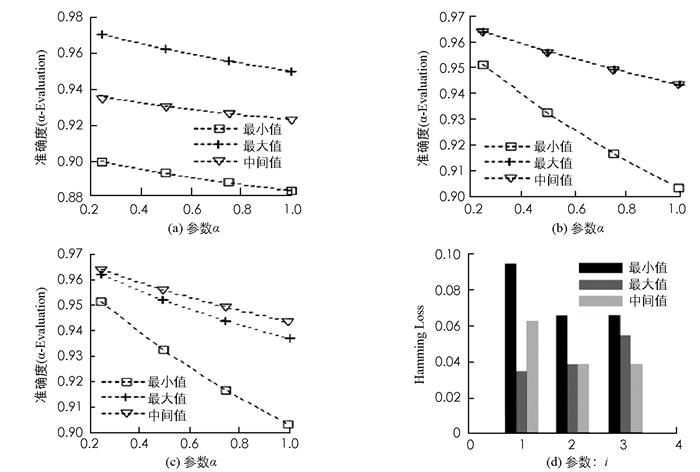
利用TFEL方法对数据集iris分类后的评估结果如图 3所示.

其中，图 3(a)、图 3(b)和图 3(c)分别是式9-式10中参数i取1，2和3时的分类结果，图 3(d)是当i取不同值时，对Hamming loss评估值的比较.通过对比图 3(a)-图 3(d)得出，当threshold_l和Max_l相等时，分类器性能达到最佳，当i=1时，准确率达到最高，Hamming loss评估值达到最低.

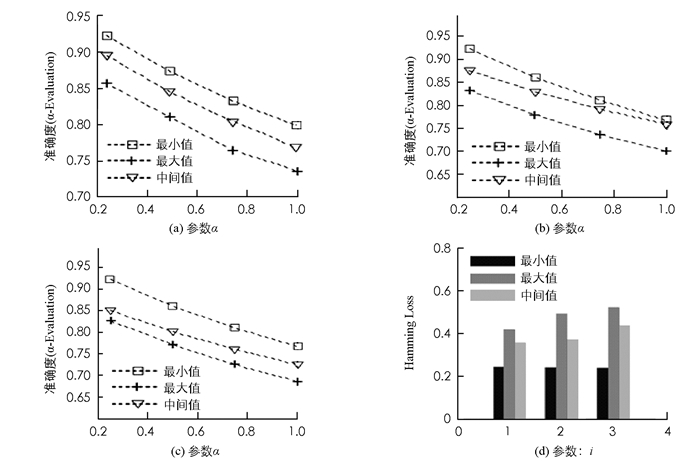
为了确定当阈值threshold_l = Max_l时，是否对每个数据集分类器都能得到最佳性能，实验利用TFEL方法对diabetes数据集进行分类，分类后的评估结果如图 4所示.

其中，图 4(a)、图 4(b)和图 4(c)分别是式9-式10中的参数i取1，2和3时的分类结果，当threshold_l=Min_l时，分类器的准确率均高于其他2组取值. 图 4(d)中，当threshold_l=Min_i时，Hamming loss评估值均小于其他2组评估值.通过总结图 4(a)-图 4(d)得出，当分类器对diabetes数据集的整体分类性能达到最优时，threshold_l=Min_l.

实验结果表明，TFEL方法能有效的对多标记数据集进行分类，同时对于不同的数据集，在取不同的阈值时，分类器都可以表现出良好的性能.

通过对多标记学习详细的理论研究，本文结合最低阈值知识提出了多标记学习TFEL算法.通过训练数据集可以得到每一个类别标记的最佳最低阈值，这样能够使分类器的分类性能达到最佳.通过对该算法进行大量实验，结果表明TFEL算法具有较好的分类效果.但本文算法也具有一定的不足，后续工作需要：①对单标记数据进行预处理得到数据集，将TFEL方法应用于现有的多标记数据集；②将TFEL方法中的阈值确定方法应用于现有的多标记学习算法，并进行分析比较；③进一步研究数据集中每一个类别正负例个数的分布对最低阈值的影响.