-
裂缝多孔介质中流体流动的建模已成为一个重要问题.在多孔介质中常出现两种类型的裂缝[1-2].降维模型可以模拟两种类型的裂缝,并允许穿过裂缝界面的压力不连续.其数值方法[3-10]已被广泛应用于裂缝多孔介质中的流体流动模型.
本文第1节简要描述了简化模型的推导;第2节用块中心有限差分方法对该模型进行离散,并给出一些相应的记号;第3节通过数值实验来证明块中心有限差分法求解该模型的有效性,证明了裂缝是快速通道还是地质屏障主要取决于裂缝处渗透率张量的大小.
全文HTML
-
设Ω是
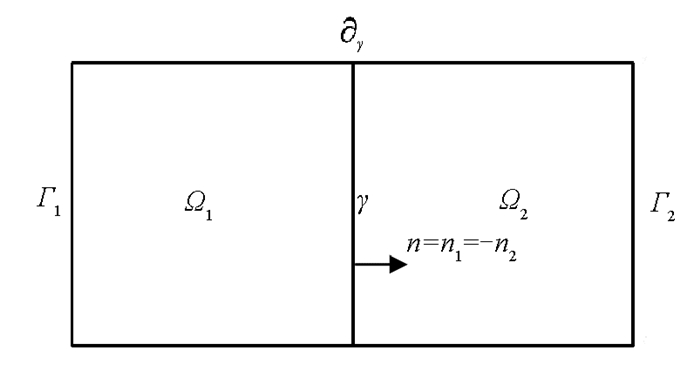
${{\mathbb{R}}^{n}} $ 中的凸域,n=2或3,定义Γ=∂Ω是Ω的边界.设在Ω中的流动遵循质量守恒和达西定律:其中:p是压强,u是达西速度,K是渗透率张量(K是对角的,且里面的元素都非零),q是源项,pb是在边界Γ上给定的压强.假设在多孔介质Ω中存在单一的裂缝Ωf将Ω分为3个连续的子区域(图 1),其中:d表示裂缝的宽度;Γi表示位于Γ上Ωi的部分边界,i=1,2,f;Γi=∂Ωi∩Γ;γi表示裂缝Ωf和Ωi的共同边界部分;γi=∂Ωi∩∂Ωf∩Ω,i=1,2;ni表示γi的单法向量.如果用pi,ui,Ki和qi分别表示p,u,K和q对Ωi的限制,i=1,2,f,pbi表示pb在边界Γi上的限制,则式(1)可以写成如下形式:
通过传统的非重叠域分解方法求解式(2)时,Ωf可以简单视为Ω的一个子域并在Ωf处进行局部细化.
将Ωf视为Ω1和Ω2之间的一个界面,来模拟裂缝就不需要对裂缝处的网格进行局部细化,并且在裂缝处只需处理(n-1)维的非线性问题,而不需要求解原来n维的问题(图 2).
通过对裂缝处进行平均处理建立了用界面代替子域的模型.首先分解裂缝处的速度
${{\mathit{\boldsymbol{u}}}_{f}}={{\mathit{\boldsymbol{u}}}_{f, n}}+{{\mathit{\boldsymbol{u}}}_{f, \tau }} $ ,其中$ \boldsymbol{u}_{f, n}=\left(\boldsymbol{u}_{f} \cdot \boldsymbol{n}\right) \boldsymbol{n}\left(\boldsymbol{n}=\boldsymbol{n}_{1}=-\boldsymbol{n}_{2}\right)$ 并定义$ {{\nabla }_{\tau }}$ 和divτ分别为切线方向的梯度算子和散度算子,$ {{\nabla }_{n}}$ 和divn为法线方向的梯度算子和散度算子.所以式(2)的第一个方程可写为对式(3)在法线方向积分有
其中:
$ U_{f}=\int_{-d / 2}^{d / 2} \boldsymbol{u}_{f, \tau} {\rm{d}} \boldsymbol{n}, Q_{f}=\int_{-d / 2}^{d / 2} q_{f} {\rm{d}} \boldsymbol{n}$ .根据流体通过γ1和γ2的连续性条件(式(2)中最后一个方程),可以把式(4)写成如下形式:这是关于γ的守恒方程,其中
$ {{\mathit{\boldsymbol{u}}}_{1}}\cdot {{\left. {{\mathit{\boldsymbol{n}}}_{1}} \right|}_{{{\gamma }_{1}}}}+{{\mathit{\boldsymbol{u}}}_{2}}\cdot {{\left. {{\mathit{\boldsymbol{u}}}_{2}} \right|}_{{{\gamma }_{2}}}}$ 是附加的源项,代表在裂缝中流入和流出的差异.对于式(2)的第二个方程可以写成:然后对式(6)的第一个方程在法线方向积分有
其中
$P_{f}=\frac{1}{d} \int_{-d / 2}^{d / 2} p_{f} {\rm{d}} \boldsymbol{n}, d $ 表示原模型裂缝的宽度(通过积分产生).式(7)是(n-1)维γ上的达西定律.现在对式(6)的第二个方程给出系统Ω1和Ω2沿γ处的边界条件,其考虑了从γ的一侧到另一侧的压力差.对第二个方程在法线方向积分有:用梯形公式进行近似有:
令
$\alpha_{f}=2 K_{f, n} / d $ ,将(9)式写成如下形式:则图 2中满足的守恒方程和达西定律如下:
其中:第3个方程表示沿裂缝切线方向的达西定律;第4个方程模拟了裂缝内部的质量守恒;第5个方程表示子域Ωi的Robin边界条件[11],与裂缝中的压强pf和相邻子域Ωj中的流通量有关i,j=1,2,i≠j.当ξ取不同值时,原模型可简化为不同的问题,特别地当ξ=1时模型问题简化为非局部[12]非标准正定界面问题,并且当ξ∈[1/2,1]时第5个方程可以写成:
降维模型式(11)可以在不损失裂缝介质的物理性质的情况下降低计算成本.
-
考虑在一个矩形区域Ω=[a,b]×[c,d]内,被裂缝Ωf={xf}×[c,d]分为两个子区域[13-15]Ω1=[a,xf)×[c,d]和Ω2=(xf,b]×[c,d].对于一维裂缝,有如下划分:
二维区域Ω1和Ω2分别划分为δ1x×δy和δ2x×δy:
令
$s=1, \cdots, N_{x}, l=1, \cdots, N_{y} $ ,定义如下记号:对于函数ψ(x,y)定义ψi,j为ψ(xi,yj),其中i可以取值s或者s+1/2,j可以取值l或者l+1/2.在适当点处的离散形式如下:
其中h和k分别为x方向和y方向的步长.在裂缝中
$ u_{1, \hat{N} x+1 / 2, l}^{x}$ 和$u^{x}_{2, \hat{N} x+1 / 2, l} $ 的值一般是不相等的.运用上面的记号,用$u_{i, s+1/2, l}^{x}, u_{i, s, l+1/2}^{y}, \quad {{p}_{i, s, l}}, {{u}_{f, \hat{N}x+1/2, l+1/2}}, \quad {{p}_{f, \hat{N}x+1/2, l}} $ 来近似$u_{i}^{x}\left( {{x}_{s+1/2}}, {{y}_{l}} \right), u_{i}^{y}\left( {{x}_{s}}, {{y}_{l+1/2}} \right), $ ${{p}_{i}}\left( {{x}_{s}}, {{y}_{l}} \right), {{u}_{f}}\left( {{x}_{\hat{N}x+1/2}}, {{y}_{l+1/2}} \right), {{p}_{f}}\left( {{x}_{\hat{N}x+1/2}}, {{y}_{l+1/2}} \right) $ 其中i=1,2,则方程(11)可以写成如下形式:(14) 式加上边界条件就可以构成一个封闭的系统.在(14)式中我们需要利用裂缝周围介质的压力来构造有限差分格式,但是它们又不是在裂缝处上定义的,所以需要用插值来近似
$ {{p}_{1, \hat{N}x+1/2, l}}$ 和${{p}_{2, \hat{N}x+1/2, l}} $ 的值.很显然该差分方法具有二阶的精度.
-
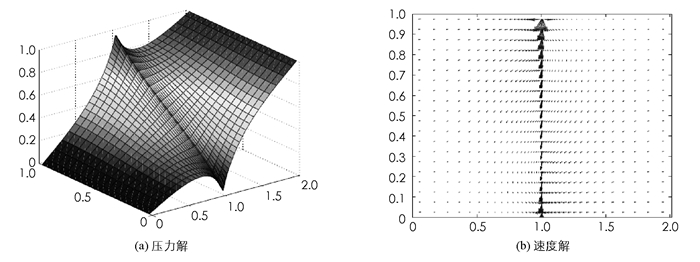
例1 如图 3所示,裂缝划分的两个区域分别为Ω1=[0,1-d/2]×[0, 1],Ω2=[1+d/2,2]×[0, 1].在裂缝处的渗透率为Kf=KI,在其它区域的渗透率是各向同性的常数:K1= K2= I.裂缝的宽度为d,源项为0,qi=0,i=1,2,f.在裂缝处给出第一类边界条件,其中I是二维的单位矩阵,K是一个大于1的参数.这意味着,流体快速通过裂缝.
图 4为裂缝处局部细化的网格结果(K=100,d=0.01),图 5为降维模型块中心有限差分的数值结果(K=100,d=0.01,ξ=2/3).
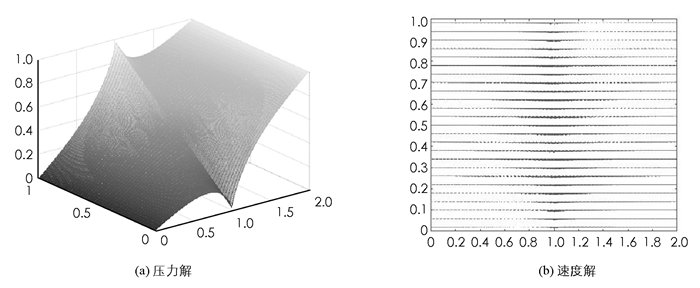
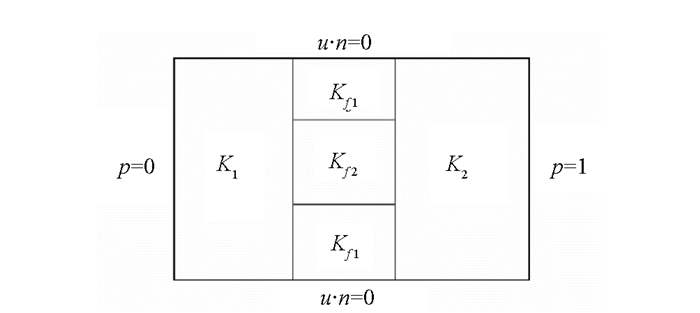
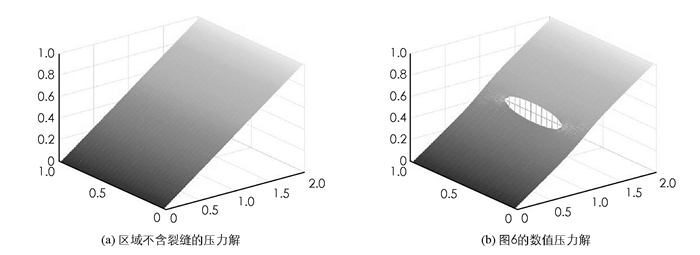
例2 如图 6所示,考虑裂缝在{1}×([0,1/4]∪[3/4,4])处的渗透率为Kf1=KfI,Kf=200,在{1}×[1/4,3/4]处的渗透率为Kf2=KfI,其中Kf=0.001在周围基质的渗透率与上一个例子一样,在裂缝边界处给的是第二类边界条件如图 6.用块中心有限差分方法离散降维模型并近似求解了压力图像,如图 7所示(其中d=0.01,ξ=2/3).
-
本文主要用块中心有限差分方法来模拟二维裂缝多孔介质中单相达西流动问题,用一维界面来描述裂缝,并与周围介质进行流体交换.通过数值算例验证了该方法的有效性.数值实验表明裂缝是否作为快速通道或地质屏障取决于裂缝处渗透率张量的大小.




 下载:
下载: