本文中，所有环都是具有单位元的结合环，所有的模均是酉模.R-gr表示所有分次左R-模构成的范畴.令M和N是分次左R-模.我们用Hom_R-gr(M，N)={f：f ∈Hom_R(M，N)且f(M_σ)⊆N_σ，σ∈G}表示R-gr中从M到N的所有态射.如果对所有σ∈G，f(M_σ)⊆N_στ，则称R-线性映射f：M→N是度为τ的分次态射，其中τ∈G.度为τ的分次态射构成了Hom_R(M，N)的加法子群HOM_R(M，N)_τ.易知HOM_R(M，N)_e=Hom_R-gr(M，N).故Hom_R(M，N)=⊕_τ∈GHOM_R(M，N)_τ是分次阿贝尔群.对任意的i＞0，我们用Ext_Rⁱ(M，N)，Ext_R-grⁱ(M，N)，EXT_Rⁱ(M，N)分别表示Hom_R(M，N)，Hom_R-gr(M，N)和HOM_R(M，N)的右导出函子.

设M是分次右R-模，N是分次左R-模. M与N的分次张量积为M⊗_RN=⊕_σ∈G(M⊗_RN)_σ，其中x⊗_Ry∈(M⊗_RN)_σ(x∈M_α，y∈N_β)且αβ=σ.我们用Tor_i^R(M，N)表示M⊗_RN的左导出函子.设M是分次右R-模，M⁺=HOM_$\mathbb{Z}$(M，$\mathbb{Q}$/$\mathbb{Z}$)表示M的分次示性模.

文中未解释的概念和符号，请参见文献[4-9].

定义1^[4]   R-gr中的平坦对象称为平坦分次模. R-gr中的内射对象称为分次内射模.

定义2  ^[3]如果在R-gr中存在分次平坦左R-模的正合列…→F₁→F₀→F⁰→F¹→…，使得$M \cong {\rm{Ker}}$(F⁰→F¹)，且对任意分次内射右R-模I，I⊗_R-作用序列正合，则称M是Gorenstein分次平坦模.

定义3^[2]  设x是R-gr的子范畴.令0→A→B→C→0是R-gr中的短正合列.

(ⅰ)如果A和C在x中，有B也在x中，则称x关于扩张封闭；

(ⅱ)如果B和C在x中，有A也在x中，则称x关于满同态的核封闭；

(ⅲ)如果x满足以下3条，则称x是投射可解类：

(a) x包含所有分次投射左R-模；

(b) x关于扩张封闭；

(c) x关于满同态的核封闭.

定义4  如果gr-$\mathscr{G}$$\mathscr{F}$(R)关于扩张封闭，则称分次环R是左分次GF-封闭环，其中gr-$\mathscr{G}$$\mathscr{F}$(R)表示所有Gorenstein分次平坦左R-模组成的类.我们可以类似地定义右分次GF-封闭环.

引理1  对分次左R-模，以下结论等价：

(ⅰ) M是Gorenstein分次平坦模；

(ⅱ) M满足以下两条：

(a) 对任意的i>0及任意的分次内射右R-模I，Tor_i^R(I，M) =0；

(b) 在R-gr中存在分次左R-模的正合序列0→M→F⁰→F¹→…，其中Fⁱ是分次平坦模，且对任意分次内射右R-模I，I⊗_R-作用序列正合.

(ⅲ)在R-gr中存在分次左R-模的短正合列0→M→F→G→0，其中F是分次平坦模，G是Gorenstein分次平坦模.

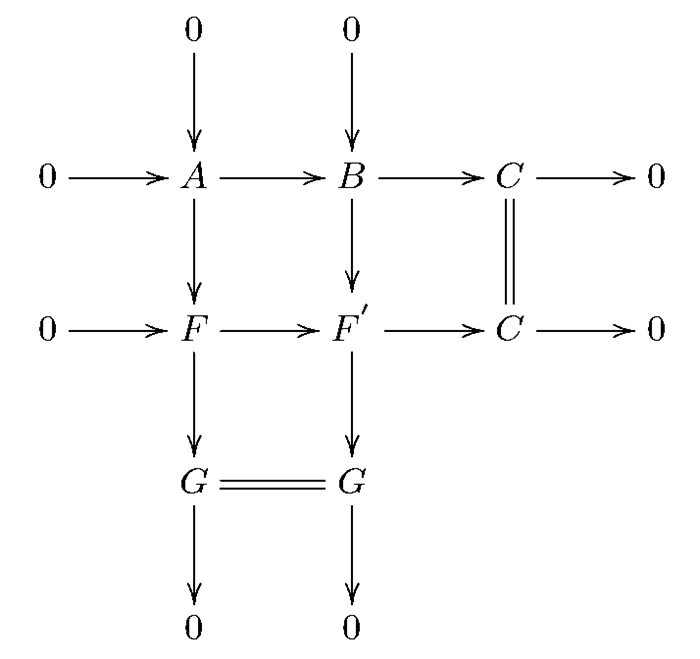
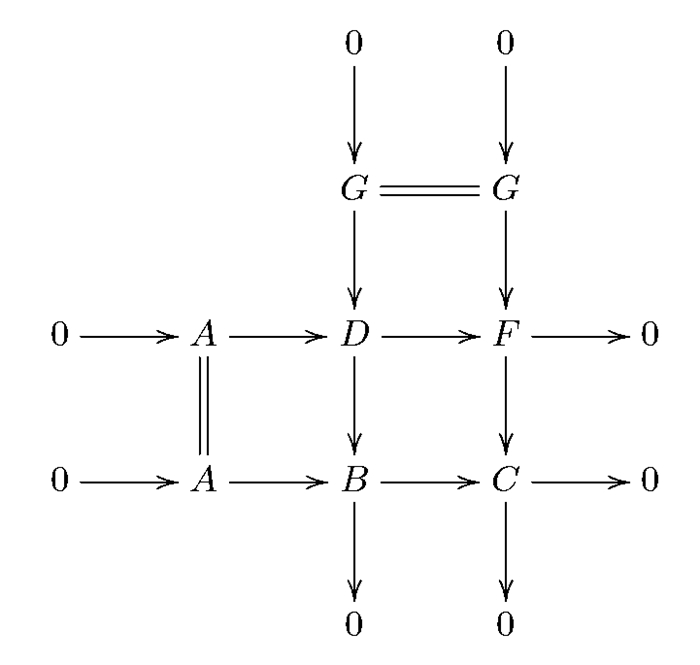
证  (ⅰ)⇒(ⅱ)因为M是Gorenstein分次平坦模，所以在R-gr中存在分次左R-模的正合序列…→F₁→F₀→M→0，其中每个F_i是分次平坦模.令${L_n} \cong {\rm{ker}}$(F_n-1→F_n-2)，L₀=M，且对任意分次内射右R-模I，I⊗_R-作用序列正合.考虑短正合列0→L₁→F₀→M→0，我们得到如下交换图(图 1).

由分解引理知，Tor₁^R(I，M)=0.当i>0时，由长正合序列

得${\mathop{\rm Tor}\nolimits} _2^R(I, M) \cong {\mathop{\rm Tor}\nolimits} _1^R\left({I, {L_1}} \right)$.利用数学归纳法得到对任意i>0，有Tor_i^R(I，M)=0.

由(ⅰ)，在R-gr上也存在分次左R-模的正合序列0→M→F⁰→F¹…，其中Fⁱ是分次平坦模，且对任意分次内射右R-模I，I⊗_R-作用序列正合.

(ⅱ)⇒(ⅰ)因为M存在分次平坦分解…→F₁→F₀→M→0，其中每个F_i是分次平坦模，且对任意分次内射右R-模I，Tor_i^R(I，M)=0，则I⊗_R-作用序列正合.将M的平坦分解与(ⅱ)中正合列首尾相接，便得R-gr上分次平坦左R-模的正合列$\mathbb{F}$：…→F₁→F₀→F⁰→F¹→…，使得$M \cong {\rm{Ker}}$(F⁰→F¹)，其中F_i，Fⁱ是分次平坦模，且对任意分次内射右R-模I，I⊗_R$\mathbb{F}$作用序列正合.因此，M是Gorenstein分次平坦模.

(ⅰ)⇒(ⅲ)显然.

(ⅲ)⇒(ⅱ)设在R-gr中存在分次左R-模的短正合列

其中F是分次平坦模，G是Gorenstein分次平坦模.设I是分次内射右R-模，因为G是Gorenstein分次平坦模，所以对任意的i≥0，由长正合列

得到Tor_i^R(I，M)=0.

因为G是Gorenstein分次平坦模，所以存在分次左R-模的正合序列

其中Fⁱ是分次平坦模，且对任意分次内射右R-模I，I⊗_R-作用序列正合.把序列(1)和(2)连接起来，得到序列0→M→F→F⁰→F¹→…，且对任意分次内射右R-模I，I⊗_R-作用序列正合.

引理2  设0→A→B→C→0是R-gr中分次左R-模的短正合序列.如果A是Gorenstein分次平坦模，C是分次平坦模，那么B是Gorenstein分次平坦模.

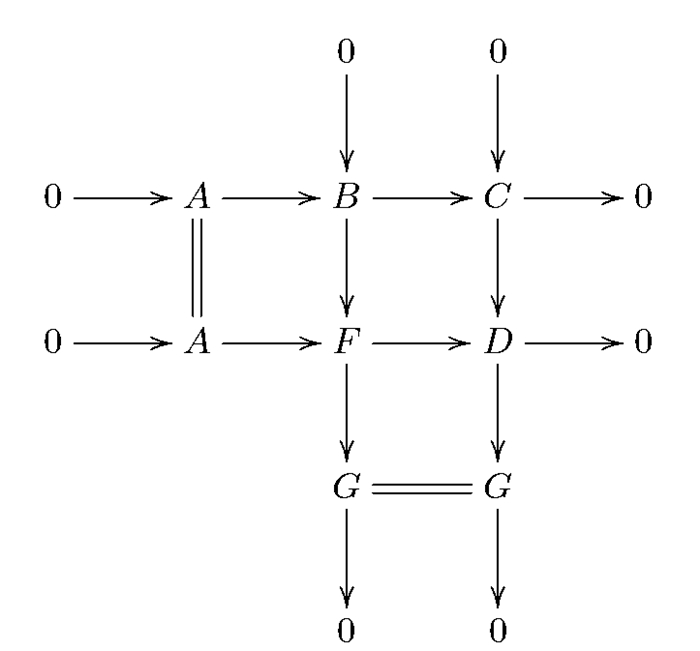
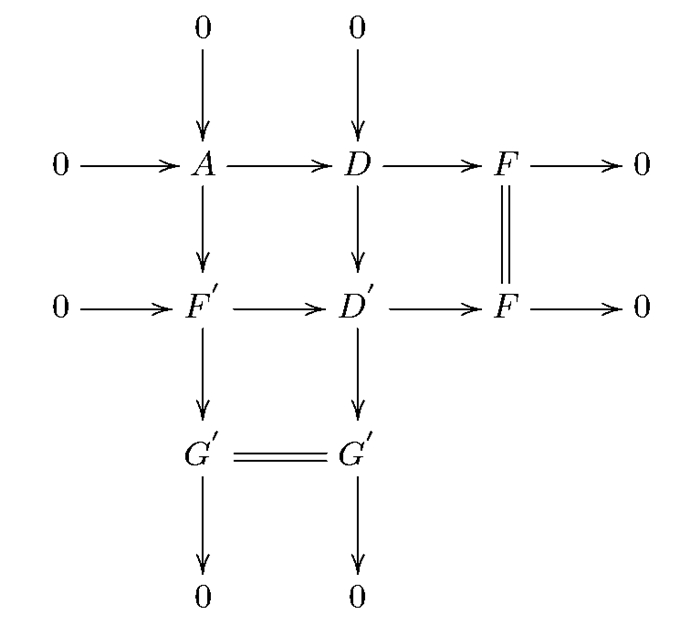
证  因为A是Gorenstein分次平坦模，所以在R-gr中存在分次左R-模的正合序列0→A→F→G→0，其中F是分次平坦模，G是Gorenstein分次平坦模.考虑A→B和A→F的推出，如图 2所示.

在短正合列0→F→F′→C→0中，因为F和C是分次平坦模，所以F′也是分次平坦模.

在短正合列0→B→F′→G→0中，因为F′是分次平坦模，所以由引理1得，B是Goren-stein分次平坦模.

定理1  对分次环R，以下结论等价：

(ⅰ) R是左分次GF-封闭环；

(ⅱ) gr-GF(R)是投射可解类；

(ⅲ)对R-gr分次左R-模短正合列0→G₁→G₀→M→0，其中G₁，G₀是Goren-stein分次平坦模.如果对任意分次内射右R-模I，有Tor₁^R(I，M)=0，那么M是Gorenstein分次平坦模.

证  (ⅰ)⇒(ⅱ)考虑分次左R-模的短正合列0→A→B→C→0，其中B和C是Gorenstein分次平坦模，下面证明A是Gorenstein分次平坦模.因为B是Gorenstein分次平坦模，则在R-gr中存在分次左R-模的短正合列0→B→F→G→0，其中F是分次平坦模，G是Gorenstein分次平坦模.考虑B→C和B→F的推出，如图 3所示. 图 3右侧垂直短正合列中，C和G是Gorenstein分次平坦模.因为R是左分次GF-封闭环，所以D是Gorenstein分次平坦模.因此由中间水平短正合列及引理2知，A是Gorenstein分次平坦模.

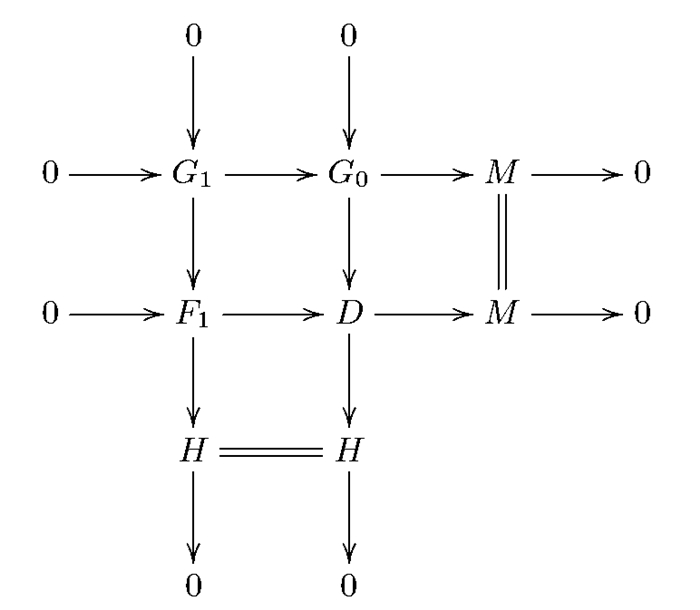
(ⅰ)⇒(ⅲ)因为G₁是Gorenstein分次平坦模，所以在R-gr中存在分次左R-模的短正合列0→G₁→F₁→H→0，其中F₁是分次平坦模，H是Gorenstein分次平坦模.考虑G₁→F₁和G₁→G₀的推出，如图 4所示. 图 4右侧垂直短正合列中，G₀和H是Gorenstein分次平坦模.因为R是左分次GF-封闭环，所以D是Gorenstein分次平坦模.因此在R-gr中存在分次左R-模的短正合列0→D→F→G→0，其中F是分次平坦模，G是Gorenstein分次平坦模.

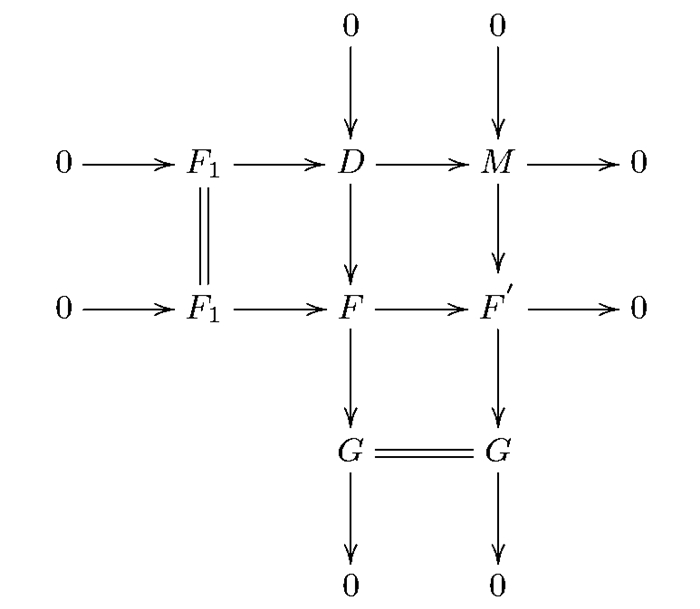
考虑D→F和D→M的推出，如图 5所示.下面证明F′是分次平坦模.考虑短正合列0→M→F′→G→0.设I是分次内射右R-模.由长正合序列

我们得到Tor₁^R(I，F′)=0.

考虑短正合序列0→F₁→F→F′→0.得短正合列0→(F′)⁺→F⁺→(F₁)⁺→0.因为F和F₁是分次平坦左R-模，所以由文献[10]的引理2.1和定理3.5知，F⁺和(F₁)⁺是分次内射右R-模.由Tor₁^R(I，F′)=0及文献[11]的引理2.1得

因此序列0→(F′)⁺→F⁺→(F₁)⁺→0可裂.故(F′)⁺是分次内射右R-模F⁺的直和项，所以(F′)⁺是分次内射右R-模.由文献[10]的引理2.1和定理3.5知，F′是分次平坦左R-模.在短正合列0→M→F′→G→0中，由引理1知，M是Gorenstein分次平坦模.

(ⅲ)⇒(ⅰ)考虑R-gr中分次左R-模的短正合列0→A→B→C→0，其中A和C是Gorenstein分次平坦模，下面证明B是Gorenstein分次平坦模.设I是分次内射右R-模.用I⊗_R-作用短正合列0→A→B→C→0，得到长正合序列

因为A和C是Gorenstein分次平坦模，所以由引理2知，对任意的i>0，有Tor_i^R(I，B)=0.因为C是Gorenstein分次平坦模，所以在R-gr中存在分次左R-模的短正合列0→G→F→C→0，其中F是分次平坦模，G是Gorenstein分次平坦模.考虑F→C和B→C的拉回，如图 6所示.因为A是Gorenstein分次平坦模，所以在R-gr中存在分次左R-模的短正合列0→A→F′→G′→0，其中F′是分次平坦模，G′是Gorenstein分次平坦模.

考虑A→F′和A→D的拉回，如图 7所示. 图 7中间水平短正合列中，因为F′和F是分次平坦模，所以D是分次平坦模.由右侧垂直短正合列及引理2知，D是Gorenstein分次平坦模.最后，我们考虑短正合列0→G→D→B→0.因为G和D是Gorenstein分次平坦模，且对任意的i>0及任意的分次内射右R-模I，Tor₁^R(I，M)=0.所以由(ⅲ)知，B是Gorenstein分次平坦模.故R是GF-封闭环.

推论1  设R是左分次GF-封闭环，那么gr-$\mathscr{G}$$\mathscr{F}$(R)关于分次直和项封闭.

证  因为gr-$\mathscr{G}$$\mathscr{F}$(R)是投射可解类，所以由文献[12]的命题1.4知，只需说明gr-$\mathscr{G}$$\mathscr{F}$(R-)关于分次直和封闭即可.由文献[3]的推论2.11知结论成立.