北斗卫星导航系统主要包括地面控制中心、客户端、导航通信卫星3个方面，地面控制中心由校正站、计算中心、测轨站、测高站和主控站构成，实现卫星定位导航参数的校正及测量，对卫星运行姿态及轨道进行调控，编制星历，对用户定位修正资料及实现用户定位.该系统35颗卫星在离地面2万多公里的高空上，以固定的周期绕地球运行，使得任意时刻在地面上的任意位置都可以同时观测4颗以上的卫星.由于卫星的位置精确可知，通过接收机对卫星进行观测，测得卫星至接收机的距离.考虑到卫星时钟与接收机时钟之间的误差，卫星定位时有4个未知数，观测点的位置X，Y，Z和钟差.利用距离公式，观测4颗卫星，就可以组成4个方程式，解出观测点的位置，进而实现卫星定位.俄罗斯研发的GLONASS系统因为研发维护经费问题，现代实用性及前景并不良好.欧洲GALILEO系统还处于试验阶段，也并不是成熟导航系统^[3].所以，本文将北斗卫星导航系统和现代使用率较高的美国GPS实现对比，见表 1.

和美国GPS相比，北斗卫星导航系统毫不逊色，是具备快速定位、精密授时、短报文通信等特点的全球卫星导航定位系统，能够使有无自主导航系统问题进行解决，还能够在国土资源等关键部门推广使用.

北斗卫星导航系统定位技术是利用空间距离后方交会方法，对空间点三维位置进行确定.接收机接收卫星发射的电磁波信号，得到时间差或者相位差，与电磁波传播速度或波长相结合，通过计算得到卫星至接收机的距离.因为存在误差，所以计算距离值并不真实，也就是伪距^[4].

因为已知电磁波传播速度，所以测码伪距观测量就是北斗卫星发射信号到用户接收机接收信号的传播时间τ.如果不考虑钟差，将传播误差等影响忽略，那么北斗导航卫星到用户接收机天线的几何距离计算公式为

在卫星系统的设计过程中，卫星钟和接收机钟使用两种不同的时间基准，那么卫星信号发射时间和接收机接收信号时间具有时间偏差.为了对问题进行说明，进行以下变量的定义：

t^s(sat)：将星钟作为时间基准的卫星信号发射时间；

t_r(rec)：将站钟作为时间基准的卫星信号接收时间；

t^s：卫星发射信号时刻的北斗时间真值；

t_r：接收机接收信号时刻的北斗时间真值；

δt^s：星钟钟差；

δt_r：站钟钟差；

Δt：不考虑传播误差影响，星钟时间卫星发射信号和站钟时间接收机接收信号传播时间^[5].

根据上述定义，那么

假如卫星到观测站的几何距离设置为Rrs，伪距为prs，那么得到

如果对误差进行考虑，那么观测历元t时刻的测码伪距观测方程

R_r^s(t)是观测历元t时刻所观测的卫星到接收机天线的几何距离；δt_r^s是观测历元t时刻接收机钟差和卫星钟差的综合影响；Δ_r，I^s是观测历元t时刻电离层对测码伪码的影响，Δ_r，T^s是对流层折射对于测码伪距的影响. M是伪距多路径效应，e指测量噪声^[6].

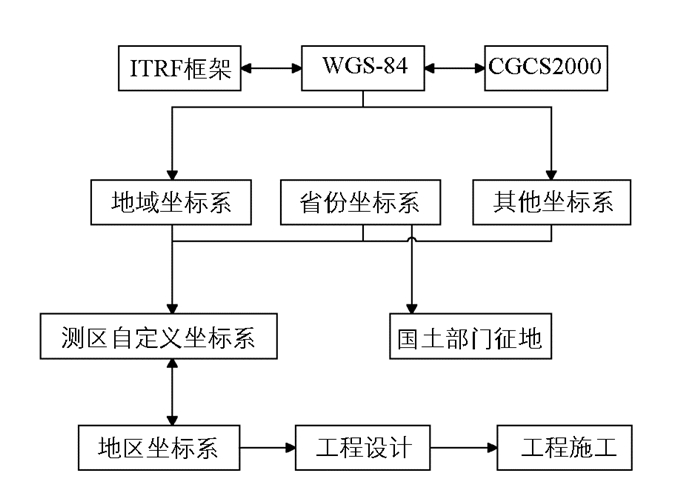
在土地测绘过程中涉及坐标系包括我国大地坐标系、世界大地坐标系、独立坐标系及地方城市坐标系4种.因为我国坐标系在不断地完善，以不同的用途使4大类坐标系又划分为8种类型，图 1为土地测绘坐标系.

WGS-84为基于ITRF2000框架中的1997历元坐标，CGCS2000属于ITRF97框架中2000历元坐标，目前我国很多测量成果使用ITRF2008框架.若要实现WGS-84坐标或CGCS2000坐标转换至ITRF2008框架坐标，就需要坐标转换.假设ITRF_B属于转换之前的框架，ITRD_A为转换之后的框架，P(t_B)指的是转变之前的历元，P(t_A)指的是转换之后的历元^[7]，则可用Helmert转换模型，那么就有以下转换方程

上述转换方程未知转换参数的数量一共有14个，假如已知5个以上的公共点，不仅能够得到转换参数，创建关系，还能够实现任意框架及历元之间的相互转换.

用户接收机接收北斗卫星导航系统信号，能够得到3个载波频率相位观测值，对3个频率的相位观测值实现线性组合，以此得到组合观测值为

上述公式中i，j，k是任意的整数，f₁，f₂，f₃是北斗系统的载波频率.

组合中相位观测值精度表示为

其中，σϕ是相位观测值的精度，R(i，j，k)是组合载波观测值噪声放大因子.结合北斗3个频率观测值，创建具备长波特性的宽巷、超宽巷组合，从而固定模糊度^[8]. 表 2为两种北斗宽巷的载波组合.

通过两个超宽巷组合模糊度对宽巷模糊度在土地测绘过程进行求解，基线一般都比较短，对延迟的情况进行求解，双差观测方程为

将已经固定的模糊度Δ▽N(0，-1，1)的超宽巷相位观测值和宽巷相位观测值创建几何模型，即

宽巷模糊度的精度为

假如双差载波噪声σ_Δ▽ϕ=0.005 m，对以上公式进行分析，表示模糊度的解为99.9%，也就是宽巷模糊度能够固定单历元^[9].

坐标系属于工作基础，全部测量成果都是将其作为基础，所以坐标系的选择和工程质量具有密切的关系.平面控制测量中，地面长度投影到参考椭球面，再将椭球面长度投影到高斯平面均会引起长度变形.当长度变形不大于2.5 cm/km时，可直接采用高斯正形投影的国家统一3°带平面直角坐标系.此项目首级控制四等卫星定位控制点坐标反算和实地测量相邻点边长之差满足规范要求，高程归化和高斯投影距离改正综合影响小于2.5 cm/km.以如下公式实现验证计算.

其中，ΔD表示地面水平距离投影到椭球面的长度变形，D表示地面水平距离，H表示边长两端点的平均大地高程，R表示平均曲率半径.

假设平均曲率半径设置为6 371 km，归化高程设置为50~2 000 m，椭球体中的边长S投影到高斯平面中，长度也会有变形，设为△S，假设此边2个端点平均坐标为y_m，坐标差为△y，那么

由于$\frac{{{{(\Delta y)}^2}}}{{24{R^2}}}$项很小，趋于0，公式(15)可近似表达为

公式(14)、公式(16)计算出的ΔD、ΔS之和即为检验长度变形是否超限的验证依据.由两公式可以得出只有工程坐标系满足以下条件，才能够被使用：

1) 工程范围在正形高斯投影3°分带中央子午线附近；

2) 工程范围平均高程和国家水准面接近；

3) 使用已知控制点高于首级控制点^[10].

对测区内各边长进行检验，若不能够满足长度变形小于2.5 cm/km，需采用假定坐标系，以确保精度需求得到满足^[11-12].

结合测区每条边两端点的平均大地高和平均y坐标，对照表 3内容，计算结果为长度变形均小于2.5 cm/km，表明该测区国家统一3°带平面直角坐标系能够满足土地测绘需求，在实地测量过程中不需要建立假定坐标系.

以项目需求，为了使验算精度结果得到保证，使用全站仪对可通视边长进行测量，并且将仪器常数改正、投影改正、倾斜改正及气象改正相互结合.全站仪的技术指标为

1) 往返观测测回数≥2；

2) 边长一侧回读数之间的较差限差≤2 mm；

3) 垂直角观测测回数≥2；

4) 边长测回之间的较差≤3 mm^[13].

通过表 4可以看出，土地测绘四等卫星定位控制点反算边长与全站仪实际测量边长的差都在12.2 mm以下，利用较差计算相对误差，最大值为1/11.2万，均比《工程测量规范》四等导线测距相对中误差限差1/8万要小.以此表示本次测量坐标系的使用精准，也表示了本次工程首级控制网成果较为可靠^[14-15].

本文对北斗卫星导航系统特点和功能进行了分析，该系统属于全新监测系统，能够保证土地测绘的精准性，将其在地理测绘中使用，具有良好的实用性效果.北斗卫星导航系统的应用范围较广、稳定性较高，能够使土地资源测绘管理水平得到提高，在实时测绘过程中，能够为地理测绘提供重要的参考信息，经济价值较高.