为准确识别机器人的避障，我们需要建立针对机器人避障路径的观测模型，以分析机器人的运动状态^[9-10].机器人在运动时，其位置和姿态角在全局坐标系中用$ {\mathit{\boldsymbol{x}}_r} = {\left( {x,y,\phi } \right)^T}$表示.其中，(x，y)为机器人的具体位置；$\phi $为机器人纵轴与全局坐标系纵轴的夹角，$\phi $的方向设置中，一般是将全局坐标系纵轴设定为0°，沿逆时针方向为正，顺时针方向为负，故姿态角$\phi $的范围为-180°~180°.若某一个较短时间间隔为ΔT，机器人运动速度为V_t，偏转角度为α_t，则机器人在此时间段里的运动距离是V_t·ΔT.在这种情况下，机器人的运动模式可利用基于控制命令的运动模型表示，在输入u_t=(V_tα_t)时，对机器人运动情况进行分析的结果如下所示：

其中，x_t，y_t为机器人在空间坐标系中的坐标；${{\phi }_{t}} $为机器人的朝向角；ΔT是采样时长；R是机器人的两轮中心间隔；σ_v是机器人的速度噪声；σ_y是机器人旋转时的角度噪声.

假设观测到的环境特征是静止的，且其模型可用点特征表示.在全局坐标系中，环境特征i的位置S_i=(x_i，y_i)，其中i=1，2，…，k是环境特征个数.如上所述，假设机器人的环境特征为静止，因而采用测距传感器可获取第i个环境特征和机器人间的距离r_i，以及与机器人的相对角度θ_i.则机器人的观测模型g(s_t，λ_nt)可表示为：

其中，v(t)为噪声协方差矩阵；(x_i，y_i)为第i个环境特征在空间坐标系中的坐标；(x_t，y_t)为机器人在空间坐标系中的坐标；r_i为机器人的位置与第i个路标的间距，θ_i为相对角度；σ_d为观测模型的距离噪声；σ_θ为观测模型的角度噪声；X′为机器人位置X_t与第i个环境特征在空间坐标系中的坐标联合状态向量；$\nabla g\left( \centerdot \right)$为观测模型对于机器人位置X_t与第i个环境特征的坐标联合状态向量X′的Jacobian矩阵，可表示为：

其中，

基于粒子滤波(Particle Filter，PF)的SLAM方法是将移动机器人的观测模型融入PF中，通过随机采样点表示状态向量的后验概率密度函数.但在高维状态空间中进行采样时，需要用大量的样本来保障算法的性能，而计算复杂度将随样本数量的增多显著增大.因此，本文采用基于RBPF的SLAM方法进行降噪滤波处理. RBPF的基本思路可用下式表示：

其中，t为采样时间；s^t={s₀，s₁，…，s_t}为机器人的位置集合；u^t-1={u₀，u₁，…，u_t-1}为机器人的控制输入信息集合；z^t={z₀，z₁，…，z_t}为机器人的观测数据集合；λ_t=λ₁，λ₂，…，λ_t为观测的环境特征集合；$\lambda _{t}^{k}=\left( \lambda _{1}^{k}, \lambda _{2}^{k}, \cdots, \lambda _{t}^{k} \right) $为t时刻机器人观测到的第k个环境信息；n^t为数据关联参数.

首先，对机器人避障路径信息进行调整，将采样前的机器人避障路径信息集设置为$\left\{ S_{i}^{t} \right\}=\left\{ S_{i}^{t}, W_{i}^{t} \right\}, i=1, 2, \cdots, M $其中，$S_{i}^{t} $为预测采样时机器人位置状态的后验概率分布，对应的权重是$W_{i}^{t} $.在进行重采样时，需要针对机器人避障路径信息集$S_{i}^{t} $重新计算避障路径信息分布，则避障路径选择速度及位置的更新公式如下所示：

其中，$V_{i}^{t} $为避障路径信息$ S_{i}^{t}$采集时在t时刻的速度；$ S_{i}^{t}$为避障路径信息i在t时刻的位置；S_pbest为机器人位置值的局部最优解；S_gbest为机器人位置值的全局最优解；ω为惯性权重算子；r₁，r₂为时间均匀分布的随机数；c₁和c₂为加速算子.为确保算法一直处于最优收敛速度，ω需要满足以下条件：

其次，我们对避障路径信息进行选择.在经过重新计算之后，避障路径信息集变为

按权重大小进行排列，并从避障路径次数中选择次数最少的路径信息，以$ \left\{ S_{i}^{t+1}, W_{i}^{t+1} \right\}$进行表示.其中，$W_{i}^{t+1}$为避障路径信息$S_{i}^{t+1} $对应的权值.在引入适应度函数Fit(·)和能效吸引力F_i，k对避障路径信息进行选择时，结果如下所示：

其中，${{F}_{i, k}}=Fit\left( {{s}_{i}} \right)-Fit\left( {{s}_{k}} \right), Fit\left( {{s}_{i}} \right)=W_{i}^{t}, Fit\left( {{s}_{k}} \right)=W_{k}^{t}, {{F}_{i, k}} $为避障路径信息i对避障路径信息k的能效吸引力.

最后，我们对选取的避障路径信息进行滤波，降低周围环境对避障路径信息的干扰，实现对避障路径的预处理.设置滤波时的随机线性离散时间系统表达式为：

其中，X_k是n维状态向量；y_k是m维观测序列，Φ_k是n×n维状态转移矩阵；Γ_k是n×p维的输入噪声矩阵；H_k是m×n维的观测矩阵；U_k是p维噪声序列；V_k是m维观测噪声序列.此时的初始估计误差协方差矩阵为

其中，X₀为避障路径初始状态，${{\overset{\wedge }{\mathop{X}}\, }_{0}} $为初始状态的估计值.经H_∞滤波后，结果如下所示

上式中p₀为对称正定阵，表示初始估计值${{\overset{\wedge }{\mathop{X}}\, }_{0}} $和初始状态X₀间偏差的大小.

综上所述，通过建立机器人观测模型，并对避障路径信息重采样后进行H_∞滤波，可降低周围环境对避障路径信息的干扰，实现对避障路径的预处理，从而为机器人最优避障路径的识别提供基础依据.

在对路径信息进行滤波的基础上，依据适应度函数对机器人避障路径进行排序，并通过视觉分析法按排序结果依次识别，选出最优避障路径.换言之，在对避障路径进行滤波的基础上，主要以适应度函数为避障路径选取准确度的标准，进行避障路径排序.

假设避障路径上路标点p_i的绝对坐标为(x_i，y_i)，i=1，2，…，n，起始点坐标为(x₀，y₀)，目标点绝对坐标为(x_n+1，y_n+1)，则此时各避障路径的位置坐标方程表示为

适应度函数为

上式中，f_1，j=d_f-r_j，r_j为机器人准确选取避障路径的概率；d_f为第j条路径被机器人选取的概率.

在确定适应度函数的基础上，对机器人避障路径进行排序，其结果如下式所示

上式中，(x_q(t)，y_q(t))为路径q在t时刻的位置，(x_p(t)，y_p(t))为路径p在t时刻的位置.

在排序基础上引入视觉分析法，对已排序的避障路径进行分析，必须先确定避障路径的特征线性频率尺度，从而为识别最优避障路径提供依据.特征线性频率尺度表达式如下所示

其中，N为尺度个数，k为比例因子，${{\overline{A}}_{0}}$为2个避障路径间中心频率的比例因子.

此时机器人避障路径识别结果可表示为

上式中，e_no(x，y)为避障路径(x，y)的置信度，A_no(x，y)为避障路径(x，y)的估计值，T为技术参数，ε为机器人避障路径识别参数.当ε≤0且T＞0时，P(x，y)处于最优避障路径；反之，当ε＞0且T＜0时，P(x，y)为最差的避障路径，可直接忽略.

综上所述，在采用基于RBPF的SLAM方法对机器人避障路径进行滤波预处理以降低外界对避障路径干扰的基础上，依据适应度函数对避障路径进行排序，并引入视觉分析法，即可实现对机器人最优避障路径的有效识别.

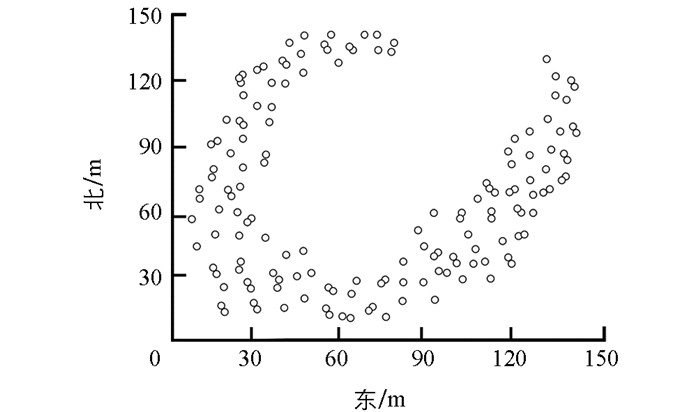
为验证改进的识别方法在真实环境中的有效性与可行性，与传统基于地理门槛的机器人避障路径识别方法及SAO分析方法进行比对，本文设计了如下实验：选用Data set数据集中的数据，利用指定的机器人(如图 1)，在指定大小为150×150 m²的公园(如图 2)中进行验证实验.实验环境中主要障碍物为树木.其中，150×150 m²的仿真实验环境中共含有150个障碍物.仿真环境的障碍物分布情况如图 3所示.

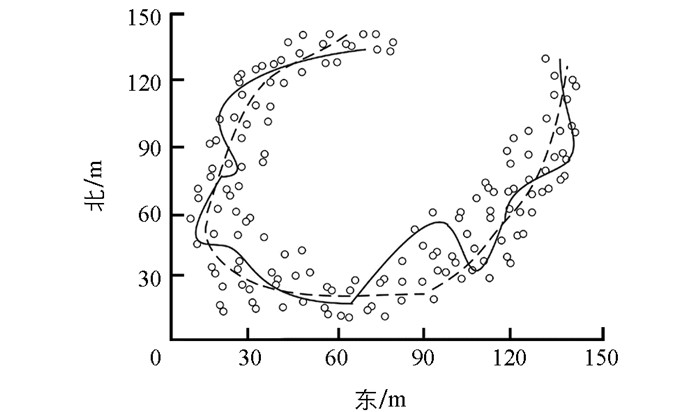
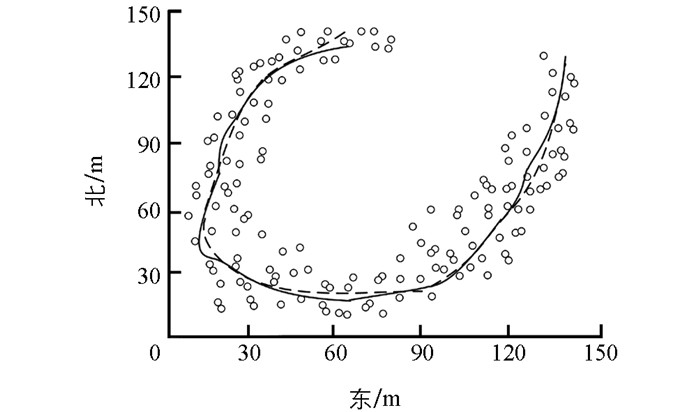
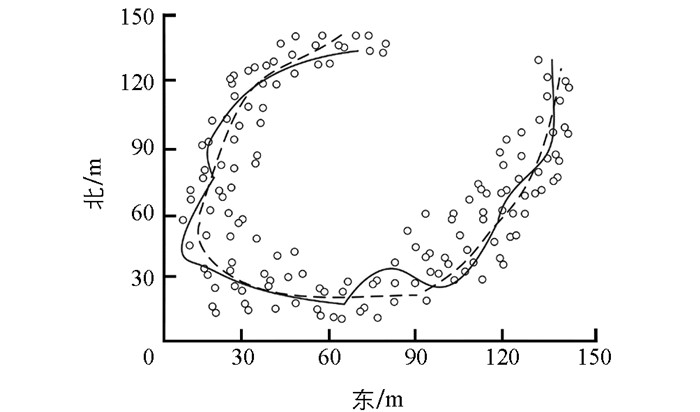
设定速度噪声σ_v=0.1 m/s，角度噪声σ_γ=2°，测试硬件参数为2.26 GHz. Intel Core i5 CPU，4 GB内存.实验对比结果如图 4~6所示.

由图 4~6可知，采用传统的基于地理门槛的避障路径识别方法时，机器人初期便远离实际路径，虽在中途回归实际路径，但随即又出现偏离，实验全程偏离及回归实际路径达到9次.这表明，传统基于地理门槛的识别方法对周围环境及路径识别的准确度偏低.采用SAO分析方法时，全程共出现6次偏离实际路径的情况，偏离幅度较大，且实验大部分时间内机器人所识别路径与实际路径不吻合.这表明，基于SAO分析的识别方法，同样存在对周围环境及路径识别准确度低的问题.采用改进的算法时，全程共出现4次偏离实际路径的情况，均在偏离幅度不大的情况下，并在较短时间内回归实际路径，而且在实验的大部分时间内均与实际路径吻合.由此可证，本文提出的改进方法对避障路径和周围环境的识别精度较高，适合大范围、长时间使用，具有一定的优势.

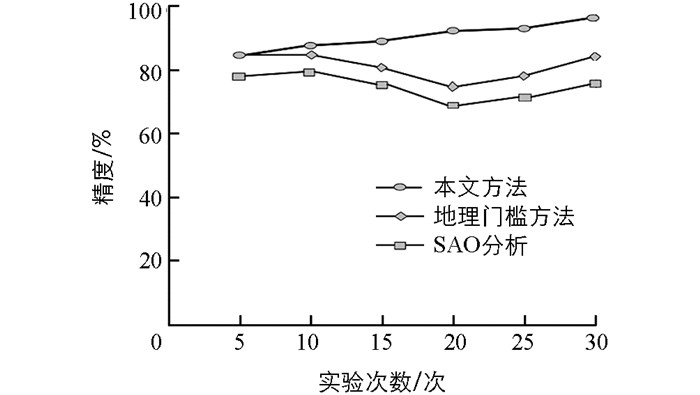
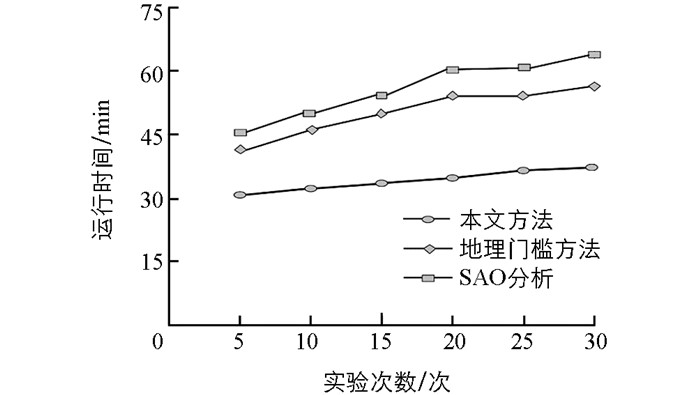
在仿真环境中，将3种方法分别运行30次，以识别精度和运行耗费时间为标准进行比较，结果如图 7~8所示.

由图 7可知，在采用传统基于地理门槛的机器人避障路径识别方法时，识别精度约为84.5%，且在第10~20次实验时出现了精度显著下降的情况，此后虽有所回升，但回升幅度有限.采用基于SAO分析的识别方法时，识别精度约为76.8%，且随实验次数的增加出现大幅度波动.采用本文所提出的改进方法时，其识别精度约为93.4%，相比地理门槛方法、SAO分析法，分别提高了约8.9%，16.6%，且随着实验次数的增加，在相当程度上呈现了学习曲线，具有一定的优势.

由图 8可知，采用传统的基于地理门槛的机器人避障路径识别方法时，运行耗费时间约为51.2 min，且在第10~20次实验时出现耗时大幅度增加的现象.采用基于SAO分析的方法时，运行耗费时间约为58.9 min，且耗时随实验次数大幅度增加.采用本文所提出的改进方法时，运行时间耗费约为35.9 min，耗时随实验次数增加的幅度不大.总体上，改进的方法与地理门槛方法、SAO分析法比较，平均运行时间分别降低了约15.3 min，23 min，说明改进的方法具有一定的鲁棒性.

针对传统识别方法准确度低、效率差的问题，本文提出了一种基于视觉分析的机器人最优避障路径识别方法.通过建立机器人避障路径观测模型，对机器人的运动状态进行分析；采用基于RBPF的SLAM方法对避障路径进行降噪滤波处理；在此基础上依据适应度函数对避障路径进行排序，再引入视觉分析法对排序后的避障路径进行识别，最终实现对最优避障路径的有效识别.实验结果证明，改进的方法与传统的识别方法相比，识别精度较高，运行耗费时间较短，具有一定的实用性.