-
考虑如下的无约束优化问题
其中f(x)是连续可微函数,其梯度向量
$\nabla $ f(x)记为g(x).共轭梯度法是求解上述无约束优化问题的一种十分有效的算法.经典共轭梯度法的基本迭代格式为:其中:dk为搜索方向;αk为步长因子,通常可以由Wolfe非精确的一维线搜索来确定.
δ和σ为满足0<δ<σ<1的常数;βk为标量参数.关于βk的选择有许多著名的公式,如:
其中yk-1=gk-gk-1.上述4个公式分别对应4种不同的共轭梯度方法.每种方法又有很多变形,例如Wei等[1]给出了PRP的一个变形,参数βk取值为:
WYL法继承了PRP法的一些优良性质,例如良好的数值表现,并且Huang等[2]证明了此方法在强Wolfe线搜索下具有全局收敛性和下降性.
2001年Birgin和Martinez[3]提出了一种谱共轭梯度法,其搜索方向定义如下:
其中
${\theta _k} = \frac{{{\boldsymbol{s}_{k-1}}^{\text{T}}{\boldsymbol{s}_{k-1}}}}{{{\boldsymbol{s}_{k-1}}^{\text{T}}{\boldsymbol{y}_{k - 1}}}} $ 为谱系数,$ {\beta _k} = \frac{{{{\left( {{\theta _k}{\boldsymbol{y}_{k-1}}-{\boldsymbol{s}_{k-1}}} \right)}^{\text{T}}}{\boldsymbol{y}_{k - 1}}}}{{{\boldsymbol{d}_{k - 1}}^{\text{T}}{\boldsymbol{y}_{k - 1}}}}$ ,sk-1=xk-xk-1=αk-1dk-1.但是Birgin和Martinez提出的谱共轭梯度法的搜索方向dk不满足下降性,当然也不具有全局收敛性.为了获得全局收敛性,Zhang等[4]在此基础上构造出了FR型谱共轭梯度法,其搜索方向dk中${\theta _k} = \frac{{{\boldsymbol{d}_{k-1}}^{\text{T}}{\boldsymbol{y}_{k-1}}}}{{{{\left\| {{\boldsymbol{g}_{k-1}}} \right\|}^2}}} $ ,βk=βkFR.此方法的一个重要特点是满足充分下降条件其中t>0为常数.此后Wang,Cao等[5-6]提出了CD型谱共轭梯度法;Du和Liu提出了HS型谱共轭梯度法[7];Wan,Huang等[8-9]提出了PRP型的谱共轭梯度法.上述方法都满足充分下降条件(8).
本文在上述文献的基础上,提出了一类具有充分下降性的混合型谱共轭梯度法,参数βk为:
谱系数
${\theta _k} = c + \beta _k^{{\text{WS}}}\frac{{\boldsymbol{g}_k^{\text{T}}{\boldsymbol{d}_{k-1}}}}{{{{\left\| {{\boldsymbol{g}_k}} \right\|}^2}}} $ ,c为大于0的参数,然后基于(9) 式给出混合型谱共轭梯度法的算法,证明了算法的收敛性,并进行了数值实验.
全文HTML
-
本节中,首先给出混合型谱共轭梯度法(算法1),然后说明它所具有的一些性质.
算法1 混合型谱共轭梯度法.
步骤1 给定初始点x1及精度ε,计算g1,若‖g1‖≤ε,停止.否则,转步骤2.
步骤2 计算搜索方向dk
步骤3 由(4) 式计算步长因子αk.
步骤4 迭代计算xk+1=xk+αkdk,gk+1=g(xk+1).若‖gk+1‖≤ε,则停止.
步骤5 k:=k+1,转步骤2.
命题1 由算法1产生的序列{gk}和{dk}满足下降性,即对任意k≥1,都有gkTdk<0.
证 由算法1得
命题2 对任意k≥1,参数βkWS满足
$ 0 \leqslant \beta _k^{{\text{WS}}} \leqslant \frac{{{{\left\| {{\boldsymbol{g}_k}} \right\|}^2}}}{{{{\left\| {{\boldsymbol{g}_{k-1}}} \right\|}^2}}}$ .证 由参数βkWS的定义可知命题成立.
分析(9) 式有:参数βkWS为FR,WYL,PRP 3者的混合.下面分3种情况对此说明:
1) 当gkTgk-1≤0时,
2) 当gkTgk-1>0且
$\frac{{\left\| {{\boldsymbol{g}_k}} \right\|}}{{\left\| {{\boldsymbol{g}_{k-1}}} \right\|}} \leqslant 1$ 时,3) 当gkTgk-1>0且
$\frac{{\left\| {{\boldsymbol{g}_k}} \right\|}}{{\left\| {{\boldsymbol{g}_{k-1}}} \right\|}} > 1 $ 时,此外由算法1的谱系数的选取可知,可通过选取不同的参数c来优化算法1的数值效果.
-
为了研究算法的收敛性,下面给出一些基本假设:
(A1) 设f(x)的水平集
$\mathit{\Omega } = \left\{ {\boldsymbol{x} \in {\mathbb{R}^n}|f\left( \boldsymbol{x} \right) \leqslant f\left( {{\boldsymbol{x}_1}} \right)} \right\} $ 有界,其中x1为初始迭代点.(A2) 存在Ω的某个邻域Λ,使得f(x)在该邻域上连续可微且梯度函数g(x)满足Lipschitz条件,即存在常数L>0,使得
引理1[10] 假设(A1),(A2) 成立,如果搜索方向dk满足下降性,步长αk由Wolfe非精确的一维线搜索确定,那么
$\sum {\frac{{{{\left( {\boldsymbol{g}_k^{\text{T}}{\boldsymbol{d}_k}} \right)}^2}}}{{{{\left\| {{\boldsymbol{d}_k}} \right\|}^2}}}} < \infty $ .定理1 如果条件(A1),(A2) 成立,算法1产生的序列{gk}有
证 假设结论不成立,则存在常数γ>0使得
由(10) 式可得
从而有
将(19) 式展开得
移项可得
由命题1的证明,(21) 式可变为
(22) 式两边同时除以(gkTdk)2得
进而有
综上所述可得
与引理1矛盾.
-
下面对算法1进行数值实验,测试函数中Example 1与Example 2的表达式为:
其它测试对象均来自文献[11]中的函数.实验在PC机上完成,PC的配置如下:AMD A4-3300M CPU 1.90 GHz,2.00 GB内存.程序用Matlab编写,运行环境为Matlab R2010a.算法中参数的选取为:δ=0.001,σ=0.9.终止条件为:‖gk‖≤10-4;或者算法的迭代总时间超过1 800 s;或者超过规定的迭代次数.
对于算法1中参数c的选取,以二维的香蕉函数为实验对象进行测试,香蕉函数的表达式如下:
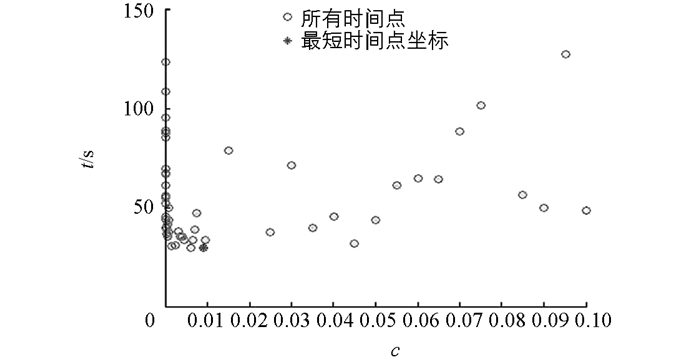
选取不同的c值(0<c<0.1),得到不同的迭代时间t,作出c-t图(图 1).
由图 1可得:当c取0.009时,迭代时间最短,最短时间点坐标为(0.009,29.498 5).另外通过数值实验发现,当c取值大于0且小于106时,算法1仍然有效;但当c取值为0或大于106的时候,算法1无效.所以在本文后面的数值实验中选取c=0.009,将算法1与WYL共轭梯度法及FR共轭梯度法进行比较,实验结果见表 1.
在表 1中i的取值0和1分别表示迭代成功与不成功.从表 1可以看出无论是迭代次数、迭代的总时间、还是每次迭代的平均时间,算法1数值效果均优于其它另外两种算法.此外算法1可以调控参数c来优化数值效果,具有一定的灵活性.



 下载:
下载: