高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

改进DES子密钥使用顺序的算法研究

,  , 

上一篇

下一篇

刘海峰, 朱婧, 曹慧. 改进DES子密钥使用顺序的算法研究[J]. 西南大学学报（自然科学版）, 2017, 39(6): 135-140. doi: 10.13718/j.cnki.xdzk.2017.06.021
引用本文: 刘海峰, 朱婧, 曹慧. 改进DES子密钥使用顺序的算法研究[J]. 西南大学学报（自然科学版）, 2017, 39(6): 135-140. doi: 10.13718/j.cnki.xdzk.2017.06.021
shu
Hai-feng LIU, Jing ZHU, Hui CAO. Research of Improving the Algorithm of DES Subkey Usage Order[J]. Journal of Southwest University Natural Science Edition, 2017, 39(6): 135-140. doi: 10.13718/j.cnki.xdzk.2017.06.021
Citation: Hai-feng LIU, Jing ZHU, Hui CAO. Research of Improving the Algorithm of DES Subkey Usage Order[J]. Journal of Southwest University Natural Science Edition, 2017, 39(6): 135-140. doi: 10.13718/j.cnki.xdzk.2017.06.021
shu

改进DES子密钥使用顺序的算法研究

  • 1.

    陕西科技大学 文理学院，西安 710021

  • 2.

    陕西科技大学 电气与信息工程学院，西安 710021

  • 基金项目: 国家自然科学基金 (11301314)；陕西省自然科学基金 (2014JQ1025)
详细信息
    作者简介:

    刘海峰 (1964-)，男，陕西泾阳人，副教授，硕士，主要从事计算机网络与信息安全及代数编码与密码学的研究 .

  • 中图分类号: TN918.4

Research of Improving the Algorithm of DES Subkey Usage Order

  • 1.

    School of Arts & Sciences, Shaanxi University of Science & Technology, Xi'an 710021, China

  • 2.

    School of Electrical & Information Engineering, Shaanxi University of Science & Technology, Xi'an 710021, China

  • 摘要: 通过对DES算法进行分析，针对DES易受穷举搜索等方法攻击的缺陷，提出基于分组与哈希函数的改进方案.该改进方案首先将明文与密钥进行异或，然后根据分组结果或者哈希表查找比较次数，结合仿射变换决定子密钥的使用顺序，最后利用RSA加密子密钥的使用顺序.该改进方案因为输入明文的不同而引起子密钥的使用顺序不同，使得每次破解都需要16!次穷举，从而提高穷举搜索与选择明文攻击的难度，提高DES算法的安全性.
    Abstract: The data encryption standard (DES) is liable to suffer from exhaustive attack. Through DES algorithm analysis, this paper puts forward two improved schemes based on grouping and Hash function to solve the defect. First, exclusive OR (XOR) is performed on the plaintext and the key. Then, according to the grouping result or the comparison times in Hash table lookup, and combined with affine transformation, the improved algorithms determine the subkey order. Finally, RSA is used to encrypt the subkey order. With the proposed algorithms, different input plaintexts cause different subkey orders, so every crack needs 16! exhaustive searches. Consequently, the ability to resist exhaustive attack and chosen plaintext attack is improved and the security of DES algorithm is enhanced.
  • 加载中

  • 图 1  DES加密处理图

    下载: 全尺寸图片 幻灯片

    图 2  S盒代替

    下载: 全尺寸图片 幻灯片

    表 1  扩展变换E的变换表

    32 01 02 03 04 05
    04 05 06 07 08 09
    08 09 10 11 12 13
    12 13 14 15 16 17
    16 17 18 19 20 21
    20 21 22 23 24 25
    24 25 26 27 28 29
    28 29 30 31 32 01
    下载: 导出CSV

    表 2  置换运算P

    16 7 20 21 29 12 28 17
    1 15 23 26 5 18 31 10
    2 8 24 14 32 27 3 9
    19 13 30 6 22 11 4 25
    下载: 导出CSV

    表 3  置换选择1

    57 49 41 33 25 17 9 1 58 50 42 34 26 18
    10 2 59 51 43 35 27 19 11 3 60 52 44 36
    63 55 47 39 31 33 15 7 62 54 46 38 30 22
    14 6 61 53 45 37 29 21 13 5 28 20 12 4
    下载: 导出CSV

    表 4  循环左移

    轮序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
    移位数 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1
    下载: 导出CSV

    表 5  置换选择2

    14 17 11 24 1 5
    3 28 15 6 21 10
    23 19 12 4 26 8
    16 7 27 20 13 2
    41 52 31 37 47 55
    30 40 51 45 33 48
    44 49 39 56 34 53
    46 42 50 36 29 32
    下载: 导出CSV

    表 6  哈希表

    地址 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
    待散列元素 1 2 1 1 2 1 7 1 2 1 7 1 2 14 1 14
    比较次数 1 1 3 4 4 6 1 8 8 10 5 12 12 1 15 3
    下载: 导出CSV
  • [1] 胡向东, 魏琴芳.应用密码学[M].北京:电子工业出版社, 2006.
    [2] 盛利元, 张卿, 孙克辉, 等.一种基于混沌映射的DES密钥空间拓展方法[J].通信学报, 2005, 26(4): 122-124, 141. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-TXXB200504020.htm
    [3] 李海峰, 马海云, 徐燕文.现代密码学原理及应用[M].北京:国防工业出版社, 2013: 97-100.
    [4] 谢志强, 高鹏飞, 杨静.基于前缀码的DES算法改进研究[J].计算机工程与应用, 2009, 45(9): 92-94, 119. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200909027.htm
    [5] 潘立登, 盛乃军.网络通信中的基本安全技术[J].电子技术应用, 2000, 26(3): 4-7. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-LYLA200002006.htm
    [6] 邱伟星, 李钦, 许金莲, 等.一种DES组合算法[J].南京邮电大学学报 (自然科学版), 2011, 31(5): 83-86, 96. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-NJYD201105018.htm
    [7] SCHNEIER B. 应用密码学: 协议、算法与C源程序[M]. 吴世忠, 祝世雄, 张文政, 译. 2版. 北京: 机械工业出版社, 2014: 191-196.
    [8] 段博佳, 袁家斌, 杨婕, 等.分组加密算法的并行量子搜索攻击的研究[J].小型微型计算机系统, 2011, 32(9): 1908-1912. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-XXWX201109041.htm
    [9] KATZ J, LINDEU Y. 现代密码学: 原理与协议[M]. 任伟, 译. 北京: 国防工业出版社, 2011: 110-116.
    [10] TRAPPE W, WASHINGTON L C. 密码学与编码理论[M]. 王全龙, 王鹏, 林昌露, 译. 2版. 北京: 人民邮电出版社, 2008.
    [11] 张福泰, 李继国, 王晓明, 等.密码学教程:信息安全系列教材[M].武汉:武汉大学出版社, 2006.
  • 加载中
图( 2) 表( 6)
计量
  • 文章访问数:  968
  • HTML全文浏览数:  525
  • PDF下载数:  209
  • 施引文献:  0
出版历程
  • 收稿日期:  2017-03-02
  • 刊出日期:  2017-06-20

改进DES子密钥使用顺序的算法研究

    作者简介: 刘海峰 (1964-)，男，陕西泾阳人，副教授，硕士，主要从事计算机网络与信息安全及代数编码与密码学的研究
  • 1. 陕西科技大学 文理学院，西安 710021
  • 2. 陕西科技大学 电气与信息工程学院，西安 710021
  • 收稿日期:  2017-03-02
基金项目:  国家自然科学基金 (11301314)；陕西省自然科学基金 (2014JQ1025)

摘要: 通过对DES算法进行分析，针对DES易受穷举搜索等方法攻击的缺陷，提出基于分组与哈希函数的改进方案.该改进方案首先将明文与密钥进行异或，然后根据分组结果或者哈希表查找比较次数，结合仿射变换决定子密钥的使用顺序，最后利用RSA加密子密钥的使用顺序.该改进方案因为输入明文的不同而引起子密钥的使用顺序不同，使得每次破解都需要16!次穷举，从而提高穷举搜索与选择明文攻击的难度，提高DES算法的安全性.

English Abstract

    全文HTML

  • 20世纪70年代初，IBM在美国国家安全局 (NSA) 和美国国家标准局 (NBS) 的帮助与监督下开发出了数据加密标准 (Data Encryption Standard，DES)，并被美国国家标准局确定为联邦信息处理标准 (FIPS PUB 46)，得到广泛应用. DES作为美国加密标准已经到期，但在我国DES在POS、ATM、智能卡 (IC卡)、加油站、高速公路收费站等领域现被广泛应用，以此来实现关键数据的保密[1].

    Biham和Shamir在80年代末提出差分密码分析，对DES的攻击虽比蛮力搜索用时更少，但攻击者很难获得足够的明文进行选择明文攻击，只是理论上的突破，并没有太大的实际意义；Matsui在90年代早期提出线性密码分析，它不再需要选择明文攻击，但仍然很难获得足够的输入/输出对.对DES最实用的攻击是穷举搜索，主要是因为DES的密钥长度较短，使得穷举搜索成为可能.若能将DES的密钥空间拓展到穷举法也无法破译，则理论上DES加密算法仍然是安全的[2].二重DES将密钥长度增加到112位，但容易遭受中间相遇攻击，使有效密钥长度降为56位，破译二重DES的难度为257量级[3].针对DES易受穷举搜索攻击及二重DES易受中间相遇攻击的问题，本文提出新的思路来改进DES的算法，提高DES的安全性.

1.   DES简介

  • DES是一种分组密码，它以64位为分组长度[4]. 64位为一组的明文，经过长度为64位的密钥进行加密 (实际长度为56位，其中第8，16，24，32，40，48，56，64位为奇偶校验位，可以忽略)，得到64位为一组的密文. DES是一种对称密钥加密体制 (私钥加密体制)，它使用同一组密钥对消息进行加密和解密[5]；DES同时是一种对称算法，解密过程与加密过程相似，解密过程可以使用加密过程的算法，只不过密钥的使用顺序正好相反，即当加密过程使用的密钥顺序为K0K1K2…K14K15，解密过程的密钥使用顺序为K15K14…K2K1K0. DES公开了它的加密流程和具体实现步骤，从它的整个体制可以看出，DES分为2个部分：DES加密部分和子密钥生成部分[6]，密钥部分独立运行，产生加密过程所需的子密钥然后作用于DES.

    • 1.1.   DES算法加密过程

  • DES算法的加密过程经历了3个阶段，如图 1所示[1].

    • 1.1.1.   初始置换IP与逆初始置换IP-1

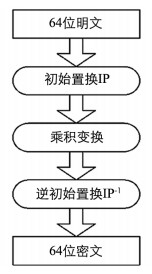
  • 根据DES公布的初始置换表与逆初始置换表可以看出，这2个过程的置换是互逆的.例如，初始置换IP把信息的第2位置换到第8位的位置，逆初始置换IP-1把经过加密的信息的第8位又置换到第2位，并形成最终的密文.初始置换IP与对应的逆初始置换IP-1并不影响DES的安全性. DES这种置换结构的主要目的是为了更容易地将明文和密文数据以字节大小放入DES芯片中，但这种方式的置换软件实现很困难，对算法的安全性又没有影响，所以DES的许多软件实现方式删去了初始置换IP和逆初始置换IP-1[7].

    • 1.1.2.   乘积变换

  • 乘积变换中包括16轮的迭代，每轮变换的逻辑关系为

    F变换包括3部分：扩展变换E、选择压缩变换S盒代替、置换运算P[8].扩展变换E的目的是将32位右半部分数据变为48位，从而能够与48位密钥异或，并且提供了更长的结果使得S盒能够压缩.但它的主要目的是使输出对输入的依赖性传播得更快，产生雪崩效应[7].其扩展变换E的变换表如表 1所示.

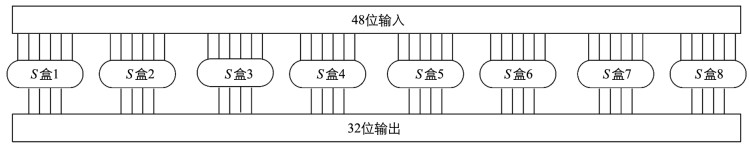
    选择压缩变换S盒代替是整个DES中唯一的一个非线性部分，专门用来对抗差分密码分析 (某种程度上) 的[9].将48位的输入分成8组，每组6位，6位的数据进入对应S盒后变为4位，共8个S盒，所以48位输入经过S盒代替后产生32位的输出，其代替过程如图 2所示.

    置换运算P将S盒代替运算后的32位输出按照固定的置换P表进行置换，打乱原有次序进行重排，任一位不能映射2次，也不能被略去.置换运算P的定义如表 2所示.

    多重S变换与P变换组成S-P网络. S变换的目的是起到混淆作用，使密文与明文的统计关系尽可能的复杂，实现小块的非线性变换；P变换的目的是起到扩散作用，使明文的每一位尽可能影响密文的多位，从而达到“雪崩效应”，实现大块的非线性变换. S-P网络实现了很好的非线性化和雪崩效应.

    • 1.2.   子密钥生成部分

  • 输入的64位密钥剔除8个奇偶校验位，剩下的56位，经过置换选择1后被分成C0和D0两部分，各28位，C0为置换选择1的前两行，D0为置换选择1的后两行.原密钥的第1位经过置换选择1后变为C0的第8位.原密钥有意义的最后一位第63位经过置换选择1后变为D0的第1位.置换选择1如表 3所示.

    C0，D0分别按表 4进行第一轮的循环左移，得到C1，D1，将得到的C1，D1按表 5进行置换选择2变换得到48位的密钥K0，同时将C1，D1按表 4进行第二轮的循环左移，得到C2，D2，将得到的C2，D2按表 5进行置换选择2变换得到48位的密钥K1，按照此方法，直至得到加密所需的16个子密钥K0K1K2…K14K15. DES中Ci，Di循环左移的总位数分别为28位，所以经过1轮DES加密后密钥正好经过一个轮回.

2.   DES算法安全性分析

  • DES的加密流程和具体实现步骤公开，只要密钥不变，不管加密的明文是什么，它的加密过程都完全相同，这样攻击者就可以通过穷举搜索、选择明文等方法对DES进行攻击. DES的不安全性与它的内部结构和设计是无关的[9]，造成DES的不安全性的一个重要原因是DES的密钥长度太短了，只有64位 (实际上为56位)，密钥空间大小为256.随着计算机运算能力的提高，采用暴力攻击的方法对DES进行破译已经不是难事.通常改进的方法有：多重DES、使用独立子密钥的DES、一次一密等.一次一密被认为是一种不可攻破的密码系统[10]，如果已知一段明文，可以找出相对应的密钥，但这一段密钥对以后密文的破解没有任何用处，因为密钥序列中任意两项是相互独立的[11].一次一密的加密效果虽然很好，但存在密钥太长，生成的代价太大的问题.

    针对一次一密存在的问题，提出通过明文与密钥共同决定DES子密钥的使用顺序，使得即使密钥相同，不同明文加密，DES子密钥的使用顺序不同，以此来提高DES抗攻击的能力.

3.   改进方案及示例

    3.1.   子密钥加密顺序改进方案1及示例

    3.1.1.   改进方案1的步骤

  • 1) 输入64位明文M，并将64位明文与64位密钥K进行异或，得到64位数据C.

    2) 将得到的64位二进制数据C，每4位进行分组，得到16个大小在0~15之间的数据Ci(i为0~15).

    3) 令原子密钥的顺序为：K0K1K2…K14K15，采用下面的算法对子密钥的顺序进行交换，若Ci(i为0~15) 的值为j，选定参数B，计算B*i+j的值 (当B=1时，由仿射变换退化到移位操作)，为了避免B*i+j的值大于15，再采用模16求余以确保B*i+j的值在0~15之间，将Ki的值与K(B*i+j)%16进行交换.

    4) 按照改进后的子密钥顺序进行DES加密.

    5) 由于解密的需要，将变换后的子密钥顺序的下标序列作为明文进行加密 (可以利用接收方的公钥进行RSA加密)，并与密文一起传送给接收方.

    6) 解密时接收方利用RSA私钥对子密钥顺序的下标序列密文进行解密，得到变换后的子密钥顺序的下标序列的明文，执行DES的逆过程即可得到明文.

    • 3.1.2.   示例说明子密钥变换过程

  • 1) 选取明文M=00000001 00100011 01000101 01100111 10001001 10101011 11001101 11101111.选取密钥K=00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001.将明文M与密钥K进行异或得到数据C=00010010 00010111 00010010 00011110 00010010 00010111 00010010 00011110.

    2) 将二进制数据C每4位进行分组，得到16个十进制数值为{1，2，1，7，1，2，1，14，1，2，1，7，1，2，1，14}.

    3) 令B=1.根据上面序列，C0=1所以K0与K1交换，经过一次交换子密钥的顺序为：K1K0K2K3K4K5K6K7K8K9K10K11K12K13K14K15；同理C1=2所以K1与K3交换，经过二次交换子密钥的顺序为：K3K0K2K1K4K5K6K7K8K9K10K11K12K13K14K15；以此类推，经过16次交换后，子密钥的顺序为：K11K0K2K1K6K4K5K7K10K8K3K9K14K12K13K15.

    4) 按此改进后的子密钥的顺序K11K0K2K1K6K4K5K7K10K8K3K9K14K12K13K15进行DES加密.

    5) 改进后的子密钥顺序的下标序列为11，0，2，1，6，4，5，7，10，8，3，9，14，12，13，15，对这个序列利用接收方的公钥 (假设公钥PK={3，33}) 进行RSA加密，得到的密文为11，0，8，1，18，31，26，13，10，17，27，3，5，12，19，9，以便解密时使用.

    6) 解密时接收方利用RSA私钥 (相对应的私钥SK={7，33}) 对子密钥顺序的下标序列密文进行解密，得到变换后的子密钥顺序的下标序列的明文为11，0，2，1，6，4，5，7，10，8，3，9，14，12，13，15，即子密钥的顺序为K11K0K2K1K6K4K5K7K10K8K3K9K14K12K13K15，执行DES的逆过程即可得到明文.

    • 3.2.   子密钥加密顺序改进方案2及示例

    3.2.1.   改进方案2的步骤

  • 1) 输入64位明文M，并将64位明文与64位密钥K进行异或，得到64位数据C.

    2) 将得到的64位二进制数据C，每4位进行分组，得到16个大小在0~15之间的数据Ci(i为0~15).

    3) 利用哈希函数和线性探测处理冲突的方法将数据Ci放入哈希表中，根据按顺序放数据C0C1C2…C14C15时所进行的地址计算次数 (或者说是查找数据C0C1C2…C14C15时所进行的关键数比较次数)，得到16个十进制数据{A0，A1，A2，…，A14，A15}.

    4) 令原子密钥的顺序为：K0K1K2…K14K15，采用下面的算法对子密钥的顺序进行交换，若Ai(i为0~15) 的值为j，选定参数B，计算B*i+j的值 (当B=1时，由仿射变换退化到移位操作)，为了避免B*i+j的值大于15，再采用模16求余以确保B*i+j的值在0~15之间，将Ki的值与K(B*i+j)%16进行交换.

    5) 按照改进后的子密钥顺序进行DES加密.

    6) 由于解密的需要，将变换后的子密钥顺序的下标序列作为明文进行加密 (可以利用接收方的公钥进行RSA加密)，并与密文一起传送给接收方.

    7) 解密时接收方利用RSA私钥对子密钥顺序的下标序列密文进行解密，得到变换后的子密钥顺序的下标序列的明文，执行DES的逆过程即可得到明文.

    • 3.2.2.   示例说明子密钥变换过程

  • 1) 选取明文M=00000001 00100011 01000101 01100111 10001001 10101011 11001101 11101111.选取密钥K=00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001.将明文M与密钥K进行异或得到数据C=00010010 00010111 00010010 00011110 00010010 00010111 00010010 00011110.

    2) 将二进制数据C每4位进行分组，得到16个十进制数值G={1，2，1，7，1，2，1，14，1，2，1，7，1，2，1，14}.

    3) 采用除留余数法构造哈希函数，待散列数据的长度为16，令哈希表长度m，p均为17，则哈希函数为：H(Gi)=Gi%17(i=0，1，2，…，15)，当发生冲突时采用线性探测再散列法处理冲突，得到如表 6所示的哈希表.按顺序查找16个十进制数值所进行的比较次数为A={1，1，3，1，4，4，6，1，8，8，10，5，12，12，15，3}.其中，地址比较次数的范围为1~16.

    4) 令B=1.根据上面序列，A0=1所以K0与K1交换，经过一次交换子密钥的顺序为：K1K0K2K3K4K5K6K7K8K9K10K11K12K13K14K15；同理A1=1所以K1与K2交换，经过二次交换子密钥的顺序为：K2K0K1K3K4K5K6K7K8K9K10K11K12K13K14K15；以此类推，经过16次交换后，子密钥的顺序为：K1K12K14K7K3K15K8K11K10K5K4K0K6K9K13K2.

    5) 按此改进后的子密钥的顺序K1K12K14K7K3K15K8K11K10K5K4K0K6K9K13K2进行DES加密.

    6) 改进后的子密钥顺序的下标序列为1，12，14，7，3，15，8，11，10，5，4，0，6，9，13，2，对这个序列利用接收方的公钥 (假设公钥PK={3，33}) 进行RSA加密，得到的密文为1，12，5，13，27，9，17，11，10，26，31，0，18，3，19，8，以便解密时使用.

    7) 解密时接收方利用RSA私钥 (相对应的私钥SK={7，33}) 对子密钥顺序的下标序列密文进行解密，得到变换后的子密钥顺序的下标序列的明文为1，12，14，7，3，15，8，11，10，5，4，0，6，9，13，2，即子密钥的顺序为K1K12K14K7K3K15K8K11K10K5K4K0K6K9K13K2，执行DES的逆过程即可得到明文.

4.   算法分析

  • 求证：这种改进DES方式是有效的.

    证明：DES分为2个部分，DES加密部分和子密钥生成部分，子密钥生成部分与DES加密部分相互独立，由密钥生成16个子密钥，并参与到DES加密过程中.这种改进都只是改变子密钥的使用顺序，而不影响DES加密过程，保留了DES的内部结构和设计. DES的加密效果只取决于DES变换本身，与输入无关，因此使用该方法进行改进后的DES仍然具有原DES所具有的雪崩效应和变化均匀性，这种改进DES方式是有效的.

    求证：这种改进DES方式攻击的难度上升.

    证明：改进DES加密使用的子密钥的顺序不仅与密钥有关还与明文有关，随着输入明文的不同即使密钥没变，子密钥的使用顺序也发生改变.攻击者在攻击时，不仅需要知道密钥，还需要知道密钥的使用顺序，而密钥的使用顺序有2个获取途径：① 对发送方经过RSA加密后的子密钥使用顺序进行解密；② 密钥与明文进行异或，按照发送方子密钥使用顺序的产生过程，攻击者自己产生发送方的子密钥使用顺序.对于第一种方法，攻击者需要知道接收方的私钥，而RSA的安全性是基于大数因子分解，由于大数因子分解在数学上没有行之有效的算法，因此该加密技术的破译是相当困难的[5].对于第二种方法也很难实现，攻击者无法知道明文，并且攻击者同样无法知道密钥的使用顺序是如何产生的.所以从理论上这种改进DES方法攻击的难度上升.并且每次随着输入明文的不同子密钥的使用顺序发生变化，每次都要进行16!次穷举，所以对于攻击者来说这种改进DES方法从操作上难度上升了，对它进行攻击的代价也随之上升.

5.   总结

  • DES具有很好的内部结构与设计，它的不安全性主要是易受穷举搜索攻击.本文提出了2种改变子密钥使用顺序的方法，随着输入明文的不同即使密钥相同，子密钥使用顺序也不同，使得每次破解都需要16!次穷举，从而在DES原有破解难度的基础上，提高了穷举搜索攻击与选择明文攻击的难度，提高了DES的安全性.改进的DES方式采用RSA加密子密钥的使用顺序，进一步提高了DES的安全性，使其能够更有效地保护数据.

参考文献 (11)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回