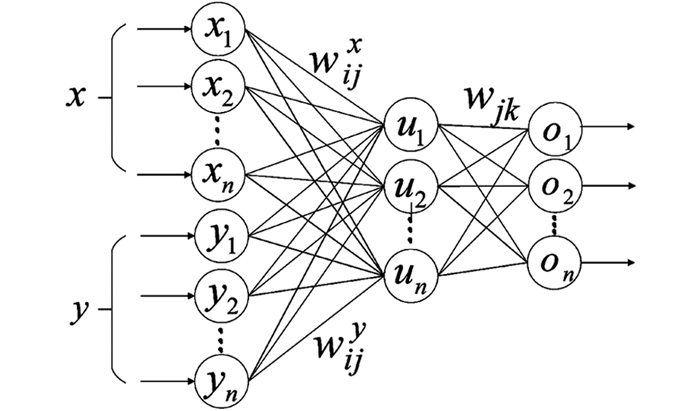
典型的人工神经网络由输入层、隐含层和输出层组成，考虑一个三层人工神经网络如图 1.现假定其中x=[x₁，x₂，…，x_n]，y=[y₁，y₂，…，y_n]都是输入层变量，u=[u₁，u₂，…，u_n]是隐含层的输出量，o=[o₁，o₂，…，o_n]是输出层信号. w^x_xiuj=(w_ij)^x，i=1，2，…，n，j=1，2，…，n是连接第i个输入x_i到第j个隐含层神经元u_j的突触权值，w^y_yiuj=(w_ij)^y，i=1，2，…，n，j=1，2，…，n是连接第i个输入信号y_i到第j个隐含层神经元u_j的突触权值，这样就可以得到第j个隐含层神经元的输出公式

式中w_j^x=[w_1j^x，w_2j^x，K w_nj^x]，w_j^y=[w_1j^y，w_2j^y，K w_nj^y]，且函数f是隐含层神经元的激活函数.同理，假定w_uo=(w_jk)^z为连接第j个隐含层神经元到第k个输出层神经元的突触权值，那么可以得到输出层神经元的输出表达式如下

其中，w_k^z=[w_1k，w_2k，…，w_nk]，且函数g为输出层神经元的激活函数.

将上述人工神经网络同模糊逻辑联系起来，考虑一个多输入单输出的模糊推理系统，输入和输出关系被看作是一组X→Y的数学映射，其中X⊂Rⁿ，Y⊂R，假定推理系统的输出是通过N个模糊关系的汇集而得到的，这种模糊关系的形式是

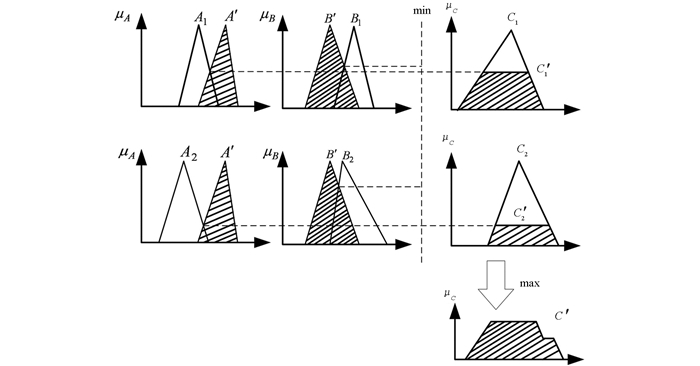
其中x_i，i=1，2，…，n和y分别是输入和输出变量，μ_Ai^m(x_i)，i=1，2，…，n，m=1，2，…，N是{A₁^m，A₂^m，…，A_n^m}模糊集的隶属函数，B^m是定义在输出变量通用集上的模糊集.这里以二输入二规则为例：if A₁ and B₁ then C₁，if A₂ and B₂ then C₂，if A′ and B′ then C′=?，其中A，B，C分别是不同论域X，Y，Z上的模糊集合，推理过程可以用图 2表示.这里采用玛达尼推理削顶法，其几何意义是分别求出A′对A、B′对B的隶属度，并且取这两个之中较小的一个作为总的模糊推理前件的隶属度，再以此为基准去切割后件的隶属度函数，就可以得到结论C′.模糊关系可以表示为[μ_Ai(x)∧μ_Bi(y)]∧μ_Ci(z)，因此可以得到推理结果为

其中“∘”用于表示模糊关系合成，定义如下：如果R和S分别为笛卡尔空间U×V，V×W上的模糊关系，那么R和S的合成可记为R∘S^[6].其计算方法为

其中上确界算子sup表示为

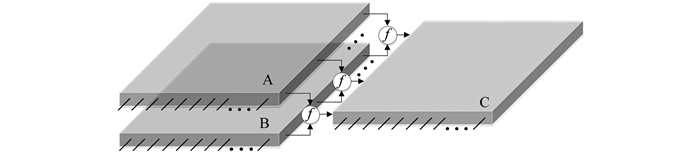
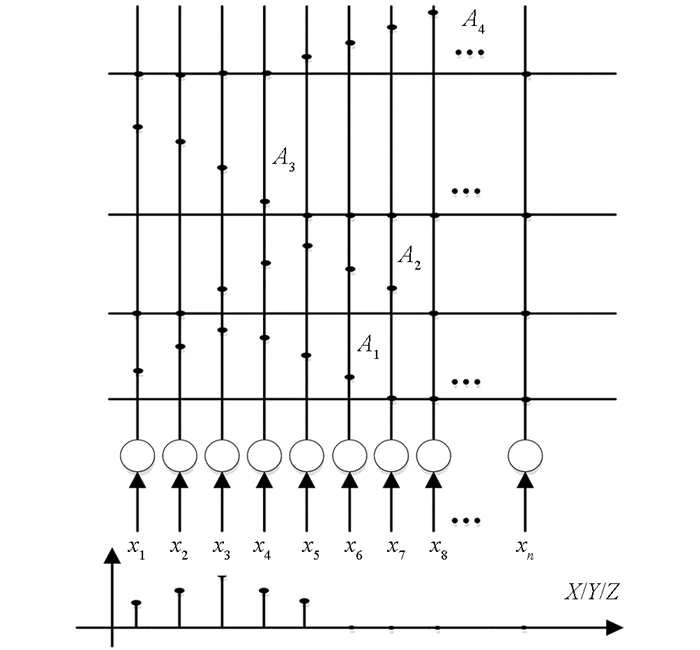
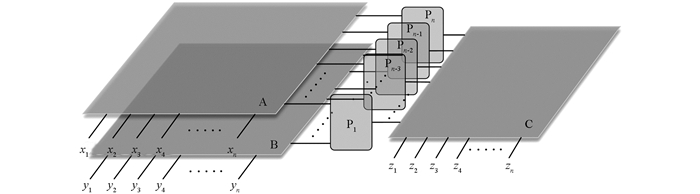
现在构造交叉阵列模糊神经推理系统，考虑二输入单输出模糊推理系统，结构如图 3，其中A，B，C模块均为i行j列的交叉阵列结构，f为激活函数用于实现模糊推理系统的“and”功能. A和B为输入层交叉阵列，C为隐含层交叉阵列，交叉阵列内部结构如图 4所示.图中构造变量X，Y，Z的离散通用集，将模糊输入概念如“x is A”的隶属函数的各个点上的值分配到x₁，x₂，…，x_n中.与此类似，将隶属函数的隶属值存储在各行输入层和隐含层间交叉阵列中，当成与之对应的突触权值，这样就可以将输入层到隐含层的突触权值矩阵存储在交叉阵列中，并且该交叉阵列具有如下特性：能够将产生的输入变量和与之对应的交叉点所存储的权值相乘并实现“and”功能.也就是使进入第j个隐含层神经元的信号等于min(w_ij^xx^T，w_ij^yy^T).隐含层到输出层的权值矩阵也可以用此方法存储在Z模块交叉阵列结构中.

两个相同长度的向量的点积可以表示这两个矢量的相似度：已知幅值小于等于1的矢量A，如图 5所示，给定另外一组向量A₁和A₂，A₁与A相同，A₂为与A相异的向量，那么A·A₁＞A·A₂，且可以推出两向量的点积越大相似度越高.该模糊系统实现推理过程的步骤如下：首先根据公式(1)，选择恰当的激活函数f，即当且仅当输入信号x和y都分别相似于x^x_xiuj和w^y_xiuj时，第二步让第j个隐含层的神经元激活，从而使与激活层相对应的输出层激活强度最大，以达到使输出为取max(min(w_ij^xx^T，w_ij^yy^T))的功能.由此可以看出函数f(·)的功能同“与”门的功能相似.由权值矩阵w_uo决定输出的激活强度，输出层神经元产生的将是输出模糊数的隶属函数，然后经过解模糊就可以得到输出结果.

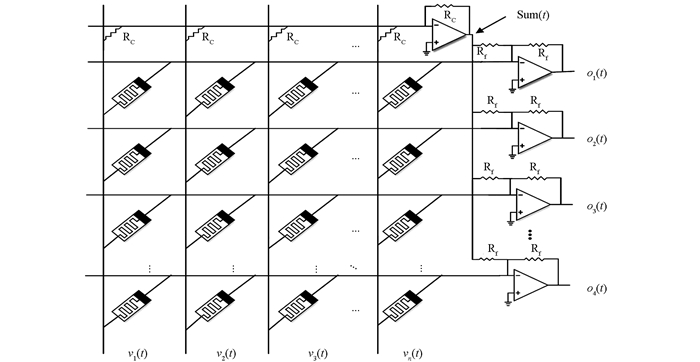
常见的忆阻器交叉阵列结构如图 6所示，这个结构由两组平行的导线相互垂直组成，在每一个交叉点上有一个半导体设备连接两根交叉线，在图中的这种半导体器件是忆阻器^[10-11]，它是一种非线性元器件，忆阻值能够通过改变施加在其两端的电压，使忆阻值在R_on和R_off之间变化. HP忆阻器就是由两层二氧化钛薄膜夹在两个铂(Pt)电极之间组成的，当有电源作用在忆阻器两端时，其两层间的分界面就会移动，阻值就会随着发生变化.

图 6中每一行连接着一个运算放大器的负端，并给这个运算放大器添加一个固定的电阻R_f作为反馈电阻.在顶端一行用固定电阻R_c代替忆阻器，该行组成了一个简单的反向求和电路，因此在任意时刻该求和电路的输出Sum(t)的表达式为

其中v_i(t)是用电压表示的连接第i条垂直线的输入信号，用标准运算放大电路分析方法，可以得出连接第j行的运算放大器的输出表达式为

其中M_ij(t)是当前时刻坐标(i，j)的忆阻值，在公式里，忆阻器被当作是一个简单的电阻，这是因为在计算输出电压时忆阻值是一个恒定值，可以通过对忆阻器施加极短时间的脉冲电压来实现忆阻值的改变，例如采用具有固定的脉冲宽度的矩形脉冲.这种交叉结构需满足的另一前提条件是忆阻器的初始值为R_off，通过提前施加一定时间的电压让忆阻值达到R_off来实现.因此再对不同坐标下忆阻器施加电压，忆阻值就从初始值开始降低，也就是当前储存在坐标(i，j)的值ΔM_ij(t)的表达式为^[8]

将(9)式和(7)式代入(8)式得

当限制忆阻值在很小的范围内变化时，也就是当ΔM_ij(t)/R_off的值远小于1时，简化公式(9)得

其中，

且

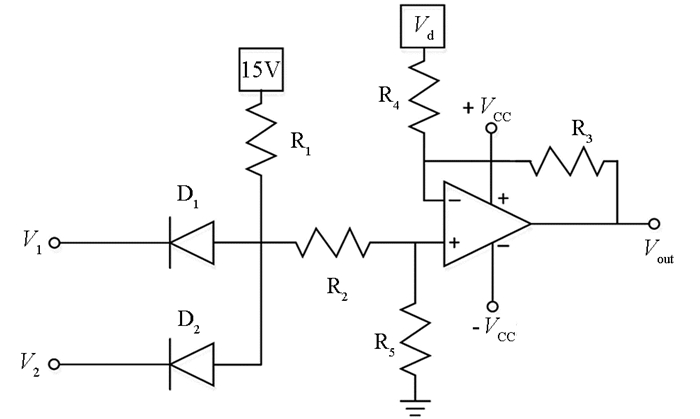
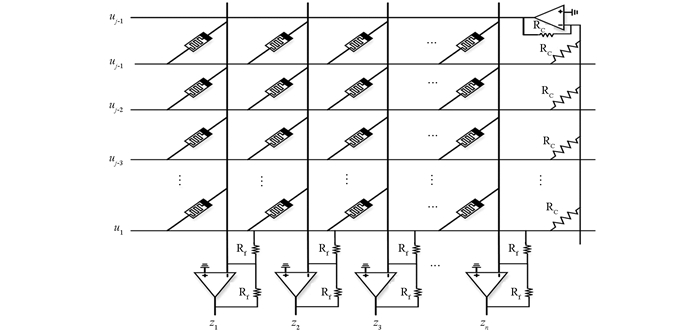
基于图 6的忆阻交叉阵列来实现如图 3所示人工神经网络推理系统，构造结构如图 7所示的模糊推理系统，图 7中模块A，B由图 6所示的交叉阵列结构组成，其中输入x^*=(x₁，x₂，…，x_n)和y^*=(y₁，y₂，…，y_n)分别是输入变量x和y在相同隶属函数下的隶属度，定义x_i=u_A(x_i)，y_i=u_B(y_i)，在输入时将其转换为电压信号，这就构成了图 1所示人工神经网络的输入层，如果系统为多个输入，只需要在模块A和B上方并行增加该种结构即可，模块P₁，P₂，…，P_n-3，P_n-2，P_n-1，P_n用于实现模糊与功能，根据模糊“与”功能须满足当输入为a，b时，T(a)＜T(b).设计模糊“与”功能模块如图 8，图中V₁、V₂是模糊输入数据，D₁和D₂为相同的二级管，R₁、R₂、R₃、R₄、R₅均为10 Ω的电阻，V_d为二极管的导通电压，当输入信号V₁=2sin(20πt)，V₂=2sin(10πt)时仿真结果如图 9所示.模块C的内部结构如图 10，图中R_C是固定电阻，R_f为反馈电阻，R_f的阻值通常由R_off/R_on的比值和所需连接权值的大小决定.这样模块A，B，C就构成了一个由忆阻器交叉阵列组成的模糊神经推理系统.

假设已知许多模糊输入、输出训练数据，在前面所设计的模糊推理系统中构建模糊关系.假定输入集合A，B和输出集合C分别具有隶属函数u_A(x)，u_B(y)和u_C(z)，基于“if A is x^* and B is y^*，then C is z^*”推理规则构建模糊关系，我们将各输入模糊集的隶属度当成电压值，并施加到对应的行和列然后等待t₀秒.例如，如果模糊集A、B、C定义为

将隶属度u_A(x_i)作为电压信号，连接至A模块的最下面一行所对应的列，u_B(y_i)作为电压信号，连接至B模块的最下面一行所对应的列，然后将该行右端接地，其它行接高阻态(即没有电流通过)，电流就会经过最下面一行并引起忆阻值发生变化，这里需要注意的是所有忆阻器的初始值为R_off，那么通过忆阻器的电流值将同施加的电压幅值成正比，于是只需要将所需的隶属函数所对应的隶属度作为电压信号施加到所对应的行，并将该行接地，然后等待较短时间t₀，那么一条模糊规则就会自动存储到模块A和B的交叉阵列中了.模糊规则在交叉阵列的储存形式是以忆阻器的阻值形式存在的，采用经典的HP模型，经过时间t₀，忆阻器的忆阻值表达式为^[13-14]

其中β是一个常数，定义为

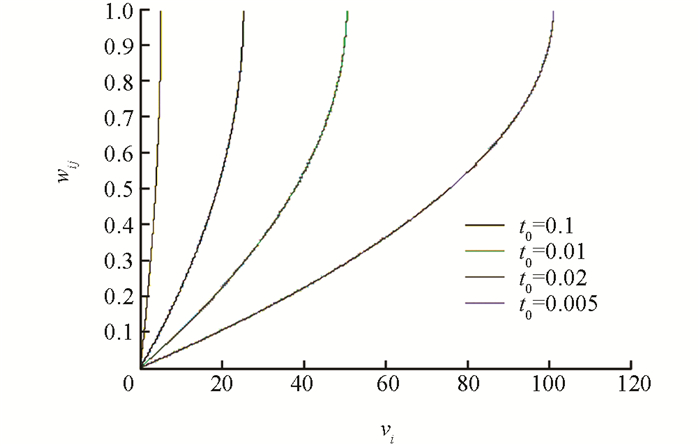
公式(13)中设定初始忆阻值为R_off，那么各交叉点的阻值变化ΔM_ij=R_off-M_ij.将式(11)和式(1)、式(2)做比较，可以得到，忆阻模糊神经网络的权值表达式为w_ij=-ΔM_ij/R_f，从图 11可以看出在不同时间电压激励下，只要电压不超过阈值电压，那么神经网络的权值小于等于1，这与模糊隶属函数的值小于1相类似，且从图中可以看出权值为单调递增函数.仿真参数为μ_v=10^-14 m²/(s·v)，D=10^-8 m，R_on=1 kΩ，R_off=100 kΩ.

为了验证所提系统的有效性，下面进行两个不同类型的应用.首先是对一个复杂的函数进行建模，这个函数常被用于许多相关模糊系统领域的检测基准^[15]；第二个应用就是模糊PID控制.所有的仿真采用的是MATLAB 2014版，仿真所选取的函数定义如下

这里采用未解释方差分数指数(FVU)来评估所得的结果，用F_FVU表示. F_FVU定义为

其中g(x_i，y_i)是由函数本身产生的值，$\mathop g\limits^ \wedge ({x_i}, {y_i})$是由文中所提的模糊推理系统所产生的值，n为测试数据的个数，F_FVU越小说明准确性越高.

公式(15)函数如图 12(a)所示，仿真采用图 7推理系统结构，当输入变量和交叉阵列都采用90根垂直线，代表 90个神经元，这样x和y最小分辨率即精度为$\frac{{\max (x)-\min (x)}}{N}$，根据训练数据对输入-输出的多少确定隐含层神经元的个数即水平线的条数(N)，若仿真采用400个输入-输出训练数据，那么就需要400个隐含层神经元.若输出端神经元个数为100即输出端采用100根垂直线，那么输出的精度可达到0.01.为了达到训练目的，输入数据x和y在输入空间均匀地选择，并用高斯隶属函数或者三角隶属函数模糊化，然后转化为与之对应的输入电压信号，将这些信号施加到与之对应的行和列，这将会在模块A、B、C上产生模糊关系.然后在输入端施加任意产生的10 000个测试信号(如果是精确数就用隶属函数将其模糊化)，最后将所得到的模糊数进行解模糊，就会得到如图 12(b)所示的结果.

表格1是在不同神经元个数下的FVU指数.首先构造交叉阵列推理系统，用90根垂直线分别代表x，y，用100根垂直线来表示z，可以推出x，y，z的最小分辨率分别为0.1，0.1，0.01.从表中可以看出通过增加神经个数，FVU指数逐渐趋于零，即精确度逐渐提高.

下面将所设计的推理系统用于基于模糊规格的PID控制，同样采用二输入单输出的控制对象.设被控对象为${G_p}(s) = \frac{{133}}{{{s^2} + 25s}} $，采样时间间隔为1 ms，采用z变换对其离散化得：

输入信号幅值为1.0的阶跃信号，根据经验可得模糊系统e、ec、k_p、k_i的模糊规则表，描述如下^[12]：

1. If(e is N) and (ec is N) then (k_p is N)(k_i is Z)

2. If(e is N) and (ec is Z) then (k_p is N)(k_i is Z)

3. If(e is N) and (ec is P) then (k_p is N)(k_i is Z)

4. If(e is Z) and (ec is N) then (k_p is N)(k_i is P)

5. If(e is Z) and (ec is Z) then (k_p is P)(k_i is P)

6. If(e is Z) and (ec is P) then (k_p is P)(k_i is P)

7. If(e is P) and (ec is N) then (k_p is P)(k_i is Z)

8. If(e is P) and (ec is Z) then (k_p is P)(k_i is Z)

9. If(e is P) and (ec is P) then (k_p is P)(k_i is Z)

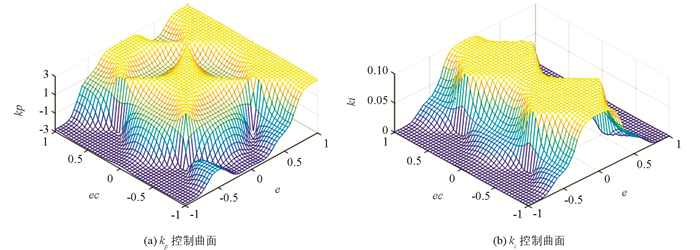
从此规则可以看出该控制系统采用的是P、I控制，首先在文章设计的模糊推理系统中构建模糊规则，然后就可以根据误差e和误差变化ec的范围得到k_p和k_i的控制曲面，如图 13所示.

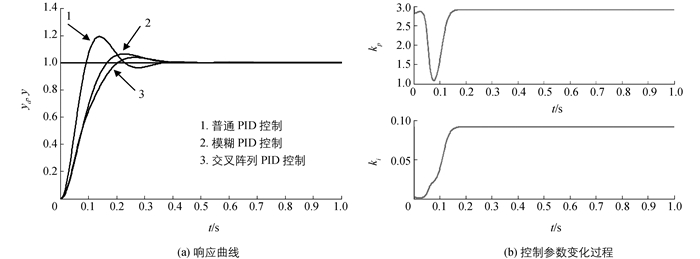
利用所设计的模糊系统进行P、I控制参数的整定.为了方便显示模糊规则的调整过程，取k_p和k_i初值为零，利用MATLAB进行仿真，我们可以得到如图 14的响应曲线和PID控制参数的变化过程.

图 14(a)中曲线1是普通PID控制曲线，初始参数k_p=0.3，k_i=0，曲线2是采用MATLAB模糊控制工具箱得出的控制曲线，其达到稳定的时间为0.4 s，曲线3是采用本文设计的忆阻器交叉阵列模糊PID控制器得出的响应曲线，可以看出该PID控制超调量明显降低，达到稳定时间为0.35 s. 图 14(b)是k_p和k_i控制参数随时间的变化曲线.值得一提的是本文设计的模糊PID控制器还具有一般模糊PID控制器达不到的纳米级尺寸，因此，有望实现成便携式模糊控制器.

本文首先分析了人工神经网络同模糊推理系统的关系，然后利用忆阻器交叉阵列结构设计了模糊神经推理系统，该系统摒弃了传统模糊神经网络繁琐的算法缺点，直接采用忆阻值的更新代替权值更新，为模糊神经网络的硬件实现提供了设计方案，其数值仿真和FVU评估验证了设计的推理系统的有效性和准确性.最后将其应用到工业模糊控制中，从仿真结果显示该控制器较传统PID控制器有诸多优势，为多变量和多维模糊控制器的设计提供了新的设计方案.因此，研究模糊控制器的硬件电路具有较高的理论价值和应用价值.