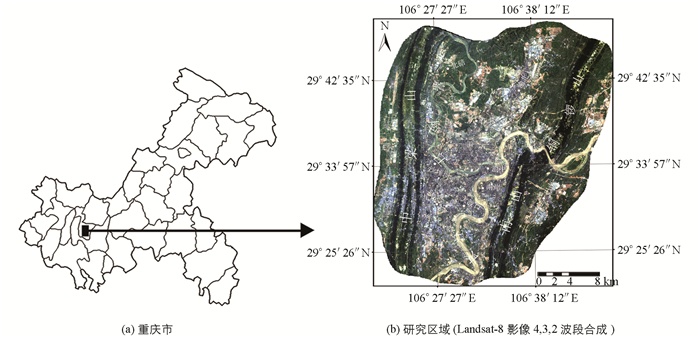
以重庆市主城区及周边区域为研究靶区，该研究靶区包含多条山脉和河流(图 1)，坐标：106.2°E-106.46°E，29.21°N-29.48°N，南北跨度约49 km，东西跨度约42 km，整体面积约1 614 km².海拔最高838 m，最低109 m，平均284 m.嘉陵江和长江贯穿于整个研究区域，且在渝中区交汇.中梁山、南山和铜锣山近似平行地分布于研究区域两侧.众多的山脉和河流使得研究区域形成一个多层次的复杂结构，另外，加速的城市化进程也使得研究区域中的热岛效应非常明显.

数据源为2013年6月16日过境的Landsat-8遥感影像，天气晴朗，成像清晰.完成图像几何校正，并将所有波段重采样到30 m分辨率.利用Landsat-8 TIRS数据，基于大气校正法反演地表温度.首先估计大气对地表热辐射的影响，随后利用公式(1)计算卫星传感器所接收到的热红外辐射亮度L_λ.

式中：ε表示地表比辐射率；τ表示大气在热红外波段的透过率；T_sruface表示地表真实温度(K)；L_upper和L_down分别表示大气向上和向下辐射亮度.然后利用公式(2)计算得到黑体热辐射亮度B(T_surface)，

最后利用普朗克公式(3)计算地表温度T_sruface^[12].

式中：对于TIRS Band10，K₁=774.89(Wm^-2sr^-1μm^-1)，K₂=1 321.08 K.

Matheron于1963年提出了半变异，将其定义为区域化变量增量平方的数学期望.本文的研究对象是温度，每一个象元温度可以被认为是受其位置影响的区域化变量，变量与位置之间的函数关系便可以用来描述地表温度的空间分布特征^[13].因此，地表温度的空间变异性可以用模拟的实验半变异函数来描述，定义为公式(4)：

式中：r(h)表示半变异函数值；Z(xi)表示区域化变量，即象元温度值；h为2个样本点的间隔距离；N(h)表示间隔距离为h的点对个数.

关于半变异函数有几个重要的参数：块金值、基台值、块金基台比、变程和分维数.块金值(C₀)，可以反映出随机变异的大小，当间隔距离h为0，半变异函数值却不为0时，说明具有块金效应，它表示由随机部分引起的空间变异；基台值(C₀+C)，可以反映变异幅度的大小；块金值与基台值的比叫做块金基台比，表示由随机因素引起的空间变异占总空间变异的比重；变程(A₀)是反映空间相关性的一个转变，表示从空间相关到空间不相关的一个转折点；分维数(D)可度量空间变异的复杂程度，它的值可以利用公式(5)并结合半变异函数值计算得出：

有些学者可能会假设地表温度在空间上的变化是均匀的，然后借助全向半变异函数定量地描述其空间异质性^[14].但在实际研究中，随着地理位置的变化，城市热岛的空间变异可能会变得非常复杂，尤其在本文所选的这种特殊山地城市(重庆市)中，很有可能在不同方向或者不同尺度呈现出不同程度的变异.因此，本文在不同方向和不同尺度2个方面，借助全向及各向实验半变异函数全面刻画重庆市热岛的空间异质性，并挖掘其背后的驱动原因.

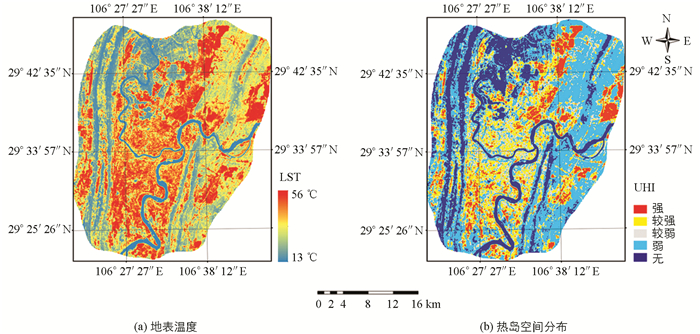
反演得到的地表温度如图 2(a)所示.温度范围为13 ℃~56 ℃，平均温度为23 ℃.本文进一步借助热场变异指数将地表温度标准化处理.热场变异指数(HI)可由公式(6)计算得到.

式中：T_s表示象元温度值，T_mean表示平均温度值.热场变异指数是以地表温度为基础的相对变量，数值越高意味着热岛效应越明显，可以较好地描述城市热岛效应^[15].本文将热场变异指数划分为5个等级^[16]：HI≤0.1表示无热岛效应；0.1＜HI≤0.3表示弱的热岛效应；0.3＜HI≤0.4表示较弱的热岛效应；0.4＜HI≤0.6表示较强的热岛效应；HI＞0.6表示强的热岛效应.划分等级后的热岛空间分布如图 2(b)所示.

从图 2可以看出，城市热岛整体呈现出带状分布，热岛的中心主要位于3条山脉中间人群和建筑比较密集的大渡口区、渝中区等.但可能由于河流对于热岛所起的部分缓解作用，导致主城区的主要热岛效应呈较强而非强的状态.中梁山、铜锣山以及长江、嘉陵江所分布的区域呈弱热岛或者无热岛效应.由此看出，研究区域中不同地理要素的空间分布对城市热岛的空间分布产生了明显的影响，而由于研究区域中各种地理要素的空间位置错综复杂，这也导致城市热岛呈现出复杂的空间异质性.

采用地统计软件GS+7.0模拟不同方向和不同尺度下的城市热岛实验半变异函数，综合探究研究区域中城市热岛的空间异质性.

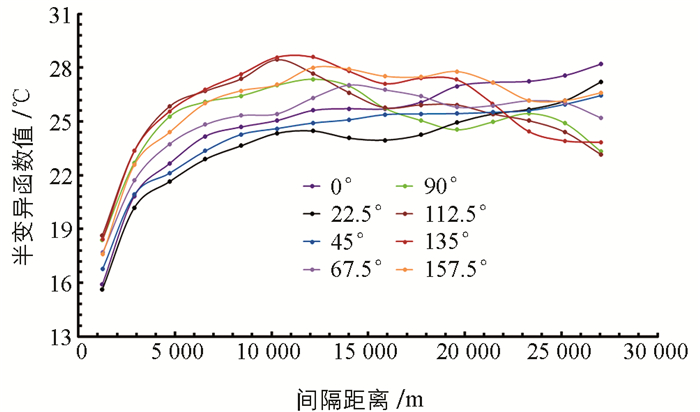
参考研究区域中不同地理要素的分布情况，本文拟从8个方向分析城市热岛空间变异的各向异性，即0°，22.5°，45°，67.5°，90°，112.5°，135°和157.5°(正北方向为0°，顺时针旋转).根据相关系数较大、残差较小的原则，通过模拟各方向上的实验半变异函数，发现计算得到8个方向上城市热岛半变异函数的最优拟合模型都为指数模型，各方向上实验半变异函数的散点图如图 3所示.

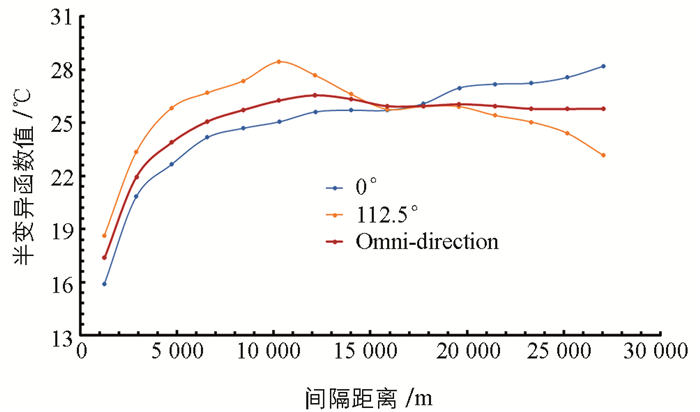
从图 3中可以看出，不同方向的变异函数曲线各有不同，表明城市热岛在各方向上的变异存在明显的差异.大致可以将其分为2类：第一类0°，22.5°，45°和67.5°这4个方向上的函数值波动平稳，呈持续增长的趋势；第二类90°，112.5°，135°和157.5°这4个方向上的函数值波动较大，呈一种先增大后减小的趋势.为了更加明显地展示这2类变异函数的差异，本文从这两大类中提取出差异最大的2个方向，分别为22.5°和112.5°方向，结果如图 4所示.

根据半变异函数的计算公式(4)可知，函数值在很大程度上依赖于各方向上间隔距离为h的像素点对的差值.而在整个研究区域，城市建筑、主要山脉以及河流的分布大致都沿着0°~22.5°方向，也就说在这些方向上，随着间隔距离h的逐渐增大，点对中像素点之间的差值的变化是稳定的，导致在这些方向上半变异函数曲线的变化较为平稳；相反，在与其相垂直的90°~112.5°方向上，由于山脉的阻隔，高低温交错分布，导致其随着间隔距离h的增大，点对温度差值的变化随机性较大，因此，在这些方向上半变异函数曲线的波动较明显，且复杂.

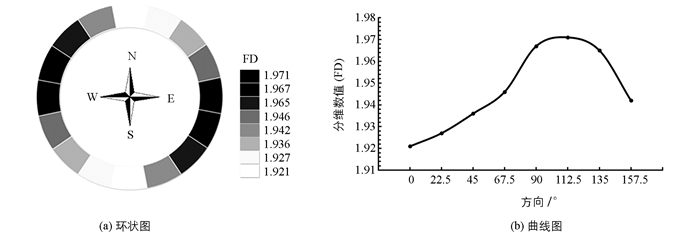
以上实验结果证明，各向半变异函数在不同方向上的差异具有统计学意义，最大的差异出现在22.5°和112.5°方向.为了进一步验证城市热岛在不同方向上空间变异的差异性，本文对8个方向上的分维数进行计算，实验结果如图 5所示.

从图 5中可以看出，在0°方向上，分维数为最小值1.921，而当方向旋转到112.5°时，分维数达到最大值1.971，曲线整体呈现出一个先升高后降低的变化趋势.各向分维数值的大小可以表示该方向上空间变异的复杂程度，也就证明了研究区域中城市热岛的空间分布存在明显的各向异性，而且在0°方向上变异最简单，随着方向的旋转，变异的复杂度在逐渐增大，旋转到112.5°方向时变异的复杂度达到最大.此结果与前文中各向半变异函数所表现出的结果相一致，即在0°~22.5°方向上呈现出简单的变异性，在90°~112.5°方向上呈现出复杂的变异性.

各向空间异质性分析证明研究区域中城市热岛的空间异质性存在明显的各向异性，且不同地理要素的空间分布对热岛的空间异质性造成了很大的影响.在本文的研究区域中，有3种明显的地理要素，山脉、河流和城市建筑.因此，为了进一步探究这3种地理要素对于热岛空间变异所产生的影响，本文参考数学中减少变量的方法，依据3种地理要素的分布划分出3种尺度，尝试从多尺度角度探测研究区域中热岛的空间变异特性.

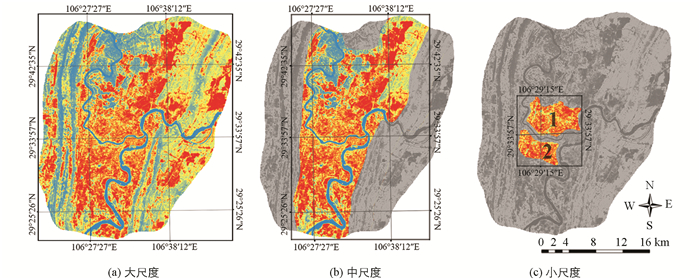
实验中，划分出3种尺度，分别为大、中、小，如图 6所示.大尺度(L)包括整个研究区域，目的是探测多因素下城市热岛的空间变异(图 6(a))；中尺度(M)包括嘉陵江和长江，以及城市建筑区域，目的是探测除山脉以外的多因素下城市热岛的空间变异(图 6(b))；小尺度仅包括建筑区域，目的是探测建筑对城市热岛空间变异的影响，为了避免城市建筑的区域性差异对实验结果的影响，在小尺度下共选取了2个样本区域(c₁，c₂)进行实验(图 6(c)).

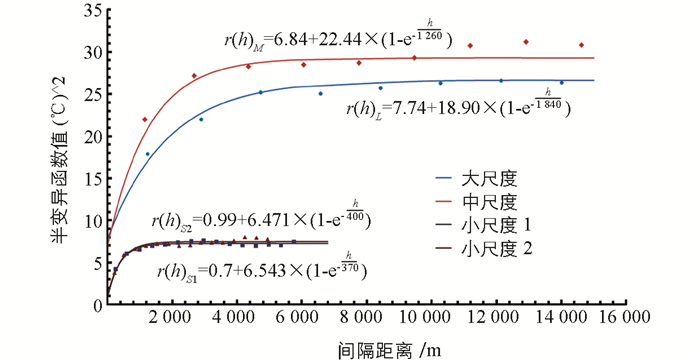
模拟计算各尺度下的全向半变异函数，宏观上假设城市热岛在空间上的变化是均匀的^[14].依据决定系数最大、残差最小这一规则^[17]，计算得到的最优拟合模型为指数模型，其它模型参数如表 1所示，各模型拟合曲线如图 7所示.

从表 1可以看出，相关系数R²均大于0.8，多数处于0.93以上，表明拟合效果较好，可以用来描述各尺度下的空间变异性.

在大尺度下半变异函数表现出了块金效应，块金值为7.74.通常，出现块金效应有2种原因：①存在更小尺度上的变异性；②样本分析中存在误差.本文为第一种原因，表明存在小尺度上的变异.基台值为26.64，反映出其空间变异的幅度.块金基台比(块金值与基台值的比值)可以反映系统变量空间相关性的程度，通常，块金基台比小于25%表示强烈空间自相关，大于75%表示空间自相关性比较弱.本文块金基台比为29.05%，表明整个研究区域城市热岛的空间自相关性处于较强的水平.之外还发现，随着尺度的减小，块金值在逐渐减小，块金基台比也在逐渐减小.结合图 7可以更加直观地看出各尺度下变异函数之间的3个明显的异同点：第一点：2个小尺度下的实验半变异函数曲线几乎重叠；第二点，大尺度和中尺度下的块金值和基台值差异较小；第三点，小尺度下的基台值近似等于大尺度和中尺度下的块金值.

可见，对研究区域中热岛的空间异质性进行全方位的分析，可以挖掘不同地理要素对于城市热岛空间变异所产生的影响以及各影响力之间的关系.

本文尝试基于半变异函数分析城市热岛的空间异质性，并以重庆市为实验区域，从多方向和多尺度两方面刻画重庆市城市热岛的空间异质性，并挖掘其背后的驱动原因.

研究表明，重庆市城市热岛空间格局复杂，但整体的空间自相关性较强，整体呈带状分布，集中于3条山脉中间人口和建筑的密集区域，这与LUO等^[16]对2013年的重庆市热岛研究所得出的描述相一致.通常，许多学者在分析时都假设城市热岛空间结构或者变异在各向是相同的，如陈公德等^[14]采用全向半变异函数对上海市的城市热岛空间结构进行分析.但从本文的各向半变异函数和各向分维数的表现来看，重庆市热岛空间变异的各向差异有统计学意义，具体表现在所选8个方向上的半变异函数曲线各不相同，且大致分为2类：一类为波动稳定，保持持续增长趋势；另一类为波动较大，变化趋势复杂.进一步通过各向分维数来验证热岛空间变异的各向差异，分维数同样以较大的波动表现出明显的差异，且最大的差异为互相垂直的0°~22.5°和90°~112.5°这2组方向.这与陈公德等^[14]的假设有所差异，这是因为重庆市为山城，研究区域中包含多条明显的山脉，在热岛整体空间分布的研究中证明山脉、河流区域呈现明显的无热岛或者低热岛效应，这点与学者们分析出的植被、水体覆盖区域热岛效应弱的结论相一致^[18].除此之外，最重要的是几条主要山脉的延伸方向恰为0°~22.5°，而宏观上热岛的整体分布带也是沿着该方向分布.因此，由于山脉对于热岛空间分布的阻隔，导致其在与山脉相垂直的方向上空间变异最为复杂，而在延伸方向上最为简单，从而表现出各向异性.所以，在这种分布着多种复杂地理要素的研究区域中分析城市热岛空间异质性时，需要参照具体的研究区域，考虑热岛在各向所表现出来的差异，从而描述其空间异质性.

在分析热岛的时候，许多学者都会提到尺度效应，如时间尺度^[19]和空间尺度^[16]等.在空间尺度上，常基于分辨率进行尺度划分.但本文研究区域中热岛的分布存在很多零碎的斑块状数据，如果重采样低分辨率尺度，可能会造成部分较小热岛斑块信息的丢失.因此，为了探究研究区域中不同地理要素对于热岛空间异质性的影响，本文综合考虑研究区域中存在的3种明显的地理要素，参考数学上常用的减少变量的思想，从整个研究区域中分割出3种范围尺度，逐一减少3种主要的地理要素的影响，从而探究不同地理要素的空间分布对于热岛空间变异所造成的影响.研究表明，在较大尺度(大尺度和中尺度)上半变异函数所表现出来的空间变异是不完全的，存在隐藏的变异未表现出来，产生了块金效应，块金值为7.74和6.84；而小尺度上的块金值仅为0.7和0.99，说明结构性引起的变异占比大于90%，整体结构比较完整地表现了出来.同时，通过综合对比各尺度下的块金值、基台值，揭示了3种主要地理要素(山脉、河流和城市建筑)对于城市热岛空间变异所产生的影响以及各影响力之间的关系，发现在某些特殊尺度下，山脉和河流对热岛所引起的变异较为相似，而且在较大尺度下隐藏的变异是由城市建筑引起，而城市建筑引起的热岛空间变异性是较稳定的，可以被小尺度下的变异函数很好地表现出来.

综上，本文从多向和多尺度描述了研究区域(重庆市)城市热岛的空间异质性，并结合实际地理要素，挖掘了驱动这种空间异质性形成的三大主要因子，以及各因子对热岛空间异质性所产生的影响和影响力之间的关系.但实际上，对热岛空间变异造成影响的因素远不止这3种，由于数据原因，无法分析在更小尺度上才能描述出来的因子对热岛空间异质性所造成的影响，这点还有待于进一步研究.