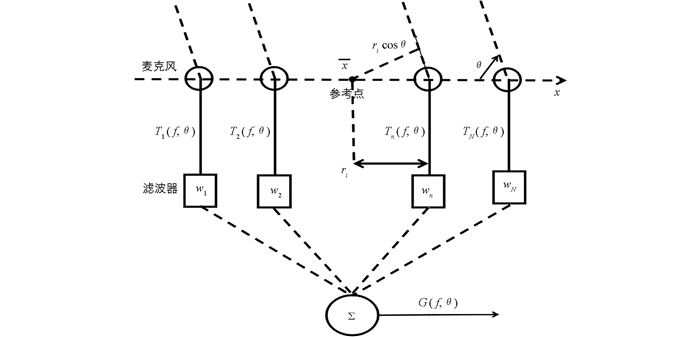
我们考虑一个含N个元素的麦克风阵列.如图 1所示为远场情形下的麦克风阵列结构图，对于每一个麦克风，后面接一个长度为L的有限脉冲响应(FIR)滤波器，那么麦克风阵列的频率响应函数为

其中，f是信号频率，R_i(f)表示第i个麦克风后面的FIR滤波器的频率响应，即

其中，w_i为有限脉冲响应滤波器的系数，且

这里j是虚数单位，g₀(f)表示滤波器的延迟，f_s为抽样频率.

在远场环境下，麦克风阵列的传递函数为

其中

且r_i是第i个麦克风到参考点位置的距离；c是语音在空气中的传播速度.公式(2)表示频率为f，入射方向为θ的信号相对于参考点的频率响应的变化.那么麦克风阵列的实际响应函数为

在实际应用中，我们可以规定通带区域和阻带区域，然后目标响应函数可表示为

其中，G_d(f，θ)是定义在Ω=Ω_p∪Ω_s这个区域上的；Ω_p是通带区域；Ω_s是阻带区域；τ_L表示的是与L相关的延迟参数，且τ_L∈[0，L-1]，它与系统的相位有关.那么，麦克风阵列的波束形成的设计问题就可转化为滤波器的系数设计，使得输出的实际响应函数G(f，θ)逼近目标响应函数G_d(f，θ).采用最大值误差时，目标函数表示为

这里ρ(f，θ)为正的权重函数，它衡量着通带区域与阻带区域的重要性.

令w=[w₁，w₂，…，w_N]^T，波束形成设计问题就是找出滤波器系数w∈R^NL，使得目标函数(5)的值达到最小，这个问题可以等价为一个半无限规划问题，如下所示：

其中

可以看出问题(6)是凸的，它的最优解是能保证的，该问题可以通过一些半无限规划、二阶锥规划或正半定规划的方法进行求解.

对于问题(6)的设计，如果滤波器的长度比较小时，波束形成问题的性能比较差.为了得到一个较好的性能，通常需要把滤波器的长度设得比较大，然而当滤波器长度变大时，在通带区域与阻带区域的端点处会出现振荡很大的现象，这种现象称为吉布斯现象.一般来说，吉布斯现象是在反傅里叶变换的计算过程中，用有限项近似无限项，从而丢失原信号中的高频部分所致.

通常，由于目标函数只考虑了通带区域和阻带区域，实际响应函数在过渡带区域的性能值是不受影响的，但是由于模型具有一定的不确定性和一些随机干扰性，如麦克风的位置测量不精确，声音速度的变化等.因此，实际响应函数的幅度值在通带区域或阻带区域会发生一定的变动，这导致过渡带区域会出现严重的振荡现象，使得原波束形成设计的性能变得非常差.

由于实际响应函数在所有区域上都有定义，但目标响应函数只定义在通带区域和阻带区域.因此，实际响应函数在过渡带区域振荡是因为目标响应函数的定义不完整，在过渡带区域无法控制.那么，为了加强波束形成设计的鲁棒性，过渡带区域上最好有光滑的实际响应函数，这就需要在过渡带区域也先定义一个平滑的目标响应函数.

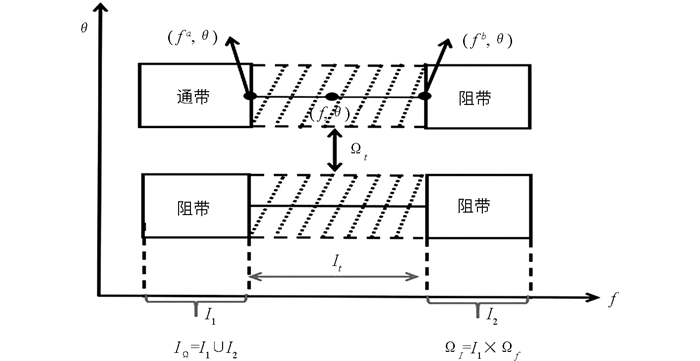
考虑区域Ω，它可以按照频率分解为

其中对每一个频率f，Ω_f是Ω中相对应于f的空间域.考虑到可能存在某些频率f使得Ω_f为空集，我们记I_Ω为[0，f_s/2]中所有Ω_f≠Ø的频率f的集合.那么过渡带区域相对应的频率在区间[0，f_s/2]里，但不在集合I_Ω里.

图 2所示为过渡带区域的描述图.我们把频率所对应的过渡带区域的集合记为I_t，那么I_t×Ω_f就是过渡带区域，记为Ω_t.当f∈I_t时，在过渡带区域I_t×Ω_f里定义一个平滑的目标响应函数，并且实际响应的性能在研究区域内不受影响.因此对于给定一个点(f，θ)∈I_t×Ω_f，我们令I_t是由端点属于I_Ω的若干个开区间组成.假设(f，θ)两边的2个端点记为(f^a，θ)和(f^b，θ)，那么通过在这2个点做一个插值函数，我们就可以在(f，θ)里定义一个新的目标响应函数值.为了保证其光滑性，插值函数需要保证目标响应函数是连续的.插值函数的选择是非常多的，最方便的选择就是线性插值函数，即

由于权重函数可以衡量频域空间的重要性，因此我们需要在过渡带区域定义权重函数，一个恰当的权重函数值在过渡带区域中应该不大于研究区域Ω的值.对于∀f∈I_t，我们通过在(f，θ)里定义目标响应函数，则可建立一个光滑过渡带设计问题

其中

该问题等价于优化一个最大化目标函数

光滑过渡带设计问题(8)的约束比问题(6)的约束多，当给定一个滤波器长度L时，问题(8)的最优解必定是问题(6)的可行解.因此光滑过渡带设计问题的最优解不会优于问题(6)的最优解，但是在某些情况下，问题(8)的最优解可以达到问题(6)的最优解.

当滤波器长度为L时，记z_L^*和z_L^*′分别是问题(6)和问题(8)的最优性能值，取$\inf\limits _{L} z_{\mathrm{I}}^{*}$和$\inf\limits _{L} z_{\mathrm{L}}^{*}$分别是这2个问题的性能极限值.令w^*mL是滤波器长度为L时问题(8)的最优解，对于问题(8)，记

令w^*oL是滤波器长度为L时问题(6)的最优解，对于问题(6)，记

我们需要比较问题(6)和(8)在研究区域Ω中最优性能值的极限，即需要比较$\inf\limits _{L} z_{L}^{*}$和$\inf\limits _{L} z_{L}^{* \prime}$.由问题(6)的最优性和等式(9)可知

若满足一些约束条件，(14)和(15)的不等式将变成等式.首先，我们给出以下引理和定理.

引理1  若$z^{* t}(L) \leqslant z^{* s}(L)$，则$z^{*}(L)=z^{* \prime}(L)$.

证  因为问题(8)的最优解w^*mL比w^*oL好，即

则由(14)和(16)式有z^*(L)=z^*′(L).

定理1  在求解出滤波器系数w的条件下，假设R^*oL是一致有界的，即∃M＞0，对任意的L和任意的f∈Ω_t，有R^*oL≤M.若∃ρ₀＞0，且权重函数在过渡带区域满足ρ(f，θ)≤ρ₀，则

证  对任意滤波器长度L，目标函数在过渡带区域可表示为

设ρ₀=(z_L^*/D)^1/2，则

则由引理1，有

上式对L取下确界，可得(17)式.

一般地，当滤波器长度L固定时，z^*s′(L)和z^*s(L)的下确界达不到，但肯定存在一个子序列{L^(k)：k=1，2，…}，使得z^*(L^(k))和z^*s′(L^(k))的极限分别为z^*s(L)和z^*s′(L)的下确界.为了方便起见，不妨假设{L：L=1，2，…}自身是收敛的子序列，则有

定理2   假设(18)式的条件成立，则对∀ε＞0，存在一个滤波器的长度为L^′，当滤波器长度为L^′，并且滤波器系数为w^L'时，使得

其中，z^s(L)和z^t(L)是(12)式和(13)式中w^*oL被w^L代替后的取值.

证  对∀ε＞0，存在滤波器的长度L₀，使得当∀L₁$ \ge $L₀时，有

为了证(19)式，分两种情况：

第一种情况：假设z^*s′(L₁)≤z^*(L₁)，取L'=L₁，设w^L'=w^*mL'，则

则(19)式成立.

第二种情况：z^*s′(L₁)＞z^*(L₁)，记问题(6)和(8)的最优解分别为w^*oL₁和w^*mL₁，相应的频率响应函数分别记为R^*o(f)和R^*m(f)，则定义一个新的频率响应函数为

其中，g是一个连接I_t\I'和I_Ω的过渡函数，I'∈I_t，并且包括了I_Ω端点附近的部分.令f^a，f^b是I_Ω的端点，并且I_t=(f^a，f^b).又z^*s′(L₁)＞z^*(L₁)，则

由于函数H关于f是连续的，那么存在η＞0，使得(f^a，f^a+η)∈I_t，有

其中，I'=(f^a，f^a+η)，为了保证R(f)的连续性，则函数g应为线性函数，故g定义为

对函数g(R^*o(f)，R^*m(f))，当f∈I'时，记

则新的频率响应函数R(f)满足

由于R(f)是连续的，因此可通过反傅里叶变换计算相应的系数w'.记相应的频率响应函数为R^L'(f)，由于目标函数关于频率响应函数是连续的，则可取滤波器的长度L'充分大，使得R^L'(f)非常接近R(f)且满足

结合(20)式和(23)式，则(19)式可证.

故通过定理2可知，当L增大时，问题(8)的实际响应均满足研究区域和过渡带区域.

本文麦克风阵列的光滑过渡带区域设计的例子中，麦克风线性阵列的位置为{-0.2，-0.15，-0.10，…，0.10，0.15，0.2}，它共包括了9个麦克风.这里延迟参数为τ_L=(L-1)/2，声音传播的速度为c=340.9 m/s，抽样频率为f_s=8 kHz，权重函数恒为ρ(f，θ)=1.参考点设定为麦克风阵列的中心位置，即将第5个麦克风作为参考点.

阻带区域设定为

通带区域设定为

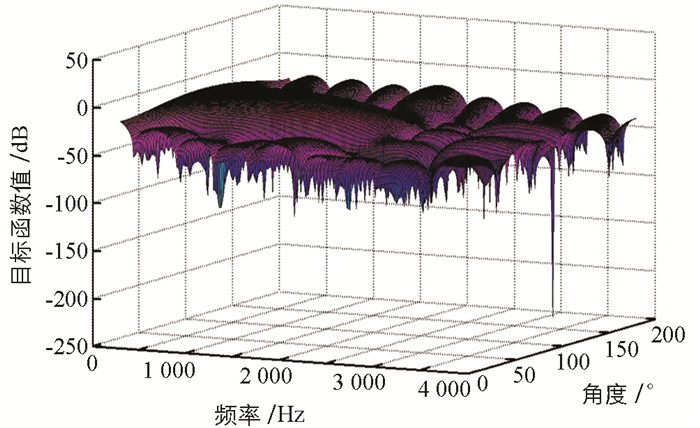
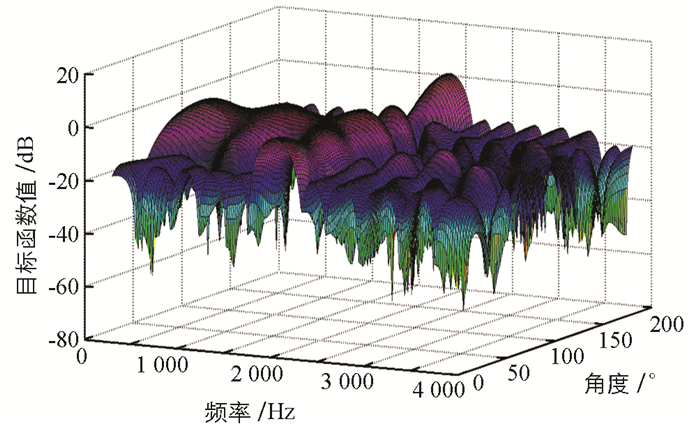
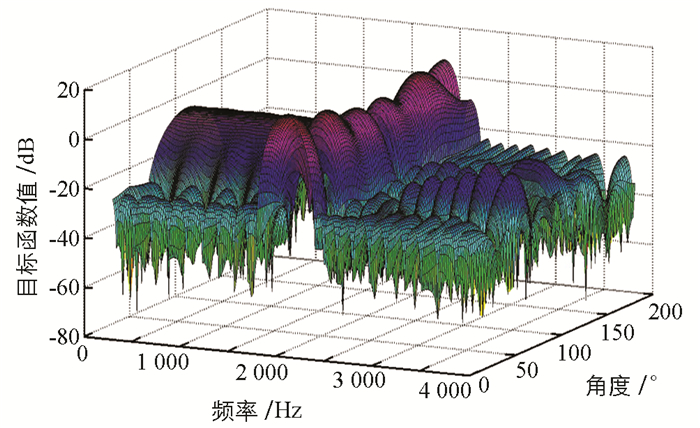
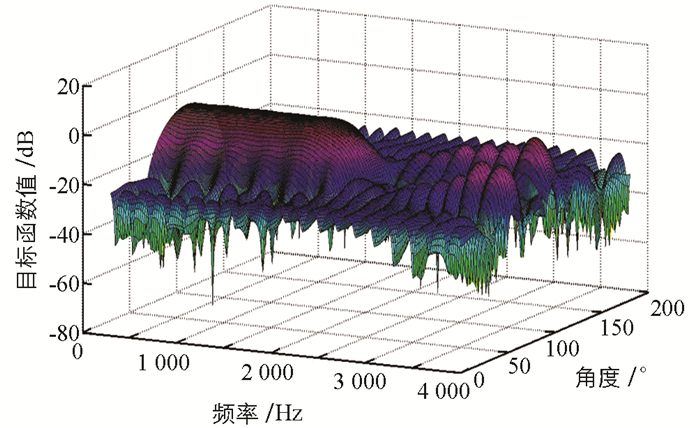
由图 3~图 5可知，当滤波器的长度为10，20，40时，可以求出问题的最优性能值分别为-6.534 7 dB，-12.639 2 dB，-21.411 2 dB.当滤波器的长度比较大时，波束形成的性能不断增强，然而在通带区域与阻带区域的端点处出现振荡很大的现象.由图 3可见，当滤波器长度为10时，几乎没有振荡；由图 4可见，当滤波器长度为20时，出现了一点振荡现象；由图 5可见，当滤波器长度比较大时，实际响应函数在过渡带区域的吉布斯现象非常明显.

为了消除吉布斯现象，需要建立光滑过渡带设计问题.为此，我们在过渡带区域定义一个光滑目标响应函数

其中

接着对光滑过渡带设计问题求解，求出滤波器长度为40的最优性能值为-21.083 8 dB，与波束形成设计问题中滤波器长度为40的最优性能值-21.411 2 dB非常接近.当滤波器长度为40时，它的实际响应函数如图 6所示，可以发现它在过渡带区域非常平稳光滑，并且吉布斯现象得以消除.

本文研究波束形成问题的光滑过渡带设计问题，得出以下结论：

1) 滤波器长度增大时，远场麦克风阵列波束形成问题在过渡带区域出现振荡现象.

2) 对区域进行分解，采用了插值函数，引进了目标响应函数在过渡带区域的平滑定义，从而建立了一个改进的波束形成设计问题，消除了过渡带区域的振荡现象.

3) 当滤波器长度逐渐增大时，波束形成设计与光滑过渡带设计的最优性能值的变化很逼近.