Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2018 Volume 40 Issue 8
Article Contents
Previous Article Next Article

Yong-li ZHANG, Wei HUANG, Yan-jun ZHANG. Calculation of Three-Dimensional Surface Settlement Caused by Tunnel Excavation Under Sloping Ground[J]. Journal of Southwest University Natural Science Edition, 2018, 40(8): 147-153. doi: 10.13718/j.cnki.xdzk.2018.08.020
Citation: Yong-li ZHANG, Wei HUANG, Yan-jun ZHANG. Calculation of Three-Dimensional Surface Settlement Caused by Tunnel Excavation Under Sloping Ground[J]. Journal of Southwest University Natural Science Edition, 2018, 40(8): 147-153. doi: 10.13718/j.cnki.xdzk.2018.08.020
shu

Calculation of Three-Dimensional Surface Settlement Caused by Tunnel Excavation Under Sloping Ground

  • 1.

    Liaoning Technical University, Fuxing Liaoning 123000, China

  • 2.

    STATE GRID Nanchang Power Supply Company, Nanchang 330000, China

More Information
  • Received Date: 29/01/2018
    Available Online: 20/08/2018

  • MSC: U459.3

  • In order to develop a good calculation method of ground settlement induced by tunnel excavation under inclined surface, considering the influence of inclined surface on the depth of the tunnel, a tunnel excavation model under inclined ground and a three-dimensional excavation model for unit excavation are established. Formulas for calculating the surface subsidence caused by the excavation of a three-dimensional tunnel under an inclined surface are derived, using the theory of stochastic medium. The accuracy of the calculation method is proved by the comparison and verification of the monitoring data and the calculation result. In the end, a comparative analysis is made of the surface inclination angles, the result of which shows that the greater the inclination angle of the surface, the more obvious the uneven settlement of the surface.
  • 加载中
  • [1] SAGASETA C. Analysis of Undrained Soil Deformation Due to Ground Loss[J]. Géotechnique, 1988, 38(4):647-649. doi: 10.1680/geot.1988.38.4.647

    CrossRef Google Scholar

    [2] LOGANATHAN N, POULOS H G. Analytical Prediction for Tunneling-Induced Ground Movements in Clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(9):846-856. doi: 10.1061/(ASCE)1090-0241(1998)124:9(846)

    CrossRef Google Scholar

    [3] VERRUIJT A, BOOKER J R. Surface Settlements Due to Deformation of a Tunnel in an Elastic Half Plane[J]. Geotechnique, 1996(46):753-756.

    Google Scholar

    [4] VERRUIJT A. A Complex Variable Solution for a Deforming Circular Tunnel in an Elastic Half-Plane[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21(2):77-89. doi: 10.1002/(ISSN)1096-9853

    CrossRef Google Scholar

    [5] 晏莉, 阳军生, 刘宝琛.浅埋双孔平行隧道开挖围岩应力和位移分析[J].岩土工程学报, 2011, 33(3):413-419.

    Google Scholar

    [6] 张彬, 廖连烨, 朱凤薇.地铁施工考虑流固耦合效应对地表沉降影响[J].辽宁工程技术大学学报(自然科学版), 2017, 36(1):52-56. doi: 10.11956/j.issn.1008-0562.2017.01.010

    CrossRef Google Scholar

    [7] 白光宇, 张德强, 张进德, 等.山区开采沉陷地表移动变形规律[J].辽宁工程技术大学学报(自然科学版), 2017, 36(7):684-688.

    Google Scholar

    [8] 邱明明, 杨果林, 魏赛赛, 等.大跨度公路隧道施工力学响应数值试验研究[J].西南大学学报(自然科学版), 2017, 39(12):170-178.

    Google Scholar

    [9] LITWINISZYN J. The Theories and Model Research of Movements of Ground Masses[C]//Proceedings of the European Congress on Ground Movement. University of Leeds, 1957: 202-209.

    Google Scholar

    [10] BAOCHEN L, DEZHANG L. The Application of Stochastic Medium Theory to the Problem of Surface Movements Due to Open Pit Mining[J]. Chapter, 1982, 16:407-416.

    Google Scholar

    [11] BAOCHEN L. Stochastic Medium Theory and Its Application in the Settlement Problems[J]. Comprehensive Rock Engineering, 1993, 4:780-816.

    Google Scholar

    [12] YANG J S, LIU B C, WANG M C. Modeling of Tunneling-Induced Ground Surface Movements Using Stochastic Medium Theory[J]. Tunnelling and Underground Space Technology, 2004, 19(2):113-123. doi: 10.1016/j.tust.2003.07.002

    CrossRef Google Scholar

    [13] 黎新亮. 浅埋暗挖隧道地层变位随机介质理论分析及控制技术研究[D]. 北京: 北京交通大学, 2008.http://cdmd.cnki.com.cn/Article/CDMD-10004-2008078525.htm

    Google Scholar

    [14] 施成华, 彭立敏.随机介质理论在盾构法隧道纵向地表沉降预测中的应用[J].岩土力学, 2004(2):320-323.

    Google Scholar

    [15] MENG F, ZHANG J S, LIU H Y. Analysis of Ground Movement in Pile Driving Based on Stochastic Medium Theory[J]. Applied Mechanics and Materials, 2013, 438:1404-1408.

    Google Scholar

    [16] YANG X L, WANG J M. Ground Movement Prediction for Tunnels Using Simplified Procedure[J]. Tunnelling and Underground Space Technology, 2011, 26(3):462-471. doi: 10.1016/j.tust.2011.01.002

    CrossRef Google Scholar

    [17] 程波.抛填深埋暗挖地铁隧道施工技术研究[J].重庆理工大学学报(自然科学版), 2017, 31(9):84-89.

    Google Scholar

    [18] ZOU J F, ZHANG Y J, DAN H C. Three-Dimensional Ground Settlement Induced by Metro Tunnel Excavation Considering the Influence of Group Piles[J]. Mathematical Problems in Engineering, 2016:1-13.

    Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(10)  /  Tables(1)

Export Citation
PDF
XML

Article Metrics

Article views(3219) PDF downloads(446) Cited by(0)

Access History

Other Articles By Authors

Calculation of Three-Dimensional Surface Settlement Caused by Tunnel Excavation Under Sloping Ground

  • Received Date: 29/01/2018
  • Available Online: 20/08/2018

Abstract: In order to develop a good calculation method of ground settlement induced by tunnel excavation under inclined surface, considering the influence of inclined surface on the depth of the tunnel, a tunnel excavation model under inclined ground and a three-dimensional excavation model for unit excavation are established. Formulas for calculating the surface subsidence caused by the excavation of a three-dimensional tunnel under an inclined surface are derived, using the theory of stochastic medium. The accuracy of the calculation method is proved by the comparison and verification of the monitoring data and the calculation result. In the end, a comparative analysis is made of the surface inclination angles, the result of which shows that the greater the inclination angle of the surface, the more obvious the uneven settlement of the surface.

    HTML

  • 随着我国能源消耗日益增长，自然资源丰富区域地下大范围被采空.同时，地铁和高速公路的快速发展，导致大量隧道开挖，地下工程开挖时会导致地面发生不均匀沉降，尤其是对于斜坡地面，严重的不均匀沉降会影响原有基础设施和建筑物的使用性和安全性.针对隧道施工和地面沉降计算，国内外很多研究学者对此做出了大量研究，例如，Sagaseta[1]提出了地层损失概念，通过镜像源汇法简化了半空间隧道开挖的弹性解，得到了弹性假设条件下的位移及应力解答.同时，Loganathan和Poulos等[2-3]在他的研究基础上，修正了计算方法得到垂直位移准确的计算公式. Verruijt等[4]人提出了复变函数法，建立了弹性模型，推导出了圆形隧道发生均匀收缩时半无限空间内围岩解析解并进行了数值分析.晏莉[5]等通过应力函数法对双孔平行有压隧道围岩位移进行了讨论.张彬等[6-8]运用有限元方法，考虑流固耦合效应模拟了地铁隧道施工地表竖向位移等值线，并在流固耦合作用下研究了不同地下水位高度的隧道施工对地表沉降的影响.但是这些计算方法比较复杂，并且在计算过程中需要提供大量的岩土参数，导致地表沉降的计算难度大大提升.

    针对岩土体参数复杂和获取难度大的特点，Litwiniszyn[9]针对采煤岩层和地表移动规律问题提出了随机介质理论，大大简化了计算过程，为地表沉降研究做出了重大的贡献.该理论经过我国刘宝琛等[10-15]研究和推广之后在岩土工程界得到了广泛应用.例如，刘宝琛等运用随机介质理论深度研究了煤矿开挖等情况下引起的地表下沉问题，杨小礼等[16-17]人研究了单孔隧道和双孔隧道开挖引起的地表竖向沉降和水平位移，并且分析了不同隧道深度和角度对沉降的影响.邹金峰等[18]针对桩基作用下的三维地表预测进行了相关的研究.但是在已有的关于随机介质理论研究中大多数是针对平面内水平地表沉降计算，针对三维倾斜地表研究却并不多见.本文基于随机介质理论，建立了倾斜地表下三维地表沉降计算模型，并且得出了沉降解析解.

1.   计算原理与模型

    1.1.   计算模型

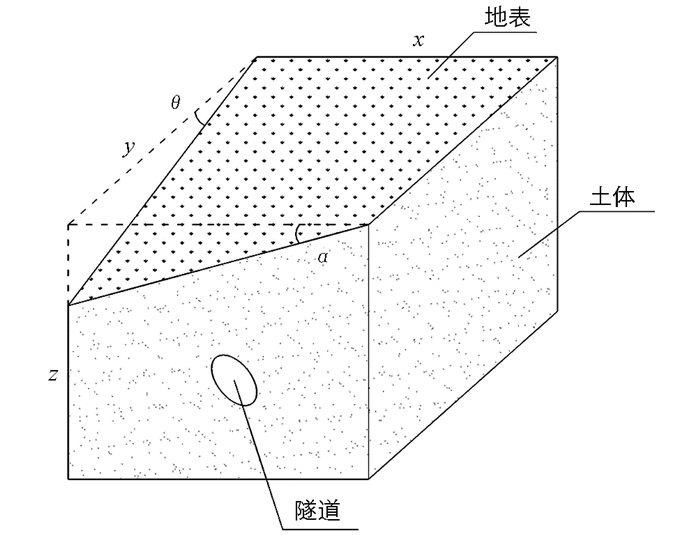
  • 在均质的、各向同性的和不可压缩的土体中，开挖一个直径不变的隧道，隧道开挖时可及时采取支护措施阻止隧道坍塌，但是隧道在支护后仍会沿半径方向发生收缩，引起地表沉降.基于上述分析，本文建立了倾斜地表情况下三维隧道开挖模型和地表沉降计算模型，以竖直向下为z轴正方向，隧道开挖方向为y轴正方向，x轴垂直y和z轴，如图 1所示.

    • 1.2.   计算原理

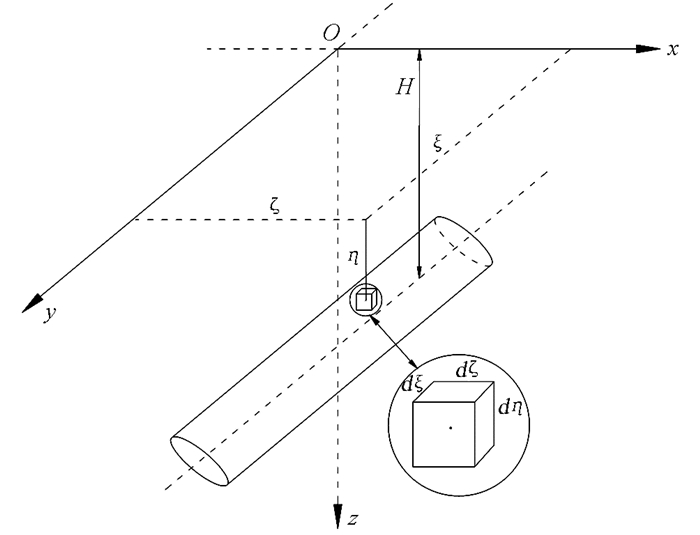
  • 根据随机介质理论基本原理可知，隧道开挖过程可分解为无数个微小单元体开挖，地表位移可假定等于无数个微小单元体开挖形成的地表位移的线性叠加.本文计算时引入单元体开挖时地表沉降计算方法，单独计算地表每一点位移，计算过程中采用双坐标系，即为全球坐标系(x，y，z)和当地坐标系(ξ，ζ，η)，坐标系以竖直向下为z轴(η轴)正方向，如图 2所示.隧道开挖时土体的下沉量用函数W(z，x，y)[17]满足：

    式中：B11，B12，B22，A1，A2，N是取决于介质结构特性的参数.

    结合单元体开挖边界条件，根据刘宝琛和邹金峰等人的研究，单元体单位引起的地表沉降表达式为

    式中：r(z)为地表下沉主要影响半径.

    线性叠加每个单元体开挖在地表同一点引起的沉降，即可计算出隧道开挖引起倾斜地表任一点的沉降.

2.   三维倾斜地表沉降计算

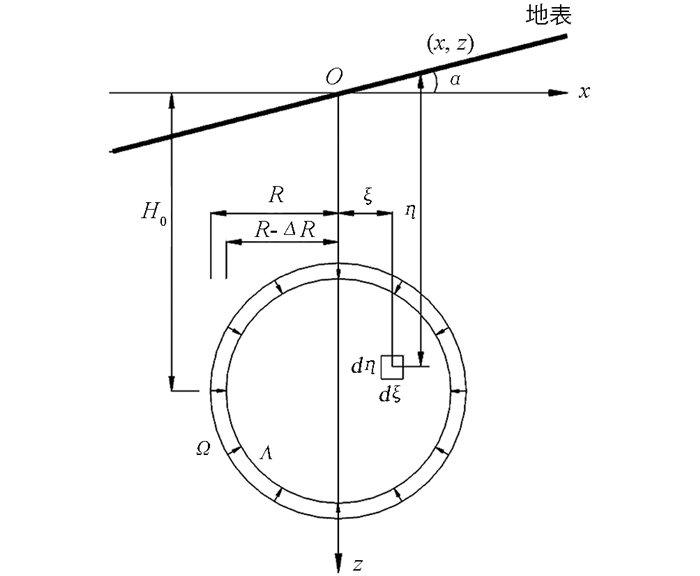
  • 将倾斜地表沿x方向和y方向分解，沿x方向倾斜角度为α，沿y方向倾斜角度为θ，对于一般情况，隧道可以近似看成很长的柱形体，它的开挖横截面不沿长度变化.由于隧道开挖是平面问题，因此在每个平面开挖时，位移分量不沿y方向变化，而只是x和z的函数.倾斜地面下，单孔隧道开挖引起的三维地表沉降计算可分解为无数个单个平面开挖引起的沉降计算.开挖隧道半径为R，平均收敛为ΔR，过开挖横截面中心点取竖直向下为z轴建立直角坐标系，地表倾角为α，H0为横截面圆心到x轴的距离，取开挖单元dx dz，η和ξ分别为开挖单元体至地表和z轴的距离，则由该单元开挖引起的位移由以上分析可计算，计算简图如图 3所示.

    横截面中坐标为(x，z)的点在dx dz单元体开挖的情况下，地表沉降为

    根据刘宝琛等人的研究(1993)，影响半径r(η)可用土体主要影响角β和内摩擦角φ表示为

    土体主要影响角用内摩擦角表示：

    隧道开挖后及时支护，隧道收缩引起的地表沉降，根据随机介质理论原理及其假定，隧道开挖引起的地表沉降量应为初始开挖断面Ω与收缩后断面Λ引起的地表沉降之差，隧道初始开挖断面Ω半径为R，隧道收缩后断面Λ半径为R-ΔR.

    则横截面中横坐标为x的任意一点距地表高度为

    对式(4)进行积分，横截面中地表任一点二维平面下隧道开挖引起的地表沉降可表示为

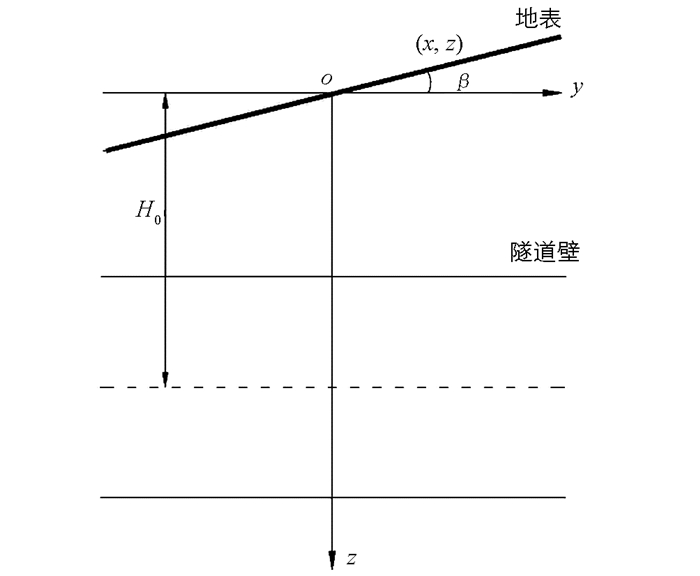
    对于倾斜地表，在y方向也存在一定倾角，即三维空间中开挖单元据地表距离随y轴变化，倾斜角度为θ，如图 4所示.则地表坐标为(x，y，z)点距隧道中心轴线高度：

    倾斜地表下隧道开挖后，圆形隧道半径R均匀径向收缩后为R-ΔR，地表上任意一点(x，y，z)沉降为

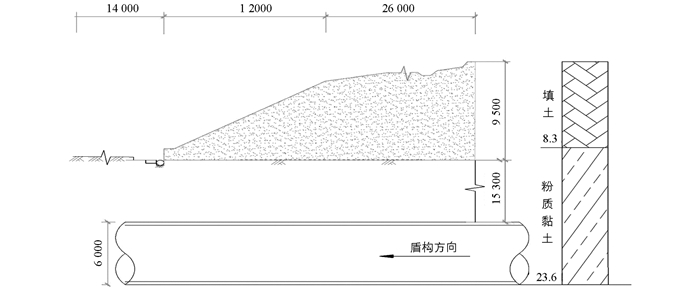
    长沙地铁一号线下穿京广铁路线及其周边边坡，开挖隧道上方土体以填土和粉质黏土为主.盾构开挖隧道直径为6 m，边坡距隧道顶端最近和最远距离分别为15.3 m和24.8 m，垂直隧道开挖方向地表倾角α=4.8°.根据监测资料，开挖断面收缩稳定后，计算范围内隧道平均径向收敛量为12.2 cm.由现场实验测试结果可知，隧道上方土体内摩擦角φ=25°.沿隧道盾构方向，开挖隧道与边坡断面如图 5.

    取倾斜地表投影水平面为30 m×30 m的范围进行计算，计算范围内最高点坐标为(30，30，z)，到隧道中心线垂直距离为24.8 m，为方便计算，将斜坡视作为均匀倾斜，沿隧道开挖方向斜坡倾角为

    则，

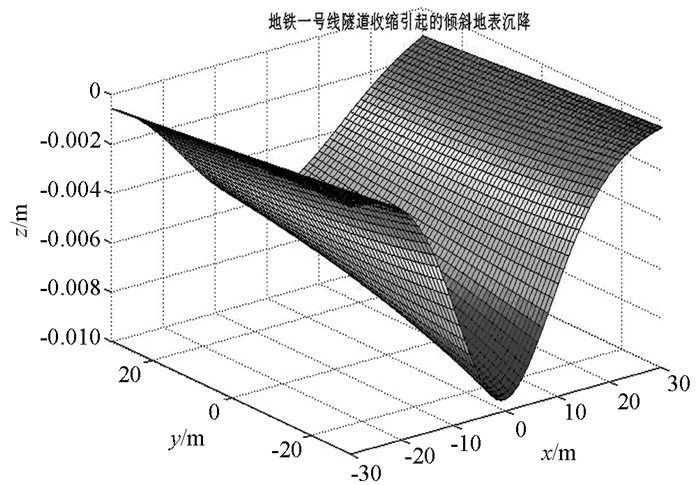
    使用MATLAB编程计算得到斜面沉降值如图 6所示.从地铁一号线开挖阶段实时监测日报中筛选地表沉降稳定后的监测数据，随机选取其中6个观测点与理论计算结果进行对比验证.

    根据工程测量报告中随机选取的6个观测点的稳定沉降数据和相对应点使用本文计算方法得出的数据对比和误差分析可以得出，理论计算结果和沉降测量值基本接近，只有第2和第5个点误差偏大，大于10%.根据文献[20]的研究和计算模型分析，造成该误差原因可能有4点：①监测点位置的岩土体进行了加固，导致监测点实际沉降偏小，②附近存在桩基阻止了地表沉降，③计算模型相对实际情况进行了简化，计算高度与实际高度存在一定误差，④由于客观因素导致监测数据存在一定的误差.综上所述，6组倾斜地表实测值和理论值吻合度较高，平均误差仅为5.92%.

3.   算例与参数分析

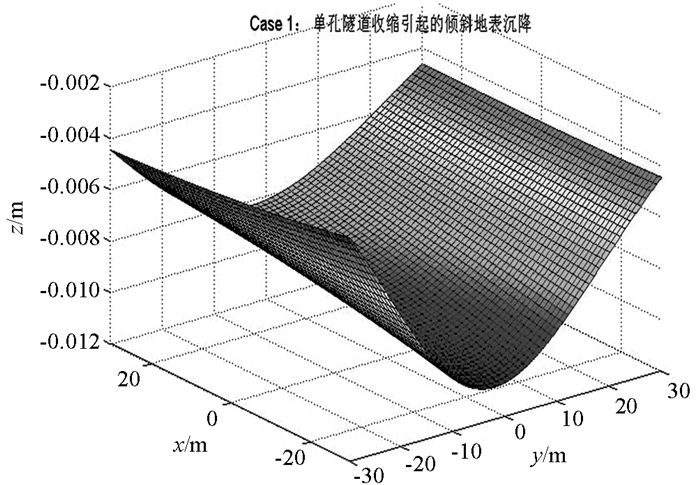
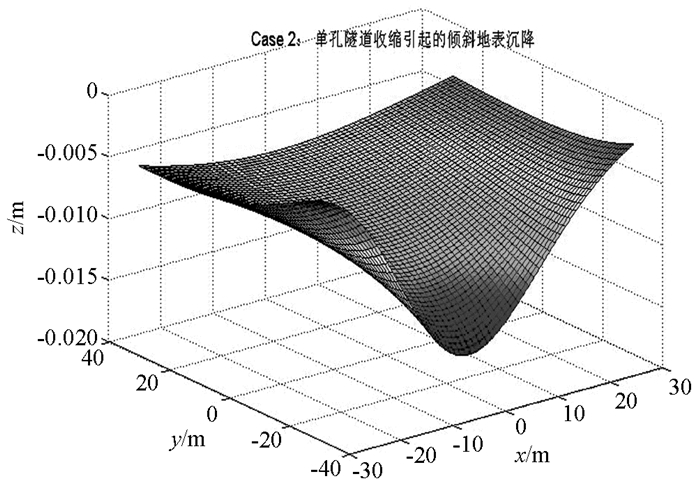
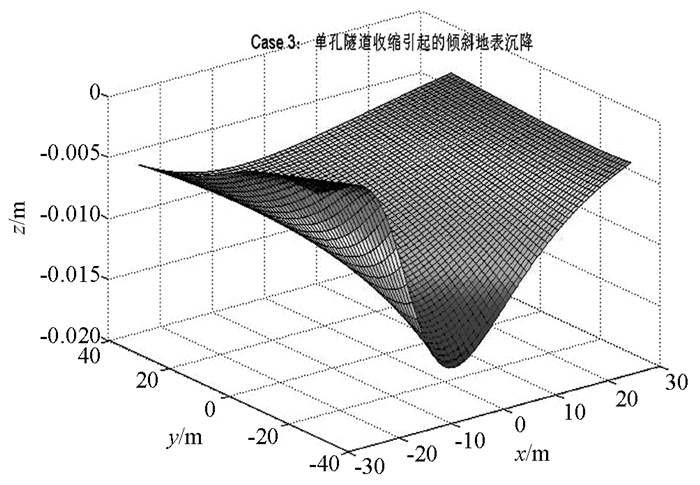
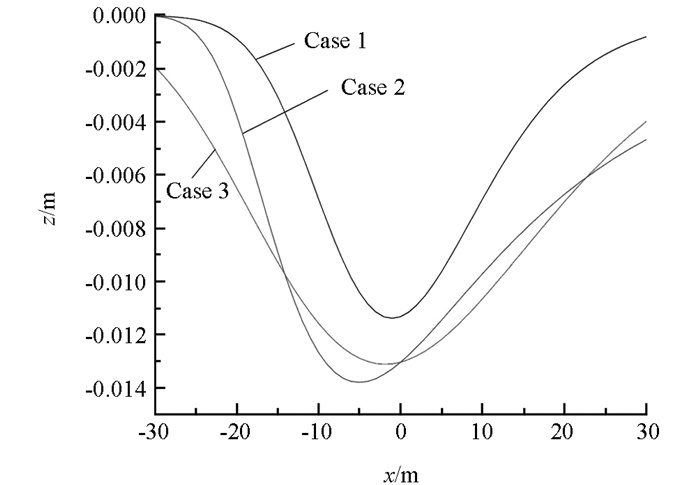
  • 大多数学者对于地表沉降相关研究均基于水平地表，然而地表倾斜对于地表产生不均匀沉降的影响也不可忽略，尤其是对于地铁隧道等埋深较浅的隧道，为研究地表倾斜度对地表不均匀沉降的影响，取文献[18]中工程实例参数进行分析，其中：隧道半径R=3 m，径向收敛量ΔR=0.031 m，H0=40 m，φ=25°.计算范围取倾斜地表投影水平面为30 m×30 m，分别计算倾斜角α=10°，θ=10°；α=10°，θ=30°；α=30°，θ=30°三种情况下的地表沉降，如图 7-图 9所示，并选取y=-20 m处的沉降进行对比.

    从图 7-图 9中可以明显地看出，隧道中心线处对应的地表沉降量较大，距离开挖隧道越远，地表沉降量越小. 图 7与图 8，图 8与图 9分别对比可知，地表倾角越大，地表不均匀沉降越明显.

    Case1和Case2中沿x轴方向倾角相同，沿y方向倾角不相同，在y=20 m处，坐标相同的计算点Case 2中距隧道的距离比Case 1小，图 10可以看出Case 2中沉降大于Case 1中的沉降，表明随着地表距开挖单元越近，沉降越大，即地表沉降随着隧道埋深减小而增大. Case1和Case3中沿x轴方向倾角等于沿y方向倾角相同，而Case2不同，图 8中沉降数据表明，相同倾角的情况下，沉降最大点与x=0 m处更接近.

4.   小结

  • 本文针对大多数隧道开挖工程处于倾斜地表下的情况，建立了倾斜地表下隧道开挖模型.基于随机介质理论原理中隧道开挖过程可分解为无数个微小单元体开挖的特性，建立单元体开挖计算模型，将隧道开挖位移求解简化为平面问题，基于随机介质理论推导了三维倾斜地表沉降计算方法，并结合长沙地铁一号线工程实例验证了计算方法的可靠性，根据选取的6个监测点对比得到综合误差为5.92%，并且从岩土体加固、基础建筑设施、模型简化和观测误差4个方面对比分析了可能产生误差的原因.最后对地表倾斜度进行参数分析，结论表明地表斜面倾角越大，地表不均匀沉降越明显，开挖隧道越深，地表沉降越小.

Figure (10)  Table (1) Reference (18)

Catalog

    Copyright Journal of Southwest University Natural Science Edition

    Address： Tel：023-68254576, 68252540, 68366165,68366917 E-mail：lkxb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return