Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2020 Volume 42 Issue 6
Article Contents
Previous Article Next Article

Ya-xun YANG, Wen-hao CHAI, Fu-li YANG, et al. Study on Optimal Layout of Strain Sensors for Continuous Rigid Frame Bridges Based on Full-Life Cycle[J]. Journal of Southwest University Natural Science Edition, 2020, 42(6): 119-127. doi: 10.13718/j.cnki.xdzk.2020.06.014
Citation: Ya-xun YANG, Wen-hao CHAI, Fu-li YANG, et al. Study on Optimal Layout of Strain Sensors for Continuous Rigid Frame Bridges Based on Full-Life Cycle[J]. Journal of Southwest University Natural Science Edition, 2020, 42(6): 119-127. doi: 10.13718/j.cnki.xdzk.2020.06.014
shu

Study on Optimal Layout of Strain Sensors for Continuous Rigid Frame Bridges Based on Full-Life Cycle

  • School of Highway, Chang'an University, Xi'an 710064, China

More Information
  • Received Date: 18/02/2020
    Available Online: 01/06/2020

  • MSC: U447

  • Aiming at the problems of the independent arrangement of strain sensors of continuous rigid frame bridges in the construction and operation stages, we used shell elements instead of traditional beam elements to establish a finite element model of continuous rigid frame bridges. We improved the traditional genetic algorithm, using matching fitness and the key section method, and proposed a sensor optimization method for continuous rigid frame bridges with a full life cycle. Taking a four-span continuous rigid-frame bridge as an example of the optimal layout, the strain sensor optimization method proposed in this paper was used to optimize the layout of the strain sensors of the bridge, and the strain modal criterion was used as the evaluation criterion to compare it with other traditional methods. The results showed that the method described in this paper was superior to other methods and could be used as a strain sensor layout method for continuous rigid frame bridges in full life cycle.
  • 加载中
  • [1] 韩亮, 樊健生.近年国内桥梁垮塌事故分析及思考[J].公路, 2013, 58(3):124-127.

    Google Scholar

    [2] ZHU S, LEVINSON D, LIU H X, et al. The Traffic and Behavioral Effects of the I-35W Mississippi River Bridge Collapse[J]. Transportation Research Part A:Policy and Practice, 2010, 44(10):771-784. doi: 10.1016/j.tra.2010.07.001

    CrossRef Google Scholar

    [3] 刘斐.近期桥梁安全事故深度调查与分析[D].长沙: 中南大学, 2014.http://cdmd.cnki.com.cn/Article/CDMD-10533-1014407042.htm

    Google Scholar

    [4] 梁鹏, 李斌, 王晓光, 等.基于桥梁健康监测的传感器优化布置研究现状与发展趋势[J].建筑科学与工程学报, 2014, 31(1):120-129. doi: 10.3969/j.issn.1673-2049.2014.01.015

    CrossRef Google Scholar

    [5] 吴子燕, 代凤娟, 宋静, 等.损伤检测中的传感器优化布置方法研究[J].西北工业大学学报, 2007, 25(4):503-507. doi: 10.3969/j.issn.1000-2758.2007.04.008

    CrossRef Google Scholar

    [6] 刘艳, 刘贵杰, 刘波.传感器优化布置研究现状与展望[J].传感器与微系统, 2010, 29(11):4-6, 13. doi: 10.3969/j.issn.1000-9787.2010.11.002

    CrossRef Google Scholar

    [7] KAMMER D C, TINKER M L. Optimal Placement of Triaxial Accelerometers for Modal Vibration Tests[J]. Mechanical Systems and Signal Processing, 2004, 18(1):29-41.

    Google Scholar

    [8] 詹杰子, 余岭.传感器优化布置的有效独立-改进模态应变能方法[J].振动与冲击, 2017, 36(1):82-87.

    Google Scholar

    [9] 杨雅勋, 郝宪武, 孙磊.基于能量系数-有效独立法的桥梁结构传感器优化布置[J].振动与冲击, 2010, 29(11):119-123, 134, 257. doi: 10.3969/j.issn.1000-3835.2010.11.026

    CrossRef Google Scholar

    [10] 杨志魁.基于灵敏度有效独立的传感器优化布置研究[D].西安: 长安大学, 2013.http://cdmd.cnki.com.cn/Article/CDMD-10710-1014022445.htm

    Google Scholar

    [11] LIA D S, LI H N, FRITZEN C P. The Connection Between Effective Independence and Modal Kinetic Energy Methods for Sensor Placement[J]. Journal of Sound and Vibration, 2007, 305(4-5), 945-955. doi: 10.1016/j.jsv.2007.05.004

    CrossRef Google Scholar

    [12] YI T H, LI H N, ZHANG X D. Health Monitoring Sensor Placement Optimization for Canton Tower Using Immune Monkey Algorithm[J]. Structural Control & Health Monitoring, 2015, 22(1):123-138.

    Google Scholar

    [13] 殷红, 杜国璋, 彭珍瑞, 等.野草猴群算法的传感器优化布置方法研究[J].计算机工程与科学, 2018, 40(4):626-635. doi: 10.3969/j.issn.1007-130X.2018.04.008

    CrossRef Google Scholar

    [14] 杨振伟, 周广东, 伊廷华, 等.基于分级免疫萤火虫算法的桥梁振动传感器优化布置研究[J].工程力学, 2019, 36(3):63-70.

    Google Scholar

    [15] 马小晋, 许华虎, 卞敏捷, 等.基于改进模拟退火算法的虚拟机调度优化方法[J].通信学报, 2018, 39(S1):278-287.

    Google Scholar

    [16] 罗娜.改进的模拟退火算法及其在装填问题中的应用[J].电脑知识与技术, 2016, 12(6):181-183.

    Google Scholar

    [17] 朱豪, 彭艺, 张申, 等.基于改进遗传算法的自适应越区切换方案[J].吉林大学学报(理学版), 2020, 58(1):133-139.

    Google Scholar

    [18] ZHANG Y, LIU M. An Improved Genetic Algorithm Encoded by Adaptive Degressive Ary Number[J]. Soft Computing, 2018, 22(20):6861-6875. doi: 10.1007/s00500-017-2981-0

    CrossRef Google Scholar

    [19] 曹孟华, 李龙, 谢红卫.改进遗传算法在传声器阵列优化中的应用[J].国防科技大学学报, 2019, 41(6):126-134.

    Google Scholar

    [20] 刘宇, 毕丹, 李兆霞.大跨斜拉桥基于遗传算法的传感器优化布置方法[J].东南大学学报(自然科学版), 2009, 39(4):825-829. doi: 10.3969/j.issn.1001-0505.2009.04.034

    CrossRef Google Scholar

    [21] 高大威, 陈海峰, 李翠, 等.扭力梁后桥剪切中心对悬架性能的影响[J].重庆理工大学学报(自然科学版), 2018, 32(10):17-26. doi: 10.3969/j.issn.1674-8425(z).2018.10.002

    CrossRef Google Scholar

    [22] 陈栋, 葛玉梅.波形钢腹板桥加速度多点激励随机振动分析[J].重庆理工大学学报(自然科学版), 2018, 32(5):115-118. doi: 10.3969/j.issn.1674-8425(z).2018.05.018

    CrossRef Google Scholar

    [23] ZHANG J, MAES K, ROECK G D, et al. Optimal Sensor Placement for Multi-Setup Modal Analysis of Structures[J]. Journal of Sound and Vibration, 2017, 401:214-232. doi: 10.1016/j.jsv.2017.04.041

    CrossRef Google Scholar

    [24] 李建国, 张海飞, 周璐婕, 等.基于改进遗传算法的立体车库布局对比及服务资源优化[J].西南大学学报(自然科学版), 2019, 41(4):139-148.

    Google Scholar

    [25] 周磊, 张力文, 周建庭.基于二重结构编码遗传算法的连续刚构桥传感器优化布置[J].公路, 2014, 59(11):36-41.

    Google Scholar

    [26] 窦金梅.基于遗传算法的钢桥单元制造车间生产优化调度[D].上海: 上海交通大学, 2013.http://cdmd.cnki.com.cn/Article/CDMD-10248-1014008504.htm

    Google Scholar

    [27] 范玉, 吴雪峰, 王耿, 等.基于遗传算法的复摆式破碎机动颚运动特性优化[J].西南大学学报(自然科学版), 2018, 40(2):174-178.

    Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(10)  /  Tables(3)

Export Citation
PDF
XML

Article Metrics

Article views(2922) PDF downloads(226) Cited by(0)

Access History

Other Articles By Authors

Study on Optimal Layout of Strain Sensors for Continuous Rigid Frame Bridges Based on Full-Life Cycle

  • Received Date: 18/02/2020
  • Available Online: 01/06/2020

Abstract: Aiming at the problems of the independent arrangement of strain sensors of continuous rigid frame bridges in the construction and operation stages, we used shell elements instead of traditional beam elements to establish a finite element model of continuous rigid frame bridges. We improved the traditional genetic algorithm, using matching fitness and the key section method, and proposed a sensor optimization method for continuous rigid frame bridges with a full life cycle. Taking a four-span continuous rigid-frame bridge as an example of the optimal layout, the strain sensor optimization method proposed in this paper was used to optimize the layout of the strain sensors of the bridge, and the strain modal criterion was used as the evaluation criterion to compare it with other traditional methods. The results showed that the method described in this paper was superior to other methods and could be used as a strain sensor layout method for continuous rigid frame bridges in full life cycle.

    HTML

  • 近年来，桥梁建设和运营阶段中出现的事故不断发生，例如：辽宁抚顺市月牙岛西桥与美国密西西比河I-35W钢桁架拱桥垮塌[1-2].针对此类事件的频繁发生，桥梁监测被广泛应用到桥梁建设与后期运营阶段，而传感器的优化布置则是桥梁监测的基础.通常来说，桥梁监测中的传感器布置越多，则获取的桥梁结构数据会越多，能更全面地反映桥梁结构的实际状态.但是使用过多的传感器会导致桥梁运营阶段的监测成本增大，所以将传感器布满桥梁结构的所有可能测点既不合理又不经济[3].因此，如何采用更少的传感器得到更多的桥梁结构信息，即传感器优化布置问题成为了桥梁结构监测中的一个关键型问题.

    在传感器的优化布置方面，主要有：有效独立法、灵敏度系数法、运动能量法、遗传算法(GA)、猴群算法、萤火虫算法、模拟退火算法等优化布置方法[4-6]，针对这些方法，国内外学者做了大量研究. Kammer等人提出了有效独立法，该方法是选择结构目标模态矩阵中独立性贡献最大的节点进行布置[7].詹杰子、杨雅勋、杨志魁等人对于传统的有效独立法做出了一定的改进，并验证了方法的有效性[8-10]. LIA等人讨论了有效独立法和运动能量法之间的内在联系，认为前者可以通过对后者迭代得到[11]. YI、殷红等人分别改进了猴群优化算法，并验证了优化方法的有效性[12-13].杨振伟等人将等级划分策略和免疫机制引入萤火虫算法中，提出了基于分级免疫萤火虫算法[14].马小晋、罗娜等人对模拟退火算法进行了改进，并验证了其优化方法的有效性[15-16].朱豪、Zhang Y、曹孟华等人分别对遗传算法做出了一定的改进，并通过实例验证了其方法的有效性[17-19].刘宇等人采用遗传算法对优化算法评价指标做了分析对比，指出了MAC矩阵是最有效的评价指标[20].但是，目前大多数都是对传感器的优化方法进行了改进，且将优化方法直接用于桥梁建设或运营阶段监测中，并没有考虑到桥梁建设—运营阶段的监测相互结合，造成了两阶段数据不必要的浪费[21-22].

    本文针对连续刚构桥全寿命周期内各阶段独立进行监测的现状，基于改进的遗传算法，对连续刚构桥全寿命周期内的应变传感器的优化进行了研究，提出了基于匹配适应度的全寿命传感器优化布置方法，并以某四跨连续刚构桥为实例进行应变传感器的优化布置，最后通过应变模态保证准则评价本文算法的有效性.

1.   理论基础

    1.1.   应变模态保证准则(SMAC)

  • 目前传感器的优化布置准则多是以位移模态作为其优化目标，这种优化布置准则对于加速度与位移传感器的测点优化布置非常适用，但对于应变传感器的优化布置适用性不高.而对于连续刚构桥全寿命周期监测的应变传感器，若采用传统方式，则会导致优化效率不高，故在传统的模态保证准则(MAC)的基础之上，采用应变模态作为优化目标，采用应变模态保证准则作为应变传感器优化布置准则.由于应变模态同位移模态一样，也具有正交特性，借鉴于模态保证准则的定义，应变模态保证准则可以表示为

    上式中：SMAC(i，j)表示应变模态向量，φiT、φjT分别表示矩阵φi、φj的转置矩阵，右下角标i、j分别表示第i、j阶模态行向量.

    两模态向量之间的相关性可以通过对应的SMAC矩阵中的非对角元素SMAC(i，j)的值来判断.当SMAC(i，j)(i≠j)的取值为1，表示两向量的夹角为0，无法区分两个模态；当取值为0，表示两模态向量相互正交；当两模态向量可以很容易分辨，一般认为大于0.9时，意味着两个模态相关，两个向量不可分辨；小于0.25时，则可认为两个模态相互正交，可以很好分辨[23].

    • 1.2.   遗传算法

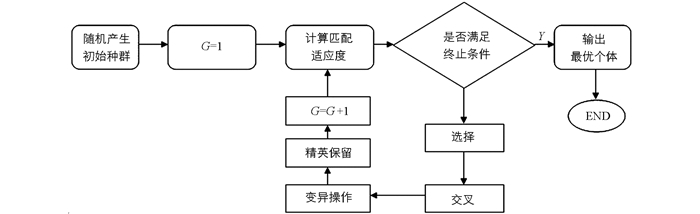
  • 遗传算法模拟了达尔文生物进化论的自然选择和遗传学机理的生物进化过程，是一种模拟自然进化过程的仿生算法.遗传算法主要包括5个基本部分：参数编码、初始种群选择、适应度函数选取、遗传操作的选择和控制参数的选取[24-27].

    参数编码：选择二进制编码作为本文的参数编码方式，二重编码结构图见表 1.每个个体的二重编码由附加码和变量码两部分构成，附加码中的m(i)表示应变传感器的布置测点，变量码中的Xm(i)表示附加码m(i)的取值(当取值为1，表示该位置布置应变传感器；当取值为0，则表示不布置应变传感器). n为实际情况中所有可能的测试断面数或者测点数目.

    对于个体编码，首先采用洗牌的方式产生附加码{m(i)，(i=1，2，…，n)}，然后采用随机数的方式产生对应的变量码值(0或1)，两者相互形成个体的二重编码.例如：对有8个节点的个体随机生成附加码：7，2，6，1，4，8，5，3，相应的变量码为：0，1，1，0，0，1，0，0，则表示节点号为2，6，8的节点布有传感器.

    在产生初试个体之后，通过选择、交叉、变异等操作来进行产生下一代.其中交叉算子和变异算子以及选择操作是影响遗传算法中的主要因素，本文主要通过部分匹配交叉PMX(partially matched crossover)和逆位遗传算子来完成选择操作.

    适应度函数选取：遗传算法的适应度函数是用来判断群体中的个体的优劣程度的指标，它是对个体是否适应该问题进行判断，并作为以后遗传操作的依据.本文是以应变模态保证准则的非对角元素最小化来进行应变传感器的优化布置，但遗传算法却是以适应度最大化作为其问题的优化指标，故需要将优化准则函数转化为合适的遗传算法的适应度函数，如式(2).

    式中：f(x)=max{SMACij}

    • 1.3.   匹配适应度

  • 为了让建设阶段和运营阶段之间的传感器更好地结合起来，提出了两者匹配适应度的概念.由于建设过程的传感器已经确定，而运营期内的传感器则可以考虑对已有的传感器进行匹配，全寿命传感器优化布设的目的是让两阶段的传感器协同工作，使得监测数据更好地被利用.在遗传算法中进行适应度计算时，传统的算法只会考虑前N阶模态矩阵M.假设测点自由度有5个(2，3，6，9，10)被选中，传统的适应度会根据M1来计算，而本文的匹配适应度则会考虑两阶段传感器的自由度.假设预埋传感器自由度编号为13与15被选中，根据M2矩阵计算匹配适应度.

    式中：ε代表应变模态，上标数字代表测点自由度，下标代表模态阶数.

    • 1.4.   关键截面法

  • 采用位移模态保证准则来对传感器进行优化布置时，有限元模型一般采用梁单元来模拟，因为梁单元的一个节点对应于一个监测截面，该截面拥有唯一位移值，既满足了位移要求又减少了建模工作量.但对于应变而言，一个监测截面之上有多个应变测点，若采用梁单元模型来获取该截面的应变数据，将会导致该截面的应变数据很难反映出应变测点的空间分布规律，会给应变传感器的优化布置带来一定误差.故本文建立模型时采用壳单元建立三维空间模型，更好地反映截面的应变模态.在连续刚构桥优化布置中，直接从所有的壳单元测点开始，利用遗传算法去寻找最优测点进行布置显然是不合适的，因为得到的最优测点的位置往往是没有任何顺序且相对分散.对某连续梁采用本文方法进行优化选择测点(30个)，图 1是一次运行结果，可以看出，优化测点不会集中在某几个截面，若按照这种方式布置，在后期的数据管理与处理过程中，显然是不合适的.为此，提出了关键截面法的概念，关键截面法的思路是首先在截面上确定最优测点布设方式，形成标准截面，之后让这几个测点的应变模态数据代表该截面参与后期的优化计算，确定最后的布置截面.以此来确定最优测点.

2.   全寿命周期传感器综合优化方法

  • 对连续刚构桥而言，目前很多桥梁都把桥梁的建设阶段、后期运营阶段的监测分开独立进行，未能将其结合在一起.造成数据和传感器资源的浪费，本文将这两阶段进行优化.目前，在建设过程中，一般选择箱梁根部、L/4、L/2等关键截面为最不利的控制截面，进行传感器布置.该截面的选择已经成熟，更为重要的是选择运营阶段的截面，从而使得施工监控布置的传感器与运营期即将布设的传感器在运营中可以达到最优化.本文提出了两阶段匹配适应度的概念，通过遗传算法的迭代使得建设阶段与运营阶段的应变传感器的匹配适应度达到最优，其优化示意图见图 2.在优化过程中，采用应变模态保证准则作为优化准则，最终选择出合适的截面进行运营阶段的应变传感器布置.

3.   工程实例

    3.1.   工程背景

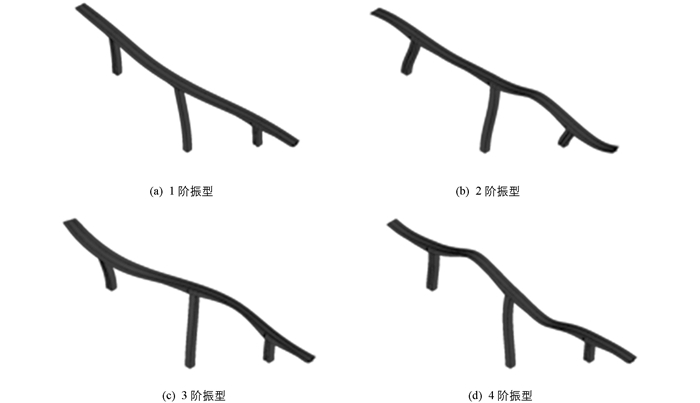
  • 以某四跨预应力混凝土变截面连续刚构桥为例，其跨径组合为(75+2×140+75)m，截面类型为单箱单室，下部结构为薄壁空心墩，混凝土等级为C50，采用大型通用有限元软件ANSYS建立其有限元模型，为精确模拟桥梁结构，采用shell163单元来对箱梁进行精细化模拟，其中顶板、腹板和底板的变厚度通过Rthick命令实现.全桥共36 976个节点，36 792个单元，全桥的有限模型如图 3所示，计算其动力特性，获得前20阶自振频率及固有振型(表 2)，前4阶振型如图 4.通过分析该桥的自振特性，考虑到应变测试方向为顺桥方向，选择竖向模态的前5阶作为优化目标，从表 2可以看出，前5阶竖向模态分别为第4，6，10，11，13阶模态.

    • 3.2.   优化布置方案

  • 建设过程中，根据经验选择了中、边跨箱梁的根部、L/4、L/2等共16个截面作为建设阶段应变传感器布置截面.每个监测截面布设6个应变测点，则全桥一共布设了96个预埋应变测点.根据建立的模态置信矩阵计算预埋传感器的SMACym矩阵，并将其绘制为柱形图，其结果见图 5.从图 5可以看出，SMACym矩阵中的非对角元素部分值大于0.25.最大值为0.309 1，不符合文献[21]中的建议数值.所以在运营阶段应变传感器布置时，采用本文提出的优化方法对加入运营期的表贴传感器进行优化布置.

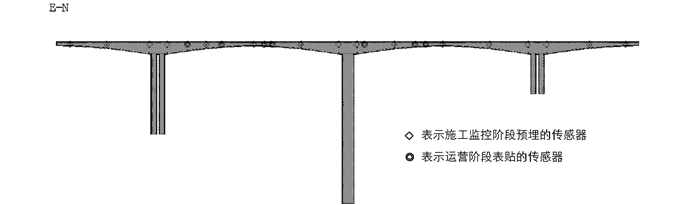
    全桥所有可能的表贴测点(运营阶段传感器布置测点)则有2 622个，利用关键截面的思想，先在每个测试截面内利用改进的遗传算法找到6个最优目标布置点，形成一个标准测试断面，标准截面测点示意图如图 6所示，然后联合施工阶段布置应变传感器的测点，获取所有测点的模态数据.在ANSYS模型中排除以下3类截面，(1)施工阶段预埋的测试截面；(2)无法布置传感器的截面；(3)离约束条件较近的截面，总共有405个可能测试截面，本文只选择7个关键截面作为最终表贴截面，这7个截面与原本的预埋传感器的截面的匹配适应度达到最大，得到截面编号之后，根据映射关系找到对应的测点.其最终截面编号和测点编号见表 3，全桥最终应变传感器的布置方案如图 7所示.

    • 3.3.   方法评价

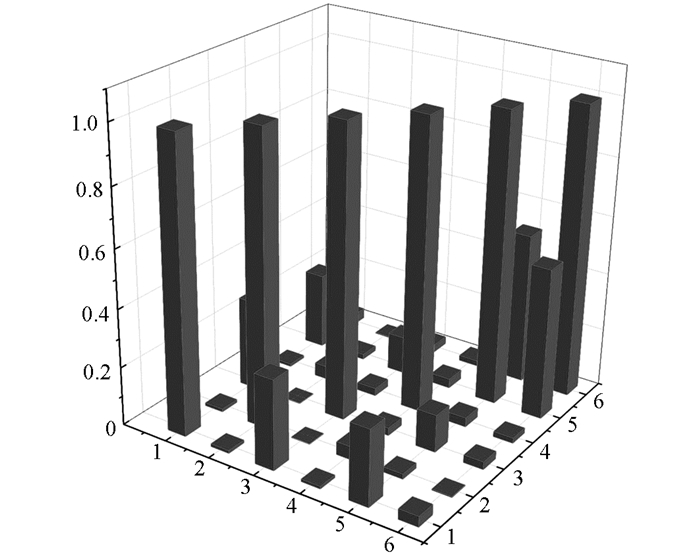
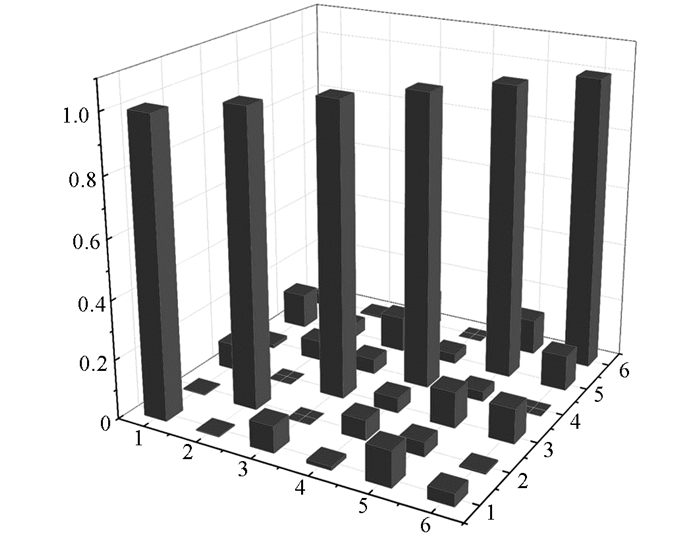
  • 采用应变模态保证准则作为评价准则，按本文方法，计算优化后(预埋—表贴)应变的模态置信度矩阵SMACPP柱状图见图 8.

    从图 8中可以看出，最终两阶段应变传感器的SMACPP矩阵中最大非对角元素的值为0.120 6，远小于建议数值.这表明预埋的应变传感器和运营阶段的表贴应变传感器之间的模态向量有很好的正交性.且可以很好地分辨出来，说明本文提出的全寿命阶段应变传感器布设方法可行.

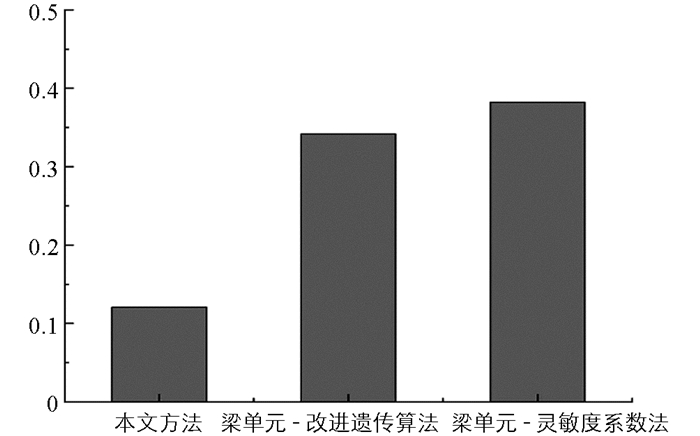
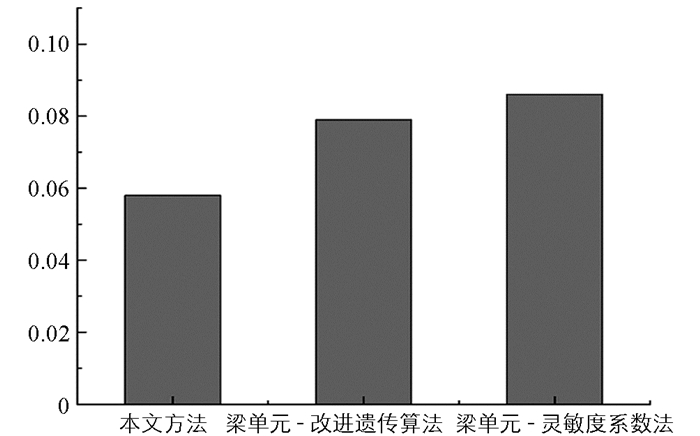
    为了更好说明本文方法优点，采用以下两种方法进行对比：(1)采用传统的测点布设进行对比，采用梁单元(Beam189)建立有限元模型并采用本文提出的改进遗传算法进行应变传感器优化布置；(2)采用梁单元建模，利用灵敏度系数法去进行应变传感器优化布置.计算上述两种方法的SMAC矩阵，进行非对角线最大值和平均值比较.

    从图 9和图 10中，针对3种不同尺度建模、不同算法传感器的优化方案，在应变模态保证准则下，本文中的非对角线元素最大值为0.120 8，均值为0.058，梁单元—改进遗传算法的非对角线元素最大值为0.341 6，均值为0.079，梁单元—灵敏度系数法的非对角线元素最大值为0.382 2，均值为0.086.这说明本文方法优于其他两种方法，且说明应变传感器对于建模深度有一定要求，采用梁单元模型会在一定程度上影响应变传感器的优化布置效果；另一方面，说明本文方法考虑了运营阶段的应变传感器，满足了优化布置.

4.   结论

  • 本文针对连续刚构桥中应变传感器在建设阶段和运营阶段独立布置现状，改进了传统的遗传算法，提出了适用于全寿命周期的连续刚构桥的传感器优化方法，并通过实例验证，得到以下结论：

    1) 针对于多跨连续刚构桥，分别建立了梁单元和壳单元模型进行应变传感器布置，对比分析得出采用壳单元建立精细化的有限元模型更能反映桥梁的空间动力特性，更利于应变传感器优化布置；

    2) 对传统的遗传算法进行了改进，提出了一种基于匹配适应度的全寿命优化方法.经过实例验证，该方法可以有效地将建设阶段与运营阶段的应变传感器进行优化结合，提高应变传感器布置的有效性与经济性；

    3) 通过3种不同优化方法，采用应变模态准则作为评价准则，对比说明本文提出的方法优于其他方法，可作为连续刚构桥应变传感器的布置方法.

Figure (10)  Table (3) Reference (27)

Catalog

    Copyright Journal of Southwest University Natural Science Edition

    Address： Tel：023-68254576, 68252540, 68366165,68366917 E-mail：lkxb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return