Optimal Portfolio Selection Considering Deposit and Loan Spreads and Transaction Costs

假设投资者投资于无风险资产，如银行存款，则存入银行的本金价格满足方程

r(t)表示存款利率，R(t)表示贷款利率并且R(t)＞r(t).投资于风险资产(股票)的价格S(t)服从经典的Merton模型

其中b(t)表示股票的预期收益率，σ(t)表示波动率.考虑一个概率空间(Ω，ξ，P，ξ_t)，这里的B_t是概率空间上的一维Brown运动. ξ_t，0≤t≤T，是由此布朗运动生成的域流，满足

我们定义π(t)为投资于股票的金额，C(t)为单位时间的消费量，W(t)为总的财富.假设

此外，针对我国银行政策制度的规定：商业银行及相关专业银行不得发放贷款给个人用于投资股票等风险性投资，因此越来越多的投资者选择向支付宝网商银行、微粒贷或非银行金融机构等借贷方式进行借贷投资.据Wind数据库显示，小额信贷公司在2010，2011，2012这3年用于个人中长期贷款的金额分别为12.58，43.56，85.58亿元，其中用于股权及其他投资的金额分别为6.01，8.74，31.69亿元，呈明显上升趋势.本文中，假设投资者可以通过向非银行金融机构，比如小额信贷公司进行贷款投资.

假设股票市场存在交易费，当投资者买入或卖空股票时都需要按照固定的比率交纳交易费，买入和卖空交易费率相同，设为k∈[0，1).并且还假定所有市场系数在t∈[0，T]上都是确定的且有界.

π(t)可正、可负、可为零，当π(t)＜0时表示投资者卖空持有的股票，π(t)＞0表示买入股票，π(t)=0表示投资者把所有资金存入银行.同样，存入银行账户的资金W(t)-π(t)也可正、可负，W(t)-π(t)＞0表示投资者向银行账户存款，W(t)-π(t)＜0表示投资者需要向小额信贷公司贷款.消费C(t)不得低于0.

定义(允许组合策略)  如果投资者在t时刻的消费和投资策略(C_t，π_t)满足W_t≥0，称此策略为允许组合策略(即投资者要有一定的偿付能力，不能恶意透支).记允许组合策略全体为

本文的目的就是找出消费—投资策略组合，使效用达到最大化，则投资者的财富过程满足以下随机微分方程

其中w≥0是初始财富.

令

其中，j(C，·)被假定为严格凹的效用函数，也就是j^′(C，·)＞0，j^″(C，·)＜0，h(W(T)，T)是特定的“遗赠评价函数”(在生产增长模型中，称为“残值函数”)，通常假定它是W(T)的凹函数. t∈[0，T]，E为W(0)=w的条件期望算子. j和h关于C和W都是可微的.投资者的目标就是选择最优的消费—投资组合，使得从消费及最终财富中获得最大效用.因此，建立最优消费—投资策略选择模型为

根据动态规划原理及Ito's引理，公式(5)对应的HJB方程为

其中V_w，V_ww和V_t分别表示值函数V关于相应变量的一阶导和二阶导.设(C^*，π^*)是最优的消费—投资策略.那么，公式(6)左边对C求一阶导数可得

引理1  若j(C，·)，h(C，·)分别是关于C，W的凹函数，则值函数V(W，t)也是单调递增的凹函数.

证  根据公式(4)，定义

J(W(T)，T)=h(W(T)，T)是约束条件，由上式有

如果t≡t₀+Δt，Δt是两期之间的时间间隔，并且J(W(t₀)，t₀)的三阶偏导数存在，那么根据泰勒定理和积分中值定理，可以把公式(8)重新写为

其中t∈[t₀，t]，公式(9)中每一项都取期望，等式两边同时减去J(W(t₀)，t₀)，然后将方程两边同除以Δt，对所得方程令Δt→0取极限，则公式(9)变为Bellman-Dreyfus基本最优方程为

令

则其正则内部最大值的一阶条件是

而正则内部最大值的充分条件为β_ππ＜0，又根据公式(5)及j^′(C)＞0，因此得证.

我们知道当投资者选择投资一种股票时不能同时买入和卖出，因此本文分两种情形分别讨论，即π(t)≥0和π(t)＜0.另外，投资者在面对股市的牛、熊市时，会分别买入和卖空股票；当贷款利率过高时，贷款成本较高，这会导致投资者将现有资金投入股市，不会选择贷款；当存款利率较高时，相反会促使投资者将更多资金甚至卖空股票所得的资本利得存入银行.因此，市场状态的优良对投资者做出什么样的决策至关重要.本文分投资者买入和卖空两种情形来分析.

情形1  π(t)≥0

公式(6)式可写为

定义

显然

则根据公式(12)解

同样根据公式(13)解

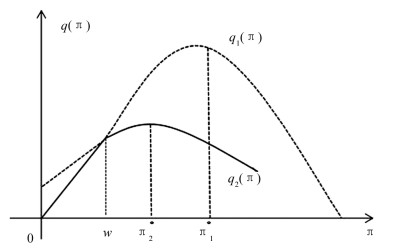
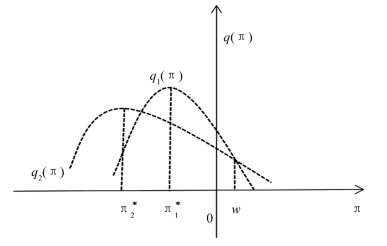
1) 当b(t)-k＞R(t)时，表示股市状态比较好，投资于股票的预期收益率b(t)除掉交易费率仍然比贷款利率R(t)大.

比较公式(14)，公式(15)，注意到π₁^*≥π₂^*＞0，下面分情况讨论.

从图 1可以看出在此种条件下，上界值为

最优投资策略为

对应的HJB方程为

因此可以得出结论：最优的消费和投资解分别由公式(7)和公式(17)给出，其中V(W，T)=h(W，T)是边界条件.

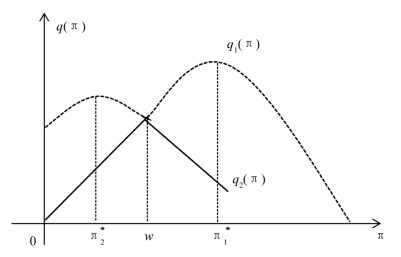
从图 2可以看出，在该种条件下，容易得到最优投资策略为

即这时投资者将全部资产投资于股票，这时上界值的函数形式为

对应的HJB方程

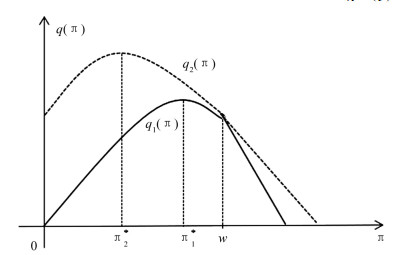
从图 3可以看出，这种条件下上界值为

这时最优投资策略为

对应的HJB方程为

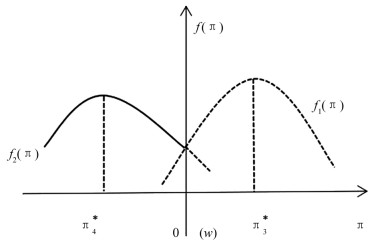
2) 当r(t)＜b(t)-k＜R(t)时，表示股市状态不太好，投资于股票的预期收益率b(t)除掉交易费率大于存款利率，但小于贷款利率R(t).

此时比较公式(14)和公式(15)可知

通过观察图 4并已知贷款利率过高，存款利率较低这一条件，可以发现此时最优决策是投资者把所有财富都用来购买股票，既不需贷款，也不用把资金存入银行，即最优投资策略为

3) 当b(t)-k＜r(t)时，表示股市状态很差，投资于股票的预期收益率b(t)除掉交易费率小于存款利率r(t).此时比较公式(14)和公式(15)可知

从图 5可知，在该种市场状态下投资者会选择谨慎投资，避免在股市出现熊市的时候亏损.为了防止亏空，投资者会选择不买股票，把所有资金都存入银行，这样不仅风险低还能获得一定的利息.此时，最优投资策略为

情形2  π(t)＜0

这种情况只能在市场状况不太好和很差的情况下发生，所以下面分两种市场状态来讨论.

卖空股票时，公式(6)可写为

同样定义

显然

根据公式(26)、公式(27)可得对应的最优投资策略分别为

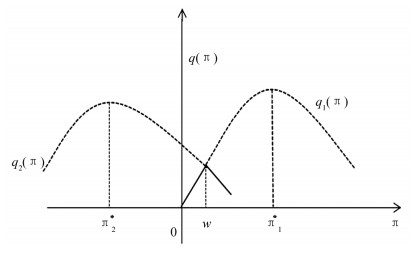
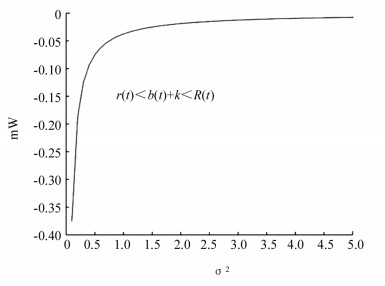
当r(t)<b(t)+k<R(t)时，股票的预期收益率加上交易费率大于存款利率，小于贷款利率，股市状态不太好，比较公式(29)可知

从图 6可以看出，投资者在经过上一期牛市，把资金全部投入到股市后，本期手里持有资金金额为0，此时，投资者应卖空股票以增加现金流，即最优的投资决策为

当b(t)+k＜r(t)时，银行的存款利率比股票的预期收益率大得多，股票市场状态很差，投资者不需要向小额信贷公司贷款，即此时只有W-π≥0的情况，那么根据公式(25)和公式(26)计算出关于π(t)对应的最优值

此时，π₃^*(t)＜0，因为银行的存款利率较高，股票预期收益率较低，市场状态很糟糕，因此投资者的最优决策是卖空|π₃^*(t)|数量的股票，从而将所得的资本利得存入银行账户，资本利得为W-π₃^*.

本文考虑一种经典的效用函数形式HARA，进而计算出最优消费和投资的显式表达，令

其中U，D是常数，A∈(0，1)，γ＞0是贴现率，很容易计算得出

下面先分析买入股票的情况，计算具体的最优消费和投资解.

(1) W≤π₂^*

我们令

则公式(18)可变形为

记

则公式(31)可化简为

两边同除以${\mathit{\Omega }_1}{\left( t \right)^{ - \frac{{A - 1}}{A}}}$并求微分得

先解对应齐次方程，得

由常数变量法，取C₁=z(t)并将上式代入公式(31)，得

则有

又因Ω₁(T)=D，知${C_2} = {{\rm{D}}^{\frac{1}{A}}}$，于是

因此，有

由于W(t)≤π₂^*，可以得到

也就是等价于

经济含义：投资者所持有的财富比较小的最优投资解还小，说明此时投资者没有足够资金用来买入股票，需要向小额信贷公司贷款，因为一般投资者属于风险厌恶型，最多愿意贷款的资金数为π₂^*-W以达到较小的最优值π₂^*.

同样方法可得以下几种情形.

(2) π₂^*＜W＜π₁^*

令

可将公式(21)变形为

解得

式中

因此有

从公式(14)和公式(15)可以得到

又根据π₂^*(t)＜W(t)＜π₁^*(t)，则此时的等价条件为

经济含义：投资者所持有的财富处于两者之间，此时投资者的全部资金可以都用来买入股票，既不需要贷款，也没有剩余资金存入银行.

(3) π₁^*≤W

令

可将公式(24)变为

解上式方程，得

其中

因此有

由于π₁^*(t)≤W(t)，可以得到等价条件

经济含义：投资者所持有的财富比较大的最优投资解还大，此时投资者除了可以买入π₁^*数量的股票，还有剩余的资产可存入银行获得利息收入，存入银行数为W-π₁^*.

而在因市场状态不太好卖空股票时，令

那么，公式(25)变为

解上式方程，得

其中

同理，当市场状态很差时，令

则有

解得

其中

对于以上的讨论，可以得出下面的定理.

定理1  在前面章节的所有假设下，针对最优化问题，根据股票预期收益率较高的市场状态条件，即b(t)-k＞R(t)，并在具体的HARA效用函数形式下，买入股票时给出最优组合策略的显式表达.

其中Ω₁(t)，Ω₂(t)和Ω₃(t)分别由公式(32)，公式(34)和公式(37)给出，值函数的形式为

在市场状态一般的条件下，即r(t)＜b(t)-k＜R(t)，个人投资者的最优投资策略为π^*(t)=W(t)；在市场状态不好的条件下，即b(t)-k＜r(t)，个人投资者的最优投资策略为π^*=0；而在股市状态不太好的时候，即r(t)＜b(t)+k＜R(t)，投资者的最优决策是卖空股票，卖空数为|π₄^*|，最优组合解为

当市场状态很糟糕，即b(t)+k＜r(t)时，投资者最明智的决策就是撤出股市或者因为银行存款利率较高，可将现有资金存入银行，此时最优消费—投资策略为

其中Φ₁(t)，Φ₂(t)分别由公式(39)，公式(40)给出.

从往年中国人民银行公布的存贷款利率数据来看，可以在本文模型中估计出具体的系数值，而在效用函数中的系数则取决于投资者的个人偏好，因此可以利用最优解帮助投资者做出最佳的投资方案.

本文分别模拟在不同的市场状态中，对投资者买入和卖空情况下的数值分析，通过具体的HARA效用函数形式结合模拟数值序列给出最优的投资比例，也可以通过波动率对投资者投资比例的影响这一模拟结果，为投资者分析最优资产决策.

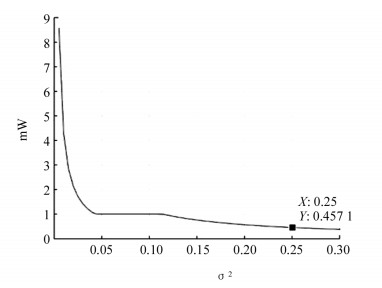
模拟一  在本例中为了简便，令模型中的系数都为常数.假设本模型的时间单位为1年，进而赋值T=1，U=D=0.8，A=0.7，R=0.1，r=0.05，b=0.15，k=0.02.为了方便展示结果，投资者开始买入股票的时刻记为0，模拟结果如图 7.

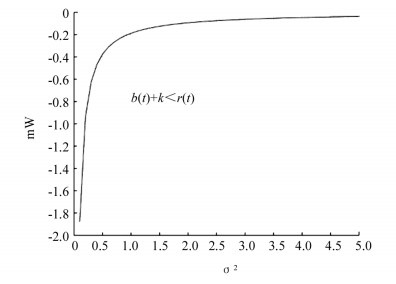
在图 7中，最优投资比例$\frac{{{\pi ^*}}}{W}$曲线根据不同波动率的平方数值分为3个部分.可以看出，当σ²≤0.048，$\frac{{{\pi ^*}}}{W}$关于σ²是单调递减的，即股票价格的波动率越高，投资者投资于股票数占总财富的比例越小，但是因为在这个区间内波动率较小且$\frac{{{\pi ^*}}}{W}$＞1，也就意味着投资者的财富用来购买股票的收益比存入银行所得的利息高，股市状态较好，这会吸引投资者向小额信贷公司借更多的资金从而投资到股市.比如当σ²=0.046，$\frac{{{\pi ^*}}}{W}$大致等于1.5，此时投资于股票的资金是总财富的1.5倍.在第二个区间σ²∈0.048，0.115，$\frac{{{\pi ^*}}}{W}$等于1，这意味着在这一阶段投资者既不需要贷款也没有剩余资金存入银行，将所有财富全部用来购买股票，这和定理1中的第二种情形相吻合.而当σ²≥0.115时，这一比例也是随着波动率的减小而减少，只不过陡峭程度更平缓些.具体而言，当σ²=0.15，$\frac{{{\pi ^*}}}{W}$大致等于0.851时，投资者将其大部分资金投资于股票，小部分存入银行，市场状态一般；而当σ²=0.25，$\frac{{{\pi ^*}}}{W}$=0.457 1时，投资者将其大部分资金存入银行，小部分投资于股票.这也表明随着波动率的不断提高，投资者不愿意冒更大的风险，也就是投资者属于风险厌恶型.

模拟二  ①在b(t)+k＜r(t)的市场状态下，投资者卖空股票时，赋值b=0.05，k=0.02，r=0.1，A=0.8，结果如图 8. ②在r(t)＜b(t)+k＜R(t)的市场状态下，投资者卖空股票时，赋值b=0.05，k=0.02，r=0.05，R=0.1，A=0.8，结果如图 9.

从图 8、图 9可以看出，投资者在面对不同的市场状态时，卖空的股票数占总财富的比例取绝对值，这一绝对值同样随着波动率的平方的增加而减少.当波动率较小时，比例数值变化越明显，在σ²=2.5以后接近平稳.再根据风险偏好系数A的值，表明投资者确属于风险厌恶型.