-
本文仅考虑简单的无向图. 设图G的顶点集为V(G)={1,2,…,n},边集为E(G). 图G的邻接矩阵为A(G)=(aij),其中当ij∈E(G)时,aij=1,否则aij=0. 连接顶点i和j的边的权数用ωij表示,W(G)=(wij)表示图G的广义邻接矩阵,其中当ij∈E(G)时,wij=ωij,否则wij=0. 设NG(i)表示顶点i所有邻点的集合,di=|NG(i)|表示顶点i的度. 若di=0,则称i为孤立点. 若一个图的每个顶点的度均为d,则称这个图为d-正则图. 设D(G)=diag(d1,d2,…,dn)是图G的度对角矩阵. 顶点i的强度
${s_i} = \sum\limits_{j \in V(G)} {{\omega _{ij}}} (i = 1, 2, \cdots , n)$ . 设S(G)=diag(s1,s2,…,sn)是图G的对角强度矩阵. 设Q(G)=S(G)+W(G)和$\mathit{\boldsymbol{L}}(G) = \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{S}}^{ - \frac{1}{2}}}\mathit{\boldsymbol{W}}(G){\mathit{\boldsymbol{S}}^{ - \frac{1}{2}}} = \left( {{l_{ij}}} \right)$ 分别表示加权冠积图G的无符号拉普拉斯矩阵和正规拉普拉斯矩阵,这里众所周知,许多复杂系统,如社会系统、生物系统等,均可用复杂网络来描述,而任何复杂网络都可用图来表示. 因此,关于复杂网络的研究一直是图论领域中的热点问题. 相比较无权网络只考虑节点间相互作用的存在与否,加权网络的权还能刻画该网络所描述实际系统中个体间相互作用的强度,因此加权网络更能准确地描述实际网络[1]. 例如,机场网络[1]中每年在两个机场之间旅行的乘客人数,网络[2]中路由器之间单位时间内的数据包流量,以及生态系统[3]中捕食者——被捕食者相互作用的强度等都可通过权来反映. 虽然目前关于冠图的成果很多[4-8],但关于加权冠图的研究十分鲜见. 文献[9]刻画了G2为d-正则图和完全二部图时加权冠图G1○G2的邻接特征值,同时得到了当G2是连通图时图G1○G2的拉普拉斯特征值. 文献[10]中给出了G2为d-正则图和完全二部图时加权边冠图G1◇G2的邻接特征值和(无符号)拉普拉斯特征值.
受上述研究的启发,本文刻画了当G2为正则图时,加权冠积图G1○G2的无符号拉普拉斯谱,以及G1和G2都为正则图时,G1○G2的正规拉普拉斯谱. 借助数学归纳法,把关于G1○G2的结果加以推广,得到了加权冠图G(m)的无符号拉普拉斯谱和正规拉普拉斯谱. 下面,首先给出加权冠积图[9]的定义.
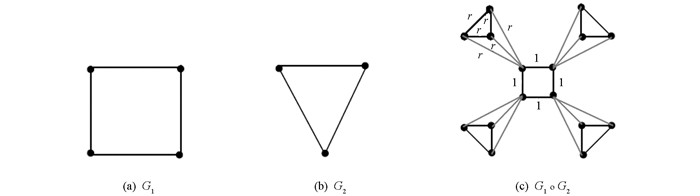
定义1 设G1和G2是阶数分别为n和k的简单连通图,将G1复制一次且每条边的权数为1,G2对应于G1的顶点复制n次且每条边的权数为r(0<r≤1),所得图为加权冠积图G1○G2.
例如,设G1为4个顶点的圈,G2为3个顶点的完全图,则加权冠积图G1○G2如图 1(c)所示.
HTML
-
设R⊗S表示矩阵R和S的克罗内克积,由G1○G2的定义,可得G1○G2的无符号拉普拉斯矩阵为
其中Q(G1)和Q(G2)分别为G1和G2的无符号拉普拉斯矩阵,
${\mathit{\boldsymbol{J}}_k} = (\overbrace {1, 1, \cdots , 1}^k)$ ,In是n阶单位矩阵. 设σ(G)表示G的无符号拉普拉斯谱,当G2是正则图时,首先刻画G1○G2的无符号拉普拉斯谱.定理1 设G1是n阶的简单连通图,G2是k阶的d-正则图. σ(G1)={θ1,θ2,…,θn},σ(G2)={νi|ν1≤ν2≤…≤νk=2d}. 则Q(G1○G2)的特征值为:
(ⅰ)
$\frac{{(2d + 1 + k)r + {\theta _i} \pm \sqrt {{{\left[ {(2d + 1)r - \left( {kr + {\theta _i}} \right)} \right]}^2} + 4k{r^2}} }}{2} \in \sigma \left( {{G_1} \circ {G_2}} \right)$ ,且重数为1,其中i=1,2,…,n;(ⅱ) r(νj+1)∈σ(G1○G2),且重数为n,其中j=1,2,…,k-1.
证 设X=[X1TX2T…Xk+1T]T为Q(G1○G2)的特征值ξ对应的特征向量,其中Xi∈
$\mathbb{R}$ n. 则下面我们分两种情形进行讨论.
情形1 X1为非零向量.
由(1)式和(2)式得
和
其中
${\mathit{\boldsymbol{E}}_i} = (\overbrace {{\bf{0}}, \cdots , {\bf{0}}}^{i - 1}, {\mathit{I}_n}, \overbrace {{\bf{0}}, \cdots , {\bf{0}}}^{k - i}$ .因为G2是d-正则图,则Q(G2)矩阵的每行元素之和为2d. 将(4)式中的所有方程相加,可得
移项得
由于X1是非零向量,我们推出(2d+1)r-ξ≠0. 由(3)式和(6)式,得
即
因此
$\xi - \frac{{k{r^2}}}{{\xi - (2d + 1)r}} - rk$ 是Q(G1)的特征值. 因为σ(G1)={θ1,θ2,…,θn},故可以得到解二次方程(9),得
情形2 X1为零向量.
由(1)式和(2)式得
和
故r(2d+1)不是Q(G1○G2)的特征值. 如若不然,假定r(2d+1)是Q(G1○G2)的特征值,则r(2d+1)对应的特征向量X=[X1X2…Xk+1]T满足X=Jn⊗Jk+1. 因此
这与(11)式相矛盾. 所以
从(12)式可以看出ξ=r(νj+1)的重数为n.
-
正规拉普拉斯矩阵和图G上的简单随机途径与谱的几何结构密切相关. 给定一个图G,令P(G)=D(G)-1A(G)表示G上的简单随机游动的概率转移矩阵,则
设L(G)和P(G)的谱分别为λ1(G),λ2(G),…,λn(G)和μ1(G),μ2(G),…,μn(G). 其中0=λ1(G)≤λ2(G)≤…≤λn(G)≤2,1=μ1(G)≥μ2(G)≥…≥μn(G)≥-1. 则
有关正规拉普拉斯谱的详细信息可参见文献[11].
设G1和G2分别为n1阶和n2阶正则连通图,且正则度分别为r1和r2,则
由于G1和G2都是正则图,故
从而
由(15)式知,在刻画G1○G2的正规拉普拉斯谱时,首先给出概率转移矩阵P(G1○G2)的谱.
定理2 设G1和G2分别是阶数为n1和n2的正则连通图,正则度分别为r1和r2,P(G1)的谱为μ1(=1),μ2,…,μn1,P(G2)的谱为η1(=1),η2,…,ηn2. 则P(G1○G2)的谱为:
(ⅰ)
$\frac{{{r_2}{\eta _j}}}{{{r_2} + 1}}$ ,且重数为n1,j=2,…,n2;(ⅱ)
$\frac{{{r_2}\left( {{r_1} + {n_2}r} \right) + {r_1}{\mu _i}\left( {{r_2} + 1} \right) \pm {\alpha _i}}}{{2\left( {{r_1} + {n_2}r} \right)\left( {{r_2} + 1} \right)}}$ ,且重数为1,i=1,2,…,n1,其中特别地,当μ1=1时,P(G1○G2)的两个特征值分别为1和
$\frac{{{r_1}{r_2} - {n_2}r}}{{\left( {{r_1} + {n_2}r} \right)\left( {{r_2} + 1} \right)}}$ .证 设Z1,Z2,…,Zn2分别为P(G2)的属于特征值η1(=1),η2,…,ηn2的正交特征向量. 当j=2,3,…,n2时,Zj⊥JTn2. 则
设X1,X2,…,Xn1分别为P(G1)的属于特征值μ1,μ2,…,μn1的正交特征向量,即P(G1)Xi=μiXi. 又因P(G2)JTn2=JTn2,故对i=1,2,…,n1,我们有
因此,若两个实数pi和a满足
则P(G1○G2)的属于特征值pi的特征向量为
由(23)式得
由(22)式和(24)式得
其中
若pi(r2+1)-r2=0,则n2=0,那么
${p_i} \ne \frac{{{r_2}}}{{{r_2} + 1}}$ . 因此得到P(G)的2n1个特征值和对应的特征向量. 显然μ1所对应的两个特征值分别为1和$\frac{{{r_1}{r_2} - {n_2}r}}{{\left( {{r_1} + {n_2}r} \right)\left( {{r_2} + 1} \right)}}$ .根据定理2和(16)式,即得出G1○G2的正规拉普拉斯谱:
定理3 设G1和G2分别是阶数为n1和n2的正则连通图,正则度分别为r1和r2,L(G1)的谱为λ1(=0),λ2,…,λn1,L(G2)的谱为δ1(=0),δ2,…,δn2. 则L(G1○G2)的谱为:
(ⅰ)
$\frac{{{r_2}{\delta _j} + 1}}{{{r_2} + 1}}$ ,且重数为n1,j=2,…,n2;(ⅱ)
$\frac{{\left( {{r_2} + 2} \right){n_2}r + {r_1} + \left( {{r_2} + 1} \right){r_1}{\lambda _i} \pm {\beta _i}}}{{2\left( {{r_1} + {n_2}r} \right)\left( {{r_2} + 1} \right)}}$ ,且重数为1,i=1,2,…,n1,其中特别地,当λ1=0时,L(G1○G2)的两个特征值分别为0和
$\frac{{{r_2}{n_2}r + {r_1} + 2{n_2}r}}{{\left( {{r_1} + {n_2}r} \right)\left( {{r_2} + 1} \right)}}$ .
-
本节中,我们将推广加权冠积图得到加权冠图的无符号拉普拉斯谱和正规拉普拉斯谱. 首先,定义加权冠图[9]如下:
定义2 设G是n阶的简单连通图,且每条边的权都为1,G′为G的复制图. 加权冠图G(m)定义为G(m)=G(m-1)○G′,新生成的边的权为rm(其中m≥1是自然数).
例如,设G=K3(3个顶点的完全图)(图 2(a)),则加权冠图G(1)和G(2)分别如图 2(b)和2(c)所示.
由定理1,可以定义函数fj(x):
$\mathbb{R}$ →$\mathbb{R}$ 为其中j=1,2,…,且f0(x)=x+1.
接下来给出当G为d-正则图时,加权冠图G(m)的无符号拉普拉斯谱.
定理4 设G是n阶d-正则图,σ(G)={θ1,θ2,…,θn},则
其中:
j=1,2,…;f0(x)=x+1;rm-jfj(θi)∈σ(G(m))的重数为n(n+1)m-j-1,0≤j≤m-1;fm(θi)∈σ(G(m))的重数为1.
证 用数学归纳法进行证明.
(ⅰ) 当m=1时,设G=G1=G2,由定理1立即得结论成立.
(ⅱ) 当m=k-1时,假设结论成立,即:fk-1(θi)∈σ(G(k-1))(1≤i≤n)且重数为1;rk-j-1fj(θi)∈σ(G(k-1))(1≤i≤n-1,0≤j≤k-2)且重数为n(n+1)k-j-2.
(ⅲ) 当m=k时,由G(k)=G(k-1)○G及定理1可得:fk(θi)∈σ(G(k))(1≤i≤n)且重数为1;rk-j-1fj(θi)∈σ(G(k))(1≤i≤n-1,0≤j≤k-1)且重数为n(n+1)k-j-1;rk(θi+1)∈σ(G(k))(1≤i≤n-1)且重数为n(n+1)k-1. 即:fk(θi)∈σ(G(k))(1≤i≤n)且重数为1;rk-jfj(θi)∈σ(G(k))(1≤i≤n-1,0≤j≤k)且重数为n(n+1)k-j-1.
又由定理3,可定义函数gj(x):
$\mathbb{R}$ →$\mathbb{R}$ 为其中
最后,刻画了G为d-正则图时,G(m)的正规拉普拉斯谱:
定理5 设G是n阶d-正则图,L(G)的谱为λ1,λ2,…,λn,则L(G(m))的谱为
其中
$j = 1, 2, \cdots ;{g_0}(x) = \frac{{dx + 1}}{{d + 1}};{r^{m - j}}{g_j}\left( {{\lambda _i}} \right) \in \sigma \left( {{G^{(m)}}} \right)$ 的重数为n(n+1)m-j-1(0≤j≤m-1);gm(λi)∈σ(G(m))的重数为1.证 同定理4.
-
本文主要研究了加权冠图的无符号拉普拉斯谱和正规拉普拉斯谱. 具体来讲,刻画了当G2为正则图时,加权冠积图G1○G2的无符号拉普拉斯谱,以及G1和G2都为正则图时,G1○G2的正规拉普拉斯谱. 并借助数学归纳法将关于G1○G2的结果加以推广,给出了加权冠图G(m)的无符号拉普拉斯谱和正规拉普拉斯谱. 所得结论进一步丰富了图谱理论和加权网络研究方面的成果.







 DownLoad:
DownLoad: