-
开放科学(资源服务)标识码(OSID):

-
具有高分辨率、空间信息化的降水数据是地球科学、气候学、生态学等相关研究的重要参数[1-5].因地面气象站点的离散性,气候空间模拟成为陆地生态信息空间化研究的重点[4].于贵瑞等[4]从理论和技术层面上提出构建国家尺度、高分辨率栅格化气候信息数据库的基本思路和途径.针对气候要素空间插值算法理论[1-2, 4-9]、精度[4, 6, 8, 10-22]的研究较多,目前常用的降水空间插值法有反距离权重、趋势面、克里金、样条函数、多元回归等10余种[23-26],且有不同的分类[25-26].随着降水机理研究的深入,根据实测降水信息及位置、地形等影响因素进行的空间估计,理论上更加完善[26-27].为获取连续的高精度、高时空分辨率降水数据,在考虑各种降水影响因子的前提下,多源降水信息的融合及多种插值方法的混合使用已成为必然趋势[8, 12, 25],但多源降水信息融合的应用目前仍存在许多不足[28].在引入辅助变量插值时,协同克里格法(Co-kriging)有更大的优势[2, 6, 10, 15, 27, 29-32].
降水属于概率事件,随机性强,与其他气候要素相比,降水空间模拟精度一直倍受关注.除插值方法外,测站数量[19]、分布密度[5, 16, 33]、海陆距离及海拔等宏观地理因子[7, 31, 34-37]、微地形因子[33, 35, 38]、时间分辨率[34]、降水强度[39]等因素也是影响降水空间插值精度的重要因素.研究表明,测站密度越小、气候要素时间连续性越差(如降水),空间化误差越大,冬季误差大于夏季[5].时间分辨率越高,降水空间插值的不确定性越大[34].目前,针对降水概率对降水量空间插值精度的影响,且以实测站点进行验证的研究较少.
内蒙古呼伦贝尔市地域辽阔,地处温带半湿润、半干旱气候区,降水是该区域关键的生态因子和稀缺资源,采用协同克里金(Co-kriging)法进行降水量空间插值,分析该市降水量空间分布特征,探讨降水量插值精度及其影响因素,旨在为呼伦贝尔市及类似地区开展降水量时空动态、水文调控及水资源管理、旱涝灾害监测与评估、农牧业生产指导等,提供高精度降水空间数据及方法参考.
HTML
-
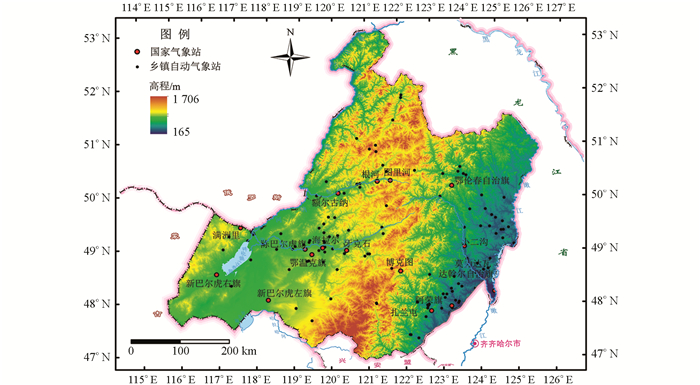
呼伦贝尔市(47°05′~53°20′ N、115°31′~126°04′ E)位于内蒙古自治区东北部,东邻黑龙江,南连兴安盟,北、西北接壤俄罗斯,西、西南接壤蒙古国(图 1).大兴安岭斜贯中部(东北—西南),向东陡降至嫩江平原边缘,向西缓倾至呼伦贝尔高原,海拔约200~1 700 m.呼伦贝尔市以温带大陆性季风气候为主,多年(1961-2018年)气象数据显示,年均温-4.4~3.3 ℃,西南、东南部显著高于中北部山区;年降水量235.6~538.3 mm,东多西少.岭东属嫩江流域,有甘河、诺敏河等嫩江支流,岭西属额尔古纳河流域,主要河、湖有额尔古纳河、海拉尔河、伊敏河及呼伦湖、贝尔湖等.大兴安岭植被以寒温性针叶林(兴安落叶松、樟子松林)为主,兼有蒙古栎、杨、桦落叶阔叶林等;呼伦贝尔高原植被以草原为主,其次为灌丛和草甸等;土壤有灰色森林土、棕色针叶土、暗棕壤、黑钙土、栗钙土等.
-
2018年之前,乡镇自动气象站监测数据不完整,故选择2018年降水观测记录连续性较好的125个乡镇自动气象站作为检测站点,用于插值精度检验.用于空间插值的降水量数据来源于呼伦贝尔市境内的16个国家气象站(图 1)2018年1月1日至12月31日地面站逐日降水量实测数据,分别对年、季降水量空间分布特征进行模拟.
采用Arcmap 10.2中Co-kriging插值模型,考虑地形因素对降水的影响[34],以国家气象站位置(经、纬度)和DEM(分辨率90 m)为协同变量,进行空间插值,模拟呼伦贝尔市年、季降水量时空变化特征.根据检测站位置,“按点提取”各检测站降水量预测值,依据预测值、实测值比值、相关系数以及相对误差(RE)和平均相对误差(MRE)分析降水量空间插值精度.RE和MRE计算公式[18, 22, 34]如下:
式中,xi为第i个站降水量的实测值,xi′为第i个站降水量的预测值,n为检测站数目.RE为站点相对误差值,MRE为n个站点相对误差的平均值.
以实际降水频率(某一时段内有效降水日数占该时段总日数的比例)大小表示降水概率差异.采用线性回归分析年、季降水量空间插值相对误差值与降水频率及宏观地理因子(经度、纬度、海拔)的关系.
1.1. 研究区概况
1.2. 数据与方法
-
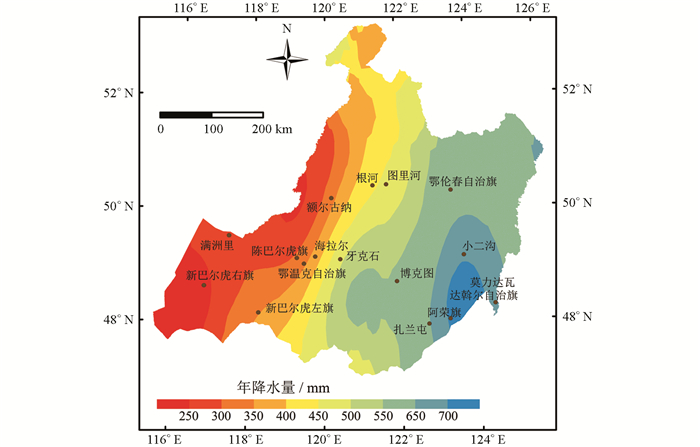
Co-kriging插值结果显示,受季风环流和地形的共同影响,自东向西,呼伦贝尔市2018年年降水量从750 mm左右逐渐降低至220 mm左右,等降水量线延伸方向与大兴安岭走向基本一致,岭东(550~750 mm)显著高于岭西(220~400 mm).2018年年降水量实测值东部最多(阿荣旗765.8 mm),且大于该站多年(1961-2018年)平均年降水量(473.3 mm),西部最少(新巴尔虎右旗224 mm),且小于该站多年(1961-2018年)平均年降水量(235.6 mm),表明该区域2018年年降水量空间差异大于1961年以来的平均模态.除新巴尔虎右旗、陈巴尔虎旗、额尔古纳等少数站点外,多数站点年降水量实测值高于自1961年以来的年降水量平均值,即2018年为多水年(图 2).
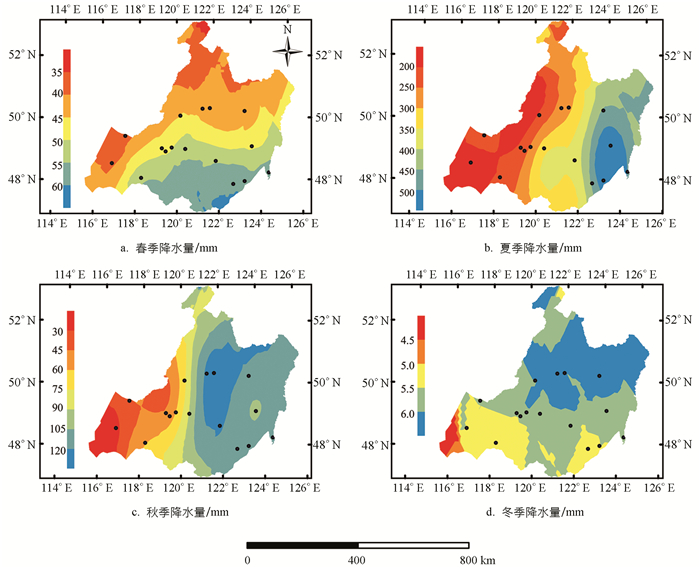
降水量季节分配十分悬殊,冬季(约4.5~6 mm)、春季(约35~60 mm)稀少,夏季丰富(约200~500 mm),70% 以上的降水发生在夏季,秋季较多(约30~120 mm).各季降水量空间分布不均匀(图 3),降水量空间分布差异大小与季节降水量多少有关,多雨区与少雨区降水量之比从大到小依次为秋(4.0)、夏(2.5)、春(1.7)、冬(1.5).春季降水量自南向北递减(图 3a).夏季降水量由东向西显著递减(图 3b),西南新巴尔虎右旗降水量最少,少于200 mm,东南阿荣旗最多,超过600 mm.秋季降水量自东向西显著减小,岭东降水量偏多,尤以大兴安岭东坡最多(博克图121.7 mm、根河139.1 mm、图里河124.5 mm);岭西高原降水量较少,少于80 mm,新巴尔虎右旗降水最少(22.2 mm)(图 3c).冬季降水量最少,空间分布差异亦最小,北及东北部偏多,额尔古纳以东,图里河、鄂伦春均超过6 mm,西南小于5.5 mm,新巴尔虎右旗最少(2.0 mm)(图 3d).
降水量空间分布季节性变化特征主要与东亚季风西伸北进、暖湿气团的季节位移有关.冬、春季降水量较少,降水主要发生在夏、秋季,因此夏、秋季降水量与年降水量空间分布特征相似,均大致表现为自东向西减少的趋势.
-
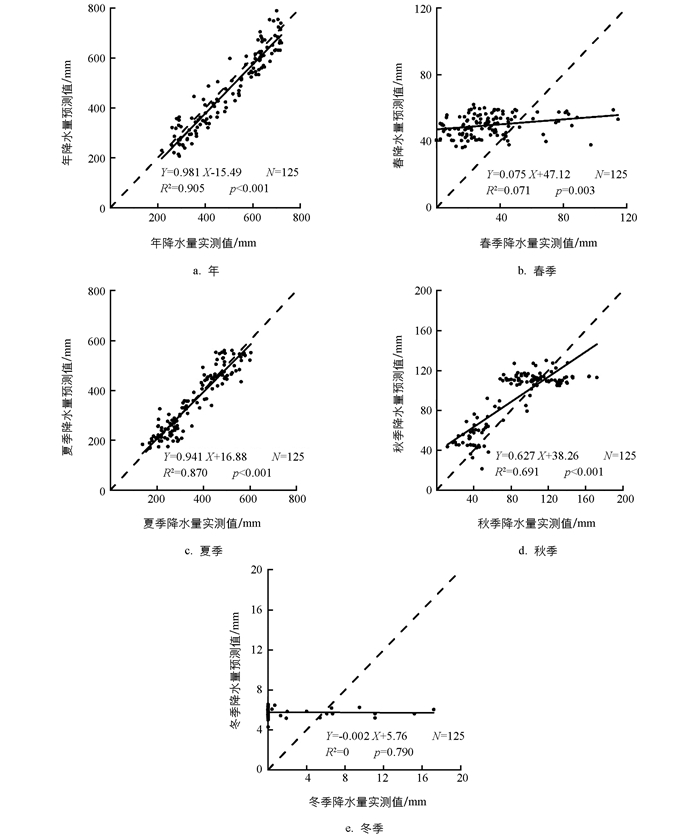
检测站点预测值与实测值分析结果显示,年、夏季降水量预测值与实测值比值分别为0.981,0.942,均接近1(p<0.001),相关系数前者(0.951)略大于后者(0.933),表明空间插值精度年降水量最高,其次为夏季降水量.春、秋季降水量预测值与实测值之比分别为0.075(p=0.003),0.627(p<0.001).春季大部分站点降水量实测值小于预测值,少数站点降水量实测值大于预测值.冬季降水量模拟误差最大,多数站点实测值(0 mm)小于预测值,RE>100%,说明冬季有效降水日数少、降水频率小、随机性强.与已有结论相似[5, 37],降水量空间插值精度表现为年大于季,夏、秋季大于冬、春季.降水量小的季节(春、秋、冬),空间插值法所产生的“平滑效应”明显,即降水量小的站点,预测值大于实测值,降水量大的站点,预测值小于实测值(图 4).
因冬、春、秋季RE较大,故年降水量MRE(11.4%)略大于夏季MRE(10.7%)(表 1).冬、春、秋季降水量相对误差大的检测站点较多,RE超过100% 的站点数分别为115,55,7,降水空间插值不确定性较大.
-
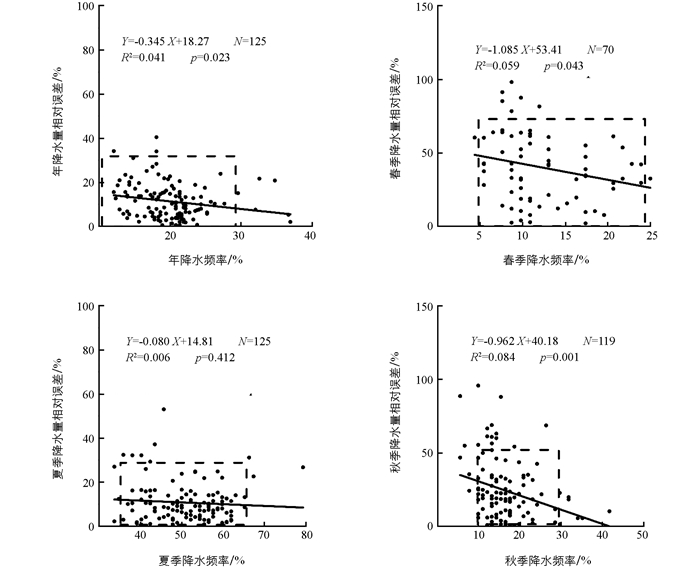
年降水量相对误差最小(RE约0~40%),夏季降水量相对误差(RE约0~60%)次之,春、秋季降水量相对误差较大(部分站点RE>100%),冬季降水量相对误差最大,90%以上站点冬季降水频率为0,RE>100%,降水频率与相对误差相关性分析不具有代表性(故未显示).降水频率与相对误差相关分析表明(图 5),年降水频率与相对误差呈负相关(p=0.023),说明年降水频率越大,相对误差越小,降水量空间插值精度越高.多数站点年降水频率为10%~30%,RE为0~30%.剔除RE>100% 的站点(55个),春季降水频率与相对误差呈负相关(p=0.043).多数站点春季降水频率为5%~25%,RE为0~60%.夏季降水频率最大,多数站点降水频率约35%~65%,RE为0~30%,但夏季降水频率与降水量相对误差无显著相关性(p=0.412),说明影响夏季降水空间插值精度的因素不只是降水频率,可能与有效雨日内降水量多少有关.多数站点秋季降水频率为10%~30%,RE为0~50%,降水频率与降水量相对误差呈显著负相关(p=0.001).
-
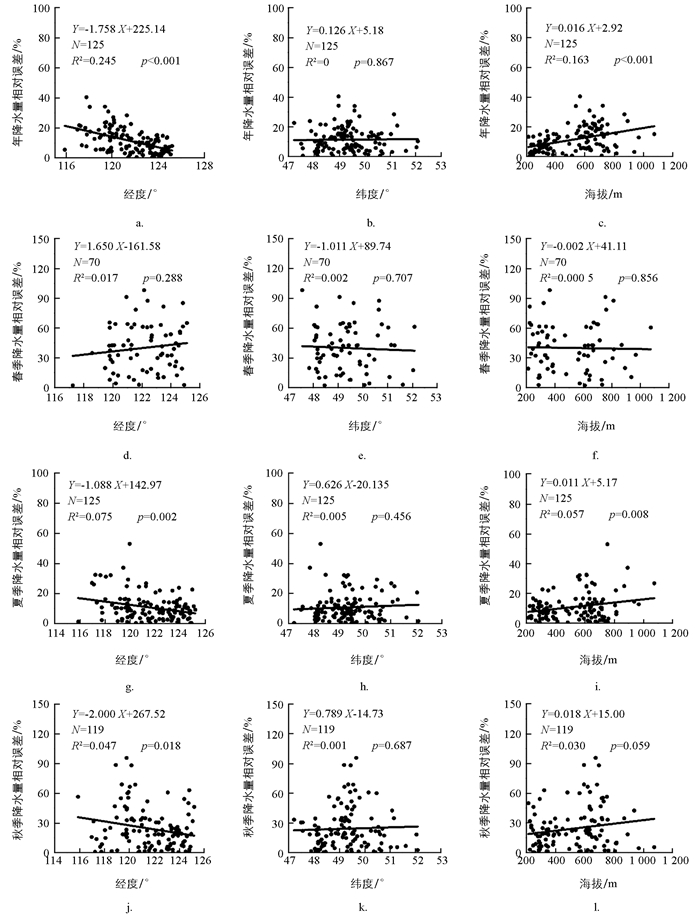
检测站点降水量相对误差与经度、纬度、海拔相关性见图 6.
受季风环流和大兴安岭山地的共同影响,岭东降水频率及降水量大于岭西,且差异有统计学意义,指示降水过程与宏观地理因子有关.宏观地理因子对降水量空间插值精度的影响存在年、季差异,年、季降水量插值精度与纬度相关性较弱(p>0.10),与经度和海拔相关性较强.经度对年、夏季、秋季降水量空间插值精度影响类似,海拔亦然,说明年降水量多少主要取决于夏、秋季降水量的贡献,年、夏季、秋季降水量空间插值精度与湿气团来源、方向及中部山地阻滞有关.年降水量空间插值相对误差与经度呈极显著负相关(p<0.001),与海拔呈极显著正相关(p<0.001),即越向东,年降水概率越大、降水量越多,空间插值相对误差越小、精度越高;海拔越高,年降水量空间插值相对误差越大、精度越低.与之相似,夏季降水量空间插值相对误差与经度呈显著负相关(p=0.002),与海拔呈显著正相关(p=0.008).秋季降水量空间插值相对误差与经度负相关性较弱(p=0.018).冬、春季降水量空间插值相对误差大,主要是降水频率低、强度小所致.
2.1. 降水量空间分布特征
2.2. 降水量空间插值精度
2.3. 降水频率对降水量空间插值精度影响
2.4. 宏观地理因子对降水量空间插值精度影响
-
(1) Co-kriging模拟结果显示,年降水量空间分布及季节动态能够明确指示水汽来源、季风方向以及季风环流对该区域降水过程的影响,突出了降水空间分布受地形影响的显著性,符合降水发生机理.等年降水量线延伸方向与大兴安岭走向基本一致,岭东受夏季风影响明显,降水量偏多,岭西所受影响较小,降水量较少.降水量多少季节差异悬殊,夏、秋季多,冬、春季少.与年降水量空间分布特征相似,夏、秋季降水量呈自东向西递减趋势.
(2) 降水量空间插值不确定性随时间分辨率的提高而增加,降水量插值精度年大于季.四季降水量空间插值精度则为夏、秋季大于冬、春季.年、夏季降水量预测值与实测值之比近于1(p<0.001),空间插值精度较高,次之为秋季,冬、春季降水量小,随机性强,相对误差大、空间插值精度低.说明该区域降水量空间插值精度与降水量多少有关,年、夏季降水量空间模拟更可靠.冬、春季降水量空间插值方法有待改进.
(3) 一般认为降水量大,降水频次就多,本研究显示降水频率对年、春、秋、冬季降水量空间插值精度影响较大,对夏季降水量插值精度影响较小,可能与夏季有效雨日内雨量大小有关.宏观地理因子对降水量插值精度的影响存在年、季差异.年、夏、秋季降水量空间插值精度均随经度增加(向东)而提高,随海拔升高而降低,说明夏季风影响下,距水汽源地越近、降水越多的地方降水量空间插值精度越高.海拔越高、受坡向、风向、湿气团水汽含量等因素影响越复杂,降水量空间插值精度不确定性越大.






 DownLoad:
DownLoad: