-
开放科学(资源服务)标识码(OSID):

-
自适应滤波是统计信号处理的重要组成部分,而稀疏自适应滤波是自适应滤波领域中不可或缺的部分,其显著特征是脉冲响应的大部分分量是零或者接近于零. 在实际场景中,存在大量的稀疏系统,例如数字电视传输通道[1]、回波路径[2]、信道估计[3]等. 由于稀疏系统通常是不确定的,因此需采用基于稀疏系统的自适应滤波算法对其进行辨识[4-5].
应用在稀疏系统中的自适应滤波算法通常采用与稀疏性相关的范数作为稀疏惩罚约束项(Sparse Penalty Constraint,SPC)[6-7],如l1范数,lp范数和l0范数,其中基于l1范数的最小均方自适应滤波算法包括零吸引最小均方(Zero-attracting Least Mean Square,ZA-LMS)算法[8]和加权零吸引最小均方(Reweighted Zero-attracting Least Mean Square,RZA-LMS)算法[9]等,但是ZA-LMS和RZA-LMS的收敛速率较慢,因此,为了提高收敛速率提出了基于零吸引的递归最小二乘(Zero-attracting Recursive Least Squares,ZA-RLS)算法[10]. 通常由于l1范数存在零点处的非光滑性的缺点,会导致算法性能降低,因此,引入lp范数作为SPC提高稀疏系统的滤波精度,进而提出了基于平方根变步长lp范数的LMS算法[11],以变步长的形式分析了稀疏系统中稳态均方误差和收敛速率之间的关系. 通常最小任何lp范数(0<p<1)可等效为最小l0范数,但这是一个非凸优化问题,因此为了解决l0范数中的(Non-deterministic Polynomial,NP)难问题提出了相关熵诱导度量(Correntropy Induced Metric,CIM)用来近似l0范数[12],其典型应用是具有CIM的最大相关熵(Maximum Correntropy Criterion with CIM,CIMMCC)算法[13],CIMMCC算法能够提高非高斯环境下稀疏自适应滤波算法的鲁棒性.
因为非高斯噪声在自然界中是普遍存在的,所以高斯噪声环境下的稀疏算法在非高斯噪声环境下会产生性能不稳定或退化等问题. 从信息理论学习(Information Theoretic Learning,ITL)[14]的观点出发,为解决非高斯噪声对算法性能的影响,提出了广义相关熵(Generalized Correntropic,GC)准则. GC准则本质上是定义在特征空间中相似性度量的一种方法,利用数据的高阶统计特性消除非高斯噪声,其在自适应滤波中最经典的应用是广义相关熵损失(Generalized Correntropic Loss,GC-Loss)算法[15]. 而在稀疏系统中,利用广义最大相关熵准则(Generalized Maximum Correntropy Criterion,GMCC),同时采用CIM作为稀疏惩罚约束项进而提出了具有稀疏惩罚约束的递归广义最大相关熵(Recursive Generalized Maximum Correntropy Criterion with Sparse Penalty Constraint,RGMCC-SPC)算法[16],该算法在CIMMCC算法基础上采用广义递归的更新方式提高了收敛速率和滤波精度. 为了进一步解决RGMCC-SPC算法中非零均值误差在零处误差识别精度较差的问题,提出了可变中心的RGMCC-SPC(Variable Center RGMCC-SPC,RGMCCVC-SPC)算法[17]. 然而由于GC-Loss的性能表面具有高度非凸的特性,导致算法的收敛性能较差. 为了解决这个问题,引入定义在特征空间的核风险敏感损失(Kernel Risk-Sensitive Loss,KRSL)函数[18],使其在非高斯噪声中的性能优于GC-Loss.
启发于KRSL和GMCC,本文提出了一种新的应用在稀疏系统下的广义自适应滤波算法,该算法以广义高斯密度(Generalized Gaussian Density,GGD)[19]函数作为KRSL函数中的核函数,结合稀疏惩罚约束项,以递归的方式进行更新,进而为稀疏系统辨识设计出具有稀疏惩罚约束项的广义递归核风险敏感损失(Generalized Recursive Kernel Risk-Sensitive Loss with Sparse Penalty Constraint,GRKRSL-SPC)算法. 所提出的GRKRSL-SPC算法利用了特征空间中映射数据非二阶统计量的特征,以指数形式强调较大误差的相似性,使得算法在非高斯噪声环境下,能够同时具有强鲁棒性和高滤波精度的特性.
HTML
-
本节在核风险敏感损失函数和广义核风险敏感损失函数的基础上,提出了最小化广义核风险敏感损失函数准则.
-
核风险敏感损失函数是指定义在核空间中两个随机变量X和Y的相似度测量,其表达式如下所示:
其中λ>0是风险敏感参数,E表示期望符号,FXY(x,y)表示关于随机变量X和Y的联合分布函数,kσ(·)是指带宽为σ的Mercer核. 其表达式为
本质上,公式(1)表示核风险敏感损失函数的指数形式只包含二阶统计量,实际上,不同阶的统计量在实际应用中更为普遍. 因此,可以利用广义高斯密度函数作为核风险敏感损失函数的核函数并以此设计广义核风险敏感损失函数.
-
给定如下具有零均值的广义高斯密度函数[19]:
其中,Γ(·)表示伽马函数,b>0是带宽,α>0是形状参数,β=1/bα表示核参数. 从公式(3)可以看出广义高斯密度具有普适性. 当α=1时,广义高斯密度为拉普拉斯分布;当α=2时,则为高斯分布;而当α→∞时,则为均匀分布. 根据文献[15],定义广义相关熵损失函数的表达式为
结合公式(1)和公式(4),可得广义核风险敏感损失函数的表达式为
其中,当0<α≤2时,Gα,b(·)表示为Mercer核,所以在此范围内,广义核风险敏感损失函数可用传统风险敏感损失函数的类似形式重新表示为
其中,Φ(·)表示的是将数据从原始空间转换到核空间H的非线性映射算子,‖·‖H是核空间中的范数. 通过比较式(4)和式(5)可知,式(5)可以看作是广义相关熵损失函数的指数形式. 当α=2时,核风险敏感损失函数是广义核风险损失函数的一个特例,所以,广义核风险损失函数具有普适性. 然而,因为FXY(x,y)通常未知,所以式(5)和式(6)难以计算. 当有L个样本{x(i),y(i)}i=1L可用时,通过计算该L个样本的平均值来获得广义核风险损失函数的近似值,即
-
根据式(5)和式(7),关于广义核风险敏感损失函数的重要性质如下:
1) JG(X,Y)是对称、正定、有界的.
2) JG(X,Y)是具有广义特性的损失函数,在特定情况下可以转换为核风险敏感损失函数、广义熵损失函数和均值P幂误差[20].
证 当α=2时,广义核风险敏感损失函数退化为非广义的形式,风险敏感参数由λ转变为λ/γα,b. 因为存在极限
$ \mathop {{\rm{lim}}}\limits_{x \to {0^ + }} {\rm{exp}}\left( x \right) \to 1 + x$ ,当λ→0+和β→0+时,JG(X,Y)可分别近似于1/λ+JG,C(X,Y)和1/λ+βE[(X-Y)α],即意味着广义核风险敏感损失函数可近似于广义相关熵损失函数和均值P幂误差函数.3) 令e=X-Y=[e(1),e(2),…,e(L)]T,其中e(i)=x(i)-y(i),i=1,2,…,L. 当α>1且β>0时,在任意的|e(i)|≤[(α-1)/(αβ)]1/α处
$ {\hat J_G}\left( {X, {\rm{ }}Y} \right)$ 均具有凸性. 同样地,如果λ的取值超过某一值时,$ {\hat J_G}\left( {X, {\rm{ }}Y} \right)$ 在任意的非零e处也具有凸性. 然而,当β→0+时,在α∈(0,1]情况下,$ {\hat J_G}\left( {X, {\rm{ }}Y} \right)$ 对任意e都是凹面,而当α>1,$ {\hat J_G}\left( {X, {\rm{ }}Y} \right)$ 对任意e都是凸面.证 黑塞矩阵如下:
其中,hi=ξi((α-1)-αβ|e(i)|α)+αβλexp(-β|e(i)|α)|e(i)|α),ξi=
$ \frac{{\alpha \beta {\gamma _{\alpha \beta }}}}{L}|e\left( i \right){|^{\alpha - 2}}$ ×exp(-β|e(i)|α)×exp(γαβ(1-exp(-β|e(i)|α))). 当α>1且β>0,有hi>0;继而对任意e,当|e(i)|≤[(α-1)/(αβ)]1/α,有$ {\mathit{\boldsymbol{H}}_{\hat J}}\left( {{\rm{ }}\mathit{\boldsymbol{e}}{\rm{ }}} \right) \ge 0$ .性质(3)阐述了
$ {\hat J_G}\left( {X, {\rm{ }}Y} \right)$ 的凸性是由参数α,β,λ和e决定的. 风险敏感参数λ控制核风险敏感损失函数的凸范围,λ取值越大,凸范围就越大,通常选择合适β可保证核风险敏感损失函数的凸性. 因此根据$ {\hat J_G}\left( {X, {\rm{ }}Y} \right)$ 的凸性,核风险敏感损失函数更加适合设计自适应滤波器. -
给定一个数学模型,如下所示:
其中,d(i)表示第i时刻的期望输出,Ωo=[Ωo0,Ωo1,…,ΩoL-1]T∈RL×1表示未知系统的最优权重,X(i)=[x(i),x(i-1),…,x(i-L+1)]T∈RL×1是输入信号,ν(i)则代表噪声. 采用Ω表示权重的估计值,基于公式(7),可得如下广义核风险敏感损失函数准则[21]:
通过最小化公式(10)可以获得广义核风险敏感损失函数的最优解,称之为最小化广义核风险敏感损失函数准则,其表达式如下:
其中,
$ {\bf{R}}_{{\bf{XX}}}^g = \sum\limits_{i = 1}^L {} g\left( {e\left( i \right)} \right){\rm{ }}\mathit{\boldsymbol{X}}{\rm{ }}\left( i \right){\rm{ }}\mathit{\boldsymbol{X}}{\rm{ }}{\left( i \right)^{\rm{T}}}$ 是输入信号的加权自相关矩阵;$ {\bf{R}}_{d{\bf{X}}}^g = \sum\limits_{i = 1}^L {} g\left( {e\left( i \right)} \right)d\left( i \right){\rm{ }}\mathit{\boldsymbol{X}}{\rm{ }}\left( i \right)$ 是期望输出与输入信号之间的加权互相关向量,这里g(e(i))=exp(λ(1-exp(-β|e(i)|α)))exp(-β|e(i)|α)|e(i)|α-2.最后,图 1显示了不同α下对广义核风险敏感损失函数曲线平滑度的影响. 从图中可以看出:当误差较小且α值越大时表面越光滑,表明广义核风险敏感损失函数的精度高于非广义形式.
1.1. 核风险敏感损失函数
1.2. 广义核风险敏感损失函数
1.3. 广义核风险敏感损失函数性质
1.4. 最小化广义核风险敏感损失函数准则
-
这一小节主要介绍近似l0范数的稀疏惩罚约束项. 实际上,在寻找最优稀疏项时需要最小化l0范数,而这是一个NP难问题. 通常采用近似l0范数的方法来解决,一种是将其转化为无约束的l1范数正则化问题,可获得近似l0范数的解,但代价是增加采样过程中的测量次数[22];另一种则是采用CIM来近似l0范数,减少了测量中的计算消耗[12],其表达式如下:
其中,σ是核宽. 此外,存在其他近似l0范数的稀疏惩罚约束项为‖Ω‖0≈
$ \sum\limits_{i = 0}^{L - 1} {} (1 - {e^{ - \beta |{\Omega _i}|}})$ [23-24],该方法与CIM之间最显著的区别是指数部分是否为二阶统计量. CIM是具有二阶统计特性,其指数部分权向量能够保证整个函数具有凸性. 基于公平性原则,本文选择了与比较算法相同稀疏惩罚约束项的CIM. 另外,h(i)梯度的向量形式如下: -
定义如下带有稀疏惩罚约束项的广义核风险敏感损失函数为成本函数:
其中,μ表示遗忘因子,ρh(i)代表稀疏惩罚约束项,ρ>0是控制权重向量的稀疏惩罚约束程度的正则化参数. 采用梯度下降法最小化该成本函数,可得:
其中,
令公式(15)的梯度等于0可得权重Ω的解为
根据公式(16),定义Υ(i)和Θ(i)为
根据公式(17)将公式(16)改写为矩阵形式,其权向量可以表示为
Θ(i)通过递归形式进行更新可得:
为了避免计算矩阵的逆运算,根据矩阵求逆引理[25]:(A+BCD)-1=A-1-A-1B(C-1+DA-1B)-1DA-1.
在公式(19)中令A=μΘ(i-1),B=X(i),C=M(i),D=XT(i),可得:
其中,G(i)=
$ \frac{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}{\mathit{\boldsymbol{}}^{ - 1}}\left( {i - 1} \right){\rm{ }}\mathit{\boldsymbol{X}}{\rm{ }}\left( i \right)}}{{\mu + M\left( i \right){\rm{ }}\mathit{\boldsymbol{X}}{^{\rm{T}}}\left( i \right){\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}{^{ - 1}}\left( {i - 1} \right){\rm{ }}\mathit{\boldsymbol{X}}{\rm{ }}\left( i \right)}}{\rm{ }}$ 为卡尔曼增益. 令P(i)=Θ-1(i),公式(20)则可重新表示为所以
采用同样的方法可以得到下列表达式:
将公式(22)两端同时减去ρh′(i),可得:
当迭代至算法性能稳定时,权向量几乎无变化. 即当i→∞时,有h′(i-1)≈h′(i). 所以公式(23)成立.
将公式(21)和(23)代入公式(18)可得权重向量更新式为
最后,根据上述的推导过程,总结GRKRSL-SPC算法如表 1所示.
-
本节分析GRKRSL-SPC算法的计算复杂度,这里考虑每次迭代过程中的加法、除法以及乘法次数. 以α=4为例,各种算法的计算复杂度比较如表 2所示,其中,D表示输入数据的长度,比较算法为基于稀疏惩罚约束的递归广义最大相关熵(Recursive Generalized Maximum Correntropy Criterion with SPC,RGMCC-SPC)算法[16]和基于稀疏惩罚约束的递归广义最大相关熵变中心(Recursive Generalized Maximum Correntropy Criterion with Variable Center under Sparsity Constrained,RGMCCVC-SPC)算法[17]. 从表 2中可知,3种算法具有相同的除法次数,而在乘法和加法运算上,GRKRSL-SPC算法的计算量小于RGMCCVC-SPC算法,但高于RGMCC-SPC算法.
2.1. 稀疏惩罚约束
2.2. GRKRSL-SPC算法
2.3. 计算复杂度分析
-
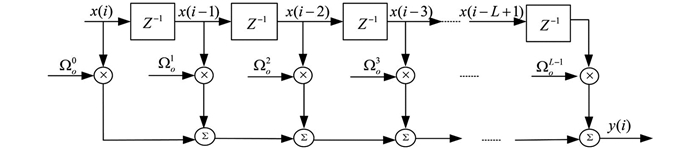
本节将采用蒙特卡洛仿真验证提出的GRKRSL-SPC算法在稀疏系统辨识下的有效性. 未知的稀疏系统中的结构如图 2所示,其中最优权重表示为Ωo=[Ωo0,Ωo1,…,ΩoL-1]T∈RL×1的列向量,输入信号为X(i)=[x(i),x(i-1),…,x(i-L+1)]T∈RL×1的列向量,x(i)表示为第i时刻输入的第一个值,x(i-L+1)则为第i时刻的第L个值,Z-1表示系统的单位延迟. 首先假定自适应滤波器的权重向量是由16个抽头随机产生,将第5个值设置为1,其他值均设置为0,可得稀疏度为1/16,表述为Ωo=[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]T[10]. 其次,设置滤波器的长度为30,系统稀疏度为5/30[16]. 假定自适应滤波器的初始权重向量是零向量,输入信号为单位方差的零均值高斯序列. 噪声模型为:υ(i)=(1-b(i))υ1(i)+b(i)υ2(i),其中υ1(i)是常见的噪声,υ2(i)为较大方差的脉冲噪声,表示大的离群值;b(i)是由伯努利随机过程引起的发生概率,其中概率分布为Pr{b(i)=1}=c,Pr{b(i)=0}=1-c,0≤c≤1,仿真中选择c=0.01. υ2(i)是方差为9均值为0的高斯序列. υ1(i)考虑两种噪声分布:①在{1,-1}范围内的二进制分布,其概率分布为Pr{x=1}=Pr{x=-1}=0.5. ② 2sin(ω)的正弦波,ω满足[0,2π]的均匀分布. 所有仿真结果是在上述混合噪声环境下执行200次蒙特卡洛获得的. 计算机软硬件配置分别为Windows10和Intel(R) Core(TM) i7-8700 CPU 3.20GHz,RAM 8.0G.
在进行实验仿真过程中,为了确保算法比较的公平性,选择在非高斯噪声环境下具有鲁棒性且采用递归更新方式的RGMCC-SPC[16]和RGMCCVC-SPC算法[17]作为比较算法,当RGMCCVC-SPC算法的变中心变为0时退化为RGMCC-SPC算法,设置比较算法的参数使得所有算法具有一致的收敛速率. 为了进一步定量评价滤波精度,定义稳态均方偏差(Mean Square Deviation,MSD)如下,用MMSD表示:
其中,
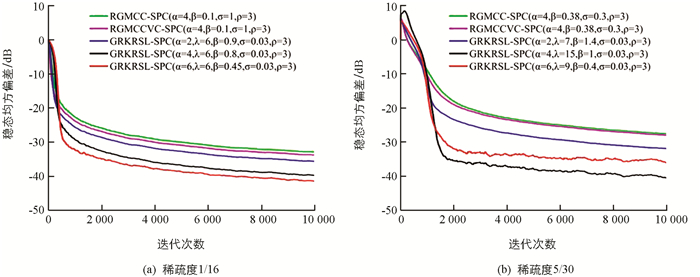
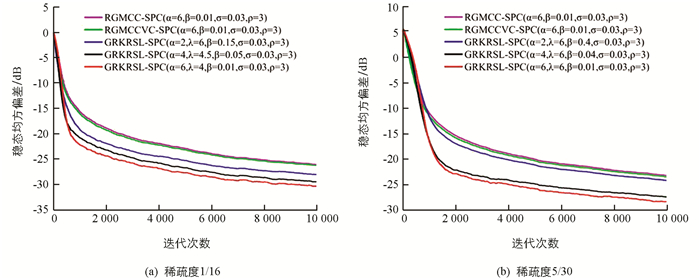
$ {\bf{\tilde \Omega }}$ (i)=Ωo-Ω(i),Ωo为稀疏系统辨识中的最优权重,Ω(i)则是其第i时刻的权重估计值.图 3显示了GRKRSL-SPC算法在二进制噪声下的学习曲线和所有算法的参数设置,其中,图 3(a)和图 3(b)的稀疏度分别为1/16,5/30. 从图 3中可知3个算法在保持几乎一致的收敛速率下,GRKRSL-SPC算法的滤波精度显著高于RGMCC-SPC和RGMCCVC-SPC算法,尤其当α=4和α=6时,表现更明显. 同样地,在稀疏度为1/16和5/30的正弦噪声环境下,GRKRSL-SPC算法提高了稀疏系统辩识中的精度,并且α=4和α=6的滤波性能优于α=2的性能,仿真结果如图 4所示.
表 3显示了在两种稀疏度以及两种噪声环境下算法的消耗时间.
从表 3中可以得出:不论是在二进制噪声还是正弦噪声环境中,GRKRSL-SPC算法比RGMCCVC-SPC算法消耗更少的时间,比RGMCC-SPC算法消耗更多的时间,此结论与表 2中计算复杂度结果相一致. 总而言之,从稳态均方偏差和计算复杂度两方面而言,GRKRSL-SPC算法性能优于RGMCCVC-SPC算法和RGMCC-SPC算法.
-
本文利用广义高斯密度(GGD)函数作为核函数,提出了一种定义在核空间的非线性相似度量方法,即广义核风险敏感损失函数(GRKRSL). 进一步结合递归更新方式提出了应用在稀疏系统模型中的基于稀疏惩罚约束的广义核递归风险敏感(GRKRSL-SPC)算法. 从计算复杂度和滤波精度两个方面去验证了GRKRSL-SPC算法在非高斯噪声环境中的有效性和滤波精度. GRKRSL-SPC算法在保持与RGMCC-SPC和RGMCCVC-SPC算法相同计算复杂度的前提下,提高了稀疏系统的滤波性能,尤其是当α=4和α=6时滤波精度明显提高. 蒙特卡洛仿真结果验证了GRKRSL-SPC算法对稀疏系统识别精度优于其他的鲁棒稀疏自适应滤波算法.







 DownLoad:
DownLoad: