Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2024 Volume 46 Issue 8
Article Contents
Previous Article Next Article

DUAN Tingyi, SHU Lei, ZHAO Hang, et al. Analysis and Optimization Design of Dynamic Performance for Gyrorotor Assembly[J]. Journal of Southwest University Natural Science Edition, 2024, 46(8): 162-171. doi: 10.13718/j.cnki.xdzk.2024.08.015
Citation: DUAN Tingyi, SHU Lei, ZHAO Hang, et al. Analysis and Optimization Design of Dynamic Performance for Gyrorotor Assembly[J]. Journal of Southwest University Natural Science Edition, 2024, 46(8): 162-171. doi: 10.13718/j.cnki.xdzk.2024.08.015
shu

Analysis and Optimization Design of Dynamic Performance for Gyrorotor Assembly

  • 1.

    College of Artificial Intelligence, Southwest University/National & Local Joint Engineering Research Center of ntelligent Transmission and Control Technology, Chongqing 400715, China

  • 2.

    Chongqing God ArrowInertial Technology Co. Ltd., Chongqing 401120, China

More Information
  • Corresponding author: SHU Lei ; 
  • Received Date: 08/11/2023
    Available Online: 20/08/2024

  • MSC: TH133;O318

  • In order to improve the dynamic performance of gyrorotor assembly, the modal response and stress response of a gyrorotor assembly structure were investigated by computer aided engineering (CAE) technology. The lightweight design of gyrorotor assembly structure was carried out, and the dynamic performance of gyrorotor assembly before and after optimization was compared by simulation and test results. The simulation results showed that the modal frequency of the optimized gyrorotor assembly increased significantly compared with that of the pre-optimized gyrorotor assembly, and the average optimization rate of the first 4 modes reached 27.5%. The maximum stress value of the optimized gyrorotor assembly reduced notably compared with that of the pre-optimized gyrorotor assembly, in which the optimization rate was 41.1% along the X axis and 54.6% along the Z axis. The experimental results showed that the drift Y1 caused by the orthogonal pendulum and the drift Y2 caused by the axial mass imbalance of the optimized gyroscope were 63.0% and 84.3% higher than that of the pre-optimized gyroscope, respectively. The simulation results were consistent with the test results, which provides important support for the product development and reliable application of the dynamically-tuned gyroscope.

  • 加载中
  • [1] 郭祖华, 俞文伯. 某挠性接头在路面随机激励下的响应分析[J]. 振动与冲击, 2007, 26(1): 144-147, 154, 167-168. doi: 10.3969/j.issn.1000-3835.2007.01.038

    CrossRef Google Scholar

    [2] XIE B B, JIN Y C, FAHEEM M, et al. Research Progress of Autonomous Navigation Technology for Multi-Agricultural Scenes[J]. Computers and Electronics in Agriculture, 2023, 211: 107963. doi: 10.1016/j.compag.2023.107963

    CrossRef Google Scholar

    [3] 周百令. 动力调谐陀螺仪设计与制造[M]. 南京: 东南大学出版社, 2002.

    Google Scholar

    [4] 董雯霞. 组合式挠性接头角刚度动态测试方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.

    Google Scholar

    [5] 吴瑾颖, 刘光斌. 基于ANSYS的挠性接头有限元模型的建立[J]. 弹箭与制导学报, 2007, 27(2): 53-56. doi: 10.3969/j.issn.1673-9728.2007.02.016

    CrossRef Google Scholar

    [6] 冯永星, 刘涛, 牛红燕, 等. 细颈倾角对挠性接头力学性能影响分析[J]. 应用力学学报, 2012, 29(4): 444-450, 488.

    Google Scholar

    [7] XIA D Z, NI P Z, KONG L. A Digitized Decoupled Dual-Axis Micro Dynamically Tuned Gyroscope with Three Equilibrium Rings[J]. Journal of Electrical Engineering and Technology, 2017, 12(1): 385-395. doi: 10.5370/JEET.2017.12.1.385

    CrossRef Google Scholar

    [8] 金政宏, 陈建, 王炎林, 等. 电动微耕机振动特性分析与减振研究[J]. 西南大学学报(自然科学版), 2021, 43(10): 92-99. doi: 10.13718/j.cnki.xdzk.2021.10.012

    CrossRef Google Scholar

    [9] 李瑞, 武逸凡, 李守太, 等. 基于ANSYS Workbench和ADAMS的振动式花椒采摘机仿真分析及参数优化[J]. 西南大学学报(自然科学版), 2021, 43(12): 57-66. doi: 10.13718/j.cnki.xdzk.2021.12.007

    CrossRef Google Scholar

    [10] GIANNINI D, BONACCORSI G, BRAGHIN F. Size Optimization of MEMS Gyroscopes Using Substructuring[J]. European Journal of Mechanics-A/Solids, 2020, 84: 104045. doi: 10.1016/j.euromechsol.2020.104045

    CrossRef Google Scholar

    [11] RAJARAMAN V, SABAGEH I, FRENCH P, et al. Design, Modelling and Fabrication of a 40-330 Hz Dual-Mass MEMS Gyroscope on Thick-SOI Technology[J]. Procedia Engineering, 2011, 25: 647-650. doi: 10.1016/j.proeng.2011.12.161

    CrossRef Google Scholar

    [12] QIN Z C, DING X K, GE X, et al. A Mode Order Optimized Disk Resonator Gyroscope Considering Thermoelastic Damping[J]. International Journal of Mechanical Sciences, 2022, 236: 107737. doi: 10.1016/j.ijmecsci.2022.107737

    CrossRef Google Scholar

    [13] WU Z Y, FENG R H, SUN C L, et al. A Dual-Mass Fully Decoupled MEMS Gyroscope with Optimized Structural Design for Minimizing Mechanical Quadrature Coupling[J]. Microelectronic Engineering, 2023, 269: 111918. doi: 10.1016/j.mee.2022.111918

    CrossRef Google Scholar

    [14] 郭祖华, 常亮明, 俞文伯. 某型动力调谐陀螺的承载能力分析[J]. 导弹与航天运载技术, 2006(5): 18-23.

    Google Scholar

    [15] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.

    Google Scholar

    [16] 张义民. 机械振动[M]. 2版. 北京: 清华大学出版社, 2019.

    Google Scholar

    [17] YAO Y, ZHU H T, HUANG C Z, et al. Surface Roughness and Topography Analysis in Precision Milling of 3J33 Maraging Steel[J]. Materials Science Forum, 2016, 874: 497-502. doi: 10.4028/www.scientific.net/MSF.874.497

    CrossRef Google Scholar

    [18] 赵嫚, 王荣, 茅健, 等. 马氏体合金钢3J33b磨削力热载荷-晶粒尺寸演变的动态迭代作用机制研究[J]. 表面技术, 2023, 52(7): 217-230.

    Google Scholar

    [19] 孙玉福. 实用工程材料手册[M]. 北京: 机械工业出版社, 2014.

    Google Scholar

    [20] 刘小川, 马君峰, 白春玉, 等. 航空结构动力学研究的进展与展望[J]. 应用力学学报, 2022, 39(3): 409-436, 407.

    Google Scholar

    [21] 孙悦, 刘晓峰, 孙伟. 随机激励作用下硬涂层薄板振动有限元分析及减振预估[J]. 振动与冲击, 2022, 41(4): 63-69.

    Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(11)  /  Tables(5)

Export Citation
PDF
XML

Article Metrics

Article views(1178) PDF downloads(361) Cited by(0)

Access History

Other Articles By Authors

Analysis and Optimization Design of Dynamic Performance for Gyrorotor Assembly

    Corresponding author: SHU Lei ; 
  • Received Date: 08/11/2023
  • Available Online: 20/08/2024

Abstract: 

In order to improve the dynamic performance of gyrorotor assembly, the modal response and stress response of a gyrorotor assembly structure were investigated by computer aided engineering (CAE) technology. The lightweight design of gyrorotor assembly structure was carried out, and the dynamic performance of gyrorotor assembly before and after optimization was compared by simulation and test results. The simulation results showed that the modal frequency of the optimized gyrorotor assembly increased significantly compared with that of the pre-optimized gyrorotor assembly, and the average optimization rate of the first 4 modes reached 27.5%. The maximum stress value of the optimized gyrorotor assembly reduced notably compared with that of the pre-optimized gyrorotor assembly, in which the optimization rate was 41.1% along the X axis and 54.6% along the Z axis. The experimental results showed that the drift Y1 caused by the orthogonal pendulum and the drift Y2 caused by the axial mass imbalance of the optimized gyroscope were 63.0% and 84.3% higher than that of the pre-optimized gyroscope, respectively. The simulation results were consistent with the test results, which provides important support for the product development and reliable application of the dynamically-tuned gyroscope.

    HTML

  • 开放科学（资源服务）标识码（OSID）：

  • 动力调谐陀螺仪是一种用于测量物体旋转运动和姿态的高精度传感器设备，因其具有小尺寸、高精度、长寿命和高可靠性等优点，广泛应用于智慧农业、航空航天、船舶导航以及无人驾驶汽车等领域[1-2]. 动力调谐陀螺仪通过挠性轴支撑陀螺转子，并依靠内外挠性轴上4组正交细颈结构的弹性变形实现陀螺转子偏转，从而测量物体的角速率[3-4]. 在这一工作过程中，所产生的载荷均由与其相连的陀螺转子，即挠性接头上的细颈结构体所承受，因此陀螺转子作为动力调谐陀螺仪的关键组件，其结构性能至关重要. 目前围绕动力调谐陀螺仪陀螺转子组件结构性能研究的公开文献较少，在已有文献中，吴瑾颖等[5]探究了挠性陀螺仪扭杆细颈的刚度性能，通过静力学分析和模态分析来查找不同尺寸参数挠性接头的关键受力位置，结果表明扭杆细颈是挠性接头的最薄弱环节. 冯永星等[6]对单平衡环挠性接头的力学性能进行了分析，探究了不同倾角细颈结构的冲击响应和刚度性能，结果表明当细颈倾角为44°时，挠性接头的综合表现最好. Xia等[7]提出了一种新型的数字化解耦双轴三平衡环微动力调谐陀螺仪，并建立了该陀螺仪的力学和运动学模型，通过理论分析和ANSYS仿真分析对结构参数进行了优化，验证了其可靠性. 事实上，在实际应用中，陀螺仪面临着各种各样复杂的场景工况，这对陀螺仪的动态特性提出了非常高的要求，而上述研究尚未涉及到复杂工况对结构真实影响的探究.

    计算机辅助工程(Computer Aided Engineering，CAE)技术目前已作为一种成熟且高效的研究手段广泛应用于结构研究领域[8-9]，该技术被证实能够有效开展各种陀螺仪结构的动态响应特性研究，并能够提供良好的解决方案[10-13]. 因此，本文采用CAE技术来考察某陀螺仪陀螺转子组件结构的模态响应以及应力响应情况，基于得到的仿真结果对陀螺仪陀螺转子结构进行优化设计，并与优化前结构的仿真和试验结果进行比较，以证实优化后陀螺转子结构的性能优势，为动力调谐陀螺仪的产品开发和可靠应用提供重要支持.

1.   陀螺转子结构

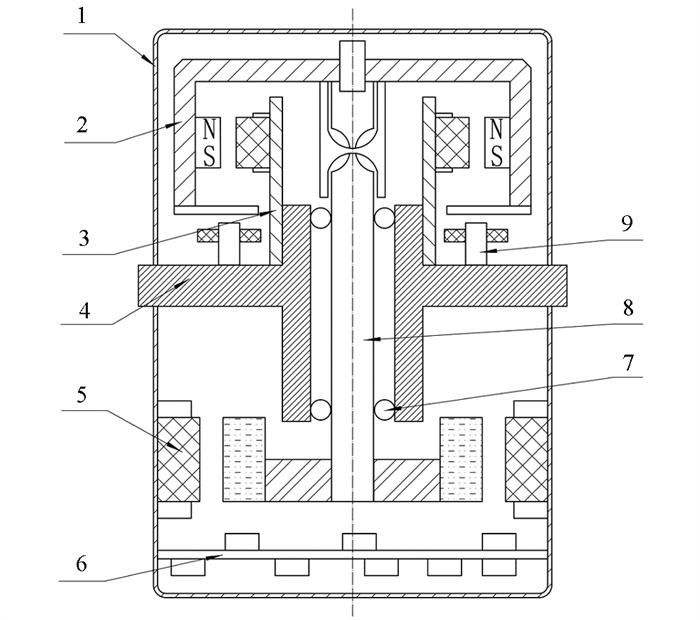
  • 某型号动力调谐陀螺仪的结构如图 1所示，主要由陀螺转子组件、力矩器组件、基座、驱动电机组件、电路板等组成. 该陀螺仪是一种用高速陀螺转子的动量矩敏感基座相对惯性空间绕正交于驱动轴的二自由度角运动检测装置. 其中驱动电机组件为陀螺转子组件提供高速旋转的动力，信号器用于检测基座相对于陀螺转子组件自转轴的偏角，并提供输出信号，力矩器组件用于对陀螺转子组件施加控制力矩，并使陀螺转子组件进动或保持稳定方位. 陀螺转子组件结构将直接影响整个陀螺仪的角运动检测性能.

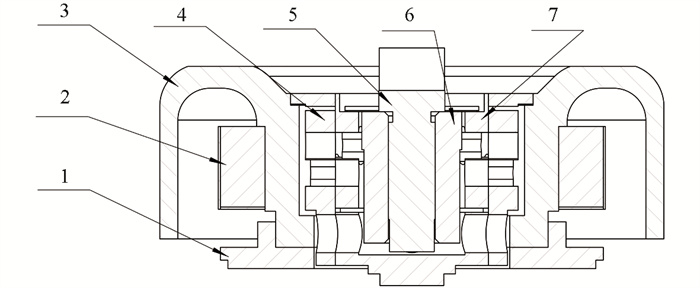
    陀螺转子组件作为动力调谐陀螺仪的关键部件，其结构示意如图 2所示，包括内挠性接头、外挠性接头、螺钉座、调谐螺钉、磁钢、转动轮、跟随转子. 其中内、外挠性接头与螺钉座以及外挠性接头与转动轮采用激光焊接工艺方法保持其之间相对固定. 磁钢、跟随转子与转动轮结构体采用胶接工艺方法保持其之间相对固定. 调谐螺钉通过螺纹与螺钉座紧密配合. 当陀螺转子组件在旋转过程中受到外力时，陀螺转子组件会绕内(或外)挠性接头轴线发生偏转，此时内(或外)挠性接头细颈产生弹性变形.

2.   陀螺转子组件动力学分析

    2.1.   动力学基本理论

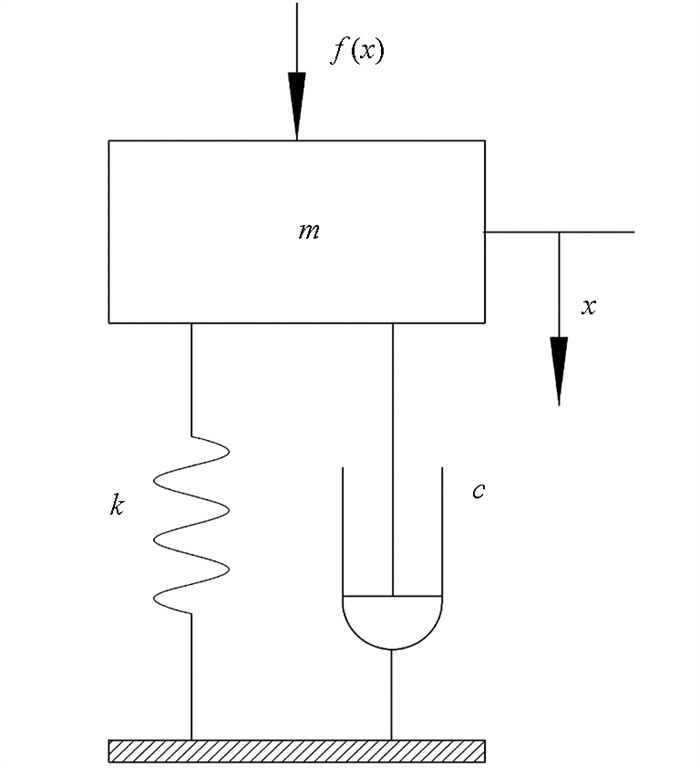
  • 陀螺转子组件可简化为质量-弹簧系统，如图 3所示.

    图中，k为细颈结构静刚度；c为细颈结构阻尼；m为承载的质量体，该质量体m包括转动轮、磁钢、跟随转子、螺钉座和调谐螺钉；内外挠性接头的细颈类似于连接在质量体m上的弹簧.

    整个陀螺转子组件的固有频率表达式为

    作为有阻尼的质量-弹簧系统，其动态方程可表示为：

    假设该系统的振动由不同频率的简谐振动组成，令其解的形式为：

    式中：xm为振幅；ω为外部激励角频率；φ为振动相位角. 则有：

    陀螺转子组件在动态过程中的振幅如下[16]：

    式中：F(ω)为振动过程中的外部激励.

    • 2.2.   有限元模型建立

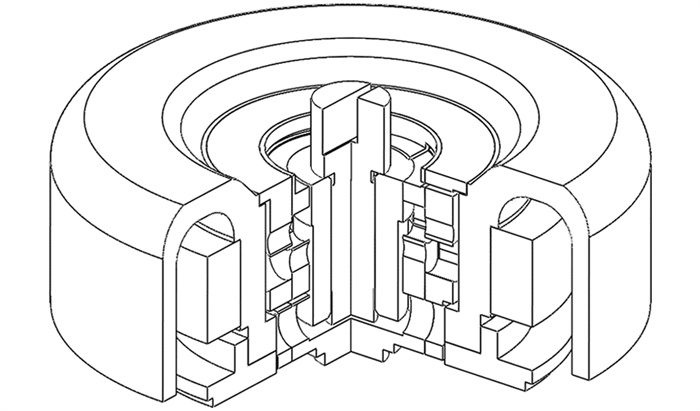
  • 采用SolidWorks软件建立陀螺转子组件三维模型，在此过程中，保证每个零件具体结构以及相对位置关系与实物一致. 陀螺转子组件三维模型如图 4所示.

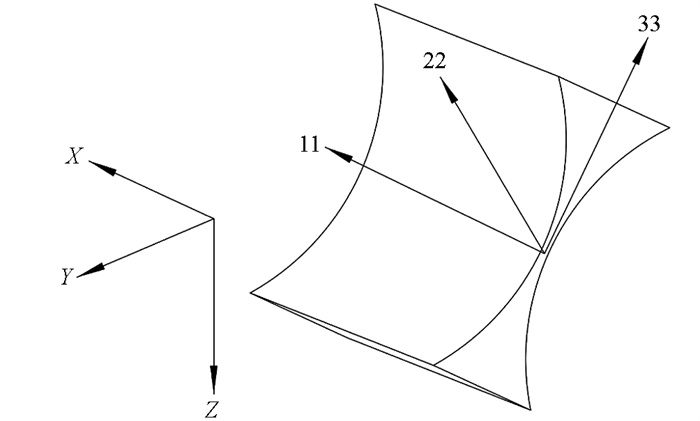
    将几何模型导入ABAQUS有限元分析软件，进行有限元网格划分. 由于结构主要应力区域为内、外挠性接头细颈部位，为了获得准确的应力结果，需要确保该部位网格足够致密且具有高质量，因此在细颈位置采用六面体网格单元划分. 由于陀螺转子组件各零件结构较为复杂，具有较多细小特征，为了更好地适应各种结构的几何形状，同时提高前处理效率，除细颈位置以外的其他结构区域采用四面体网格划分. 最终划分的陀螺转子组件及细颈局部网格模型如图 5所示，网格总单元数为154 608，总节点数为43 797. 此外，考虑到细颈外形结构方向与绝对坐标系不重合，为了便于后期查看计算结果，对细颈赋予材料坐标方向，局部材料坐标方向如图 6所示(11，22，33)，其中11方向为内外挠性接头壁厚方向，22方向为细颈厚度方向，33方向为细颈弯曲正应力方向.

    • 2.3.   输入参数与分析设置

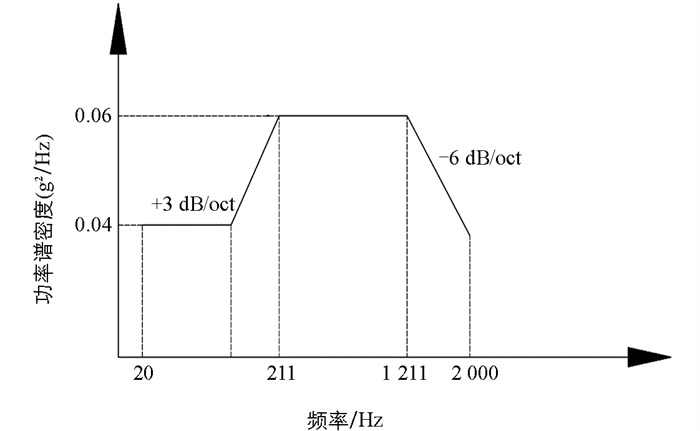
  • 内、外挠性接头为陀螺转子组件的关键零件，因此其材料选用高强度弹性合金3J33B. 该材料与其他弹性合金相比，所含合金元素较少，却具有优异的综合性能，即具有较高的弹性极限、大储能比、低内耗、较小的弹性模量温度系数、良好的耐疲劳性，同时具有抗应力腐蚀和抗冲击性能，并具有良好的热稳定性和加工性能[17-18]. 在ABAQUS-Property模块中设置各材料的密度、弹性模量和泊松比，详细参数见表 1. 根据实际接触情况，在ABAQUS-Interaction模块中设置所有零件之间接触关系为绑定接触(Tie连接). 根据实际安装要求，陀螺转子组件通过驱动轴固定在基座上，驱动轴与内挠性接头相连，因此在ABAQUS-Load模块中设置内挠性接头底部为固支边界条件(Fixed约束)，并在该底部施加随机振动激励. 随机振动输入条件(PSD功率谱密度曲线)如图 7所示. 由图 7可知，随机振动条件施振频率最高为2 000 Hz，因此模态分析主要关注2 000 Hz以内的振型结果.

    • 2.4.   动力学结果

    2.4.1.   模态结果

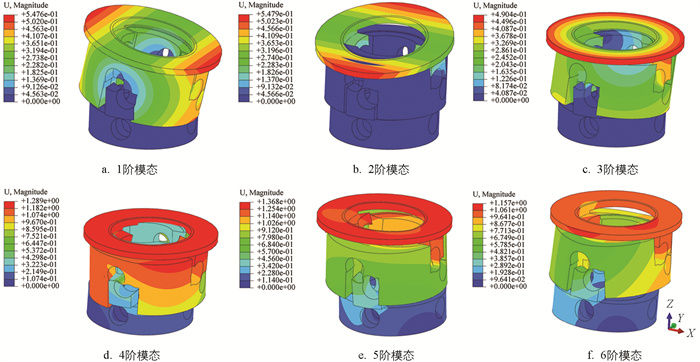
  • 陀螺转子组件的模态分析结果如图 8和表 2所示. 由模态分析结果可知，结构的1~2阶模态为陀螺转子绕相对2组正交细颈结构连线的偏转，该模态变形下挠性接头细颈为单纯的弯曲振型，且结构的1~2阶固有频率不到30 Hz，数值稍低；结构的3~6阶模态同样集中在细颈结构附近，除相应的固有频率不同外，对应的正交细颈结构不再是单纯的弯曲振型，而是弯曲与扭转的组合振型，对细颈结构的动态性能要求更高. 上述振型结果也证实了挠性接头细颈为陀螺转子组件结构最薄弱的环节，在后续的随机振动分析中需要额外关注.

    • 2.4.2.   随机振动结果

  • 以上述模态结果为基础，采用模态叠加法在ABAQUS/Standard软件中对陀螺转子组件进行随机振动响应分析. 由于陀螺转子组件在实际工作环境中一直处于高速旋转状态，且基于模态叠加的随机振动分析不支持阻尼模态，为了确定最危险的加载方向，须对陀螺转子组件的不同姿态进行加载计算. 根据文献及上述分析可知，陀螺转子组件力学性能由细颈上的承载能力决定[6]，因此本文主要关注不同旋转角度姿态加载情况下挠性接头细颈的应力分布.

    随机振动载荷输入条件按照坐标轴方向进行加载，为了节约计算资源，在X轴向加载时，将陀螺转子组件每转动30°计算一次响应，考虑到陀螺转子组件结构的对称性，只需计算0°~180°旋转角度范围内的姿态即可. Y轴向加载与X轴向加载类似，不再重复计算. 当载荷方向为Z轴向时，不存在上述问题. 表 3给出了X轴向和Z轴向加载时，陀螺转子细颈区域在不同角度姿态下随机振动响应的最大应力结果. 其中，R11，R22，R33分别表示细颈局部材料坐标方向的均方根应力值.

    由表 3可知，载荷方向沿X轴向加载时，旋转角度30°为陀螺转子组件的最危险姿态，此时陀螺转子组件发生了弯曲与扭转的组合变形，其中在33材料方向上的应力值最大，其最大应力值R33为445 MPa. 当沿Z轴向加载时，最大应力值R33为301.3 MPa. 在实际工作中，随机振动载荷是一个时间历程上的作用力，内、外挠性接头细颈会受到载荷的多次作用，导致细颈位置疲劳损伤. 3J33B金属材料的疲劳极限为685 MPa[19]，上述X、Z轴向最大应力值R33对应的损伤值偏大，细颈结构较危险. 因此，为了减小随机振动重复载荷作用的疲劳损伤，须减小细颈位置单次载荷的数值大小，从而提高整个陀螺转子组件的动态性能.

3.   陀螺转子优化设计

  • 根据广义胡克定律并结合式(5)可得陀螺转子组件的动刚度(位移阻抗)为：

    结构的动刚度kd(ω)越大，对应的结构响应振幅xm(ω)越小，则细颈承受的应力越小，因而相同量级振动下，陀螺转子组件的动态性能越高. 由式(6)可知，陀螺转子组件的动刚度kd(ω)主要与结构静刚度k、阻尼c和外部激励频率ω以及结构质量m有关. 在一定的外部激励频率ω下，为了提高陀螺转子组件的动刚度kd(ω)，可以增大结构静刚度k，阻尼c以及减轻结构质量m. 当结构材料一定时，由于结构静刚度k是陀螺转子组件2倍频角振动引起的漂移误差主要因素，增大结构静刚度k可能会带来更大的陀螺转子组件漂移误差. 阻尼c与结构形状的关系很复杂，难以直接通过提高阻尼c来改善陀螺转子组件的动刚度kd(ω). 因此，减少结构质量m是提高陀螺转子组件动刚度kd(ω)最直接、最高效的优化手段.

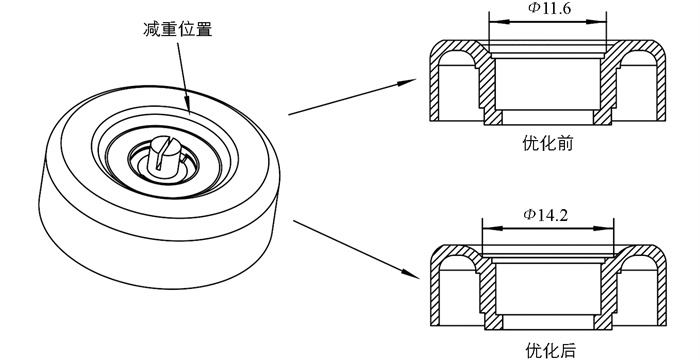
    结构质量m为转动轮、磁钢、跟随转子、螺钉座和调谐螺钉的总质量. 改变磁钢的外形尺寸会影响陀螺转子组件的磁性能；改变螺钉座和调谐螺钉的质量会影响陀螺转子组件的调谐频率；改变跟随转子结构会影响陀螺仪信号输出；同样地，改变细颈结构尺寸会严重影响挠性接头的正弹性系数，从而影响陀螺转子组件的质量指标. 综合考虑，对转动轮结构进行轻量化设计是减轻结构质量m的最优选择，通过降低转动轮质量，能够降低转动轮的惯性矩，进而减小细颈位置单次载荷的数值大小. 根据陀螺转子组件结构实际情况，结合图 2和图 4进行分析，若考虑加大转动轮内圆直径来减小质量，则会引起外挠性接头几何外形的改变，从而降低转动轮的结构强度；若考虑去除转动轮与跟随转子配合处的部分材料，则会引起跟随转子几何结构改变，从而影响陀螺仪的信号输出；若考虑减小转动轮与磁钢配合处圆柱直径，则会引起磁钢外形尺寸改变，从而影响陀螺转子组件的磁性能；若考虑减小转动轮最大外圆直径，则会导致转动轮外圆壁厚变薄，极大地提高了加工难度. 因此，转动轮的最佳减重区域聚焦在其上端面中心区域，对该区域进行部分材料去除不会引起其他配合零件外形尺寸改变，同时也不会对转动轮结构强度以及加工难度产生影响. 综上，本文选择对转动轮上端面中心区域的过渡圆尺寸进行扩大. 在优化设计过程中，一方面希望结构减重比例超过10%(此时过渡圆直径应大于14.0 mm)；另一方面考虑到薄壁零件的加工变形以及结构强度要求，结合结构应力预仿真结果、产品设计准则以及工程师经验，最小壁厚不应小于1 mm(此时过渡圆直径不超过14.4 mm)，因此，本文取中间数值14.2 mm作为优化尺寸. 最终确定过渡圆直径由11.6 mm变为14.2 mm，其结构改变细节如图 9所示. 最终，优化后转动轮质量为9.1 g，相比优化前转动轮质量10.2 g，减重比率达到10.8%.

4.   优化前后陀螺转子仿真结果对比

    4.1.   模态频率结果对比

  • 采用相同的方法及条件对优化前后陀螺转子组件结构进行CAE分析，得到了如表 4所示的模态频率数据(第5阶固有频率超过2 000 Hz，不再关注). 由表 4可知，优化后的陀螺转子组件相比优化前的陀螺转子组件其动态性能有很大提升. 其中最受关注的前2阶固有频率分别为36.6 Hz和37.6 Hz，优化率均超过了28%；第3阶和第4阶模态频率也均有近似程度的提升；前4阶模态频率平均优化率达到了27.5%.

    • 4.2.   随机振动结果对比

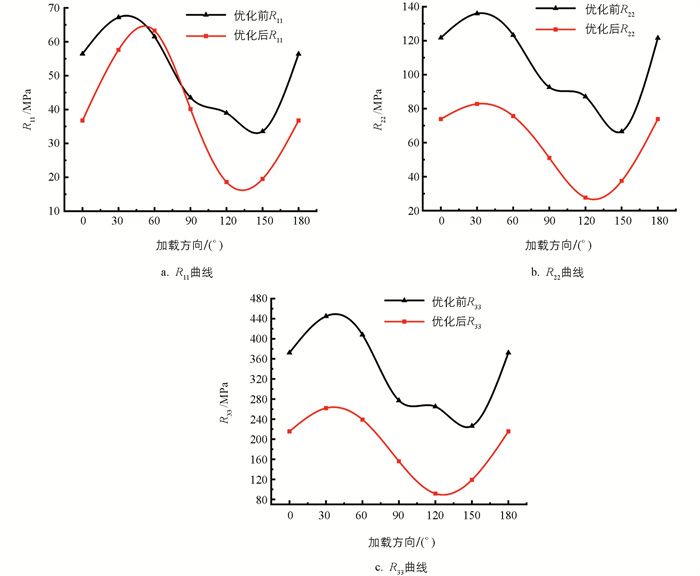
  • 随机振动条件下，优化前后陀螺转子细颈各加载方向的R11、R22、R33对比曲线如图 10所示. 由图 10可知，对陀螺转子组件进行结构优化后，并未改变其随机振动加载时最危险姿态对应的方向，同时优化前后细颈各加载方向的R11，R22，R33变化趋势基本一致. 当载荷方向沿X轴向加载时，优化后陀螺转子组件结构在33材料方向上的最大应力值R33为262 MPa，相比优化前结构在33材料方向上的最大应力值R33降低了183 MPa，优化率为41.1%. 当载荷方向沿Z轴向加载时，优化后陀螺转子组件结构在33材料方向上的最大应力值R33为136.9 MPa，相比优化前结构在33材料方向上的最大应力值R33降低了164.4 MPa，优化率为54.6%. 从上述仿真结果来看，本次针对陀螺转子组件结构的优化设计是有效的，极大提高了其结构的动态性能.

5.   优化前后陀螺仪抗振性能试验对比

    5.1.   试验目的与方法

  • 为了进一步验证上述结论，对优化前后的陀螺仪进行抗振性能测试，该测试能够有效估计结构的动态响应特性[20-21]. 采用五轴加工中心(I-600，Mazak公司，日本)对优化后陀螺转子组件的转动轮结构进行加工，并对陀螺转子组件进行装配，然后将优化前后的陀螺仪安装在同一振动试验台(DC-600-6，苏试试验仪器有限公司，中国)进行抗振动性能对比试验，如图 11所示. 为了使振动效果更显著，将试验输入条件放大3倍，每次试验均在3个轴向分别进行加载，每个轴向施振5 min，施振完成后进行数据测量，共计试验5次.

    • 5.2.   试验结果及分析

  • 试验过程中，直接测量陀螺转子组件细颈的受力情况难度比较大，根据文献[3]给出的陀螺转子组件抗振性能评价指标，采用正交摆性引起的漂移Y1和轴向质量不平衡引起的漂移Y2来对其动态性能进行定量评价，试验结果见表 5.

    由表 5可知，随机振动试验条件下，优化前的陀螺仪正交摆性引起的漂移Y1和轴向质量不平衡引起的漂移Y2分布范围分别为0.34~3.24 h/g与-2.28~4.87 h/g，标准差分别为1.08 h/g与3.45 h/g；优化后的陀螺仪Y1和Y2分布范围分别为-1.81~-0.80 h/g与3.07~4.23 h/g，标准差分别为0.40 h/g与0.54 h/g. 优化后的陀螺仪相比优化前的陀螺仪Y1提升了63.0%，Y2提升了84.3%，因而具有更佳的动态性能. 试验结果与仿真结果具有一致的评价，再次验证了陀螺转子组件结构优化设计的有效性和可行性.

6.   结论

  • 本文采用CAE技术，考察了某陀螺仪陀螺转子组件结构的模态响应以及应力响应，结合轻量化理论对陀螺转子组件结构进行优化设计，得出如下结论：

    1) 优化后的陀螺转子组件前2阶固有频率分别为36.6 Hz和37.6 Hz，相比优化前的陀螺转子组件其优化率均超过了28%；第3阶和第4阶模态频率也均有近似程度的提升，前4阶模态频率平均优化率达到了27.5%.

    2) 沿X轴向加载时，优化后陀螺转子组件结构在33材料方向上的最大应力值相比优化前结构的最大应力值降低了183 MPa，优化率为41.1%；沿Z轴向加载时，优化后陀螺转子组件结构在33材料方向上的最大应力值相比优化前结构的最大应力值降低了164.4 MPa，优化率为54.6%，仿真结果表明了本次优化设计的有效性，极大提高了陀螺转子组件结构的动态性能.

    3) 随机振动试验条件下，优化前的陀螺仪正交摆性引起的漂移Y1和轴向质量不平衡引起的漂移Y2分布范围分别为0.34~3.24 h/g与-2.28~4.87 h/g，优化后的陀螺仪Y1和Y2分布范围分别为-1.81~-0.80 h/g与3.07~4.23 h/g，优化后的陀螺仪相比优化前的陀螺仪Y1提升了63.0%，Y2提升了84.3%，因而具有更佳的动态性能.

    4) 仿真结果与试验结果具有一致的评价，验证了本文对陀螺转子组件结构优化设计的有效性和可行性，为动力调谐陀螺仪的产品开发和可靠应用提供了重要支持.

Figure (11)  Table (5) Reference (21)

Catalog

    Copyright Journal of Southwest University Natural Science Edition

    Address： Tel：023-68254576, 68252540, 68366165,68366917 E-mail：lkxb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return