-
开放科学(资源服务)标识码(OSID):

-
山区流域暴雨极易造成洪水灾害, 因此洪水预报工作至关重要。除了采用传统的预报方法外, 也可采用深度学习循环神经网络(Recurrent Neural Networks, RNN)洪水预报模型进行预报, 长短时记忆神经网络(Long Short Term Memory, LSTM)模型就是其中的一种。文献[1]在一般RNN理论的基础上, 提出了LSTM网络。近年来有不少学者开始把LSTM网络应用于水文序列的预测[2]。文献[3]将LSTM和BP两种模型相结合进行降雨径流预测, 预报精度符合要求。文献[4]比较了长短期记忆网络、一般循环网络、回声状态网络以及GR4J模型的日径流模拟效果, 结果表明LSTM模型在中小流域降雨径流预报中效果更好。文献[5]对比了LSTM与萨克拉门托模型的径流预测结果, 相对来说前者模拟效果更好。文献[6]采用LSTM网络研究受上游水库泄洪影响的Mekong河径流预测工作, 预测结果良好。文献[7]建立了LSTM洪水预报模型, 其表现出的效果比新安江模型好。文献[8]构建了三峡水库LSTM洪水预报模型, 其效果优于BPNN和动态神经网络模型。文献[9]构建了MPGA-LSTM径流预测模型, 对石砻站2013-2017年逐月径流过程进行预测, 精度达到甲级标准。文献[10]利用渡里站逐时降雨和流量数据构建BP和LSTM网络进行流量预报, 结果表明后者整体预报效果优于前者。文献[11]构建了考虑时空分布变化的SLA-LSTM模型, 效果优于卷积网络模型。文献[12]将经验模态分解方法和LSTM网络相结合, 使模型的模拟效果显著提升。文献[13]利用径向基函数(RBF)网络和降雨方差对洪水进行分级, 建立LSTM洪水预报误差校正模型, 对分级洪水预报结果进行校正, 效果较好。文献[14]针对不同预见期建立白盆珠流域LSTM模型, 并与新安江模型进行对比, 证明了LSTM网络具有较高的预报精度。文献[15]引入LSTM网络建立大汶河流域洪水预报模型, 预测结果较好。文献[16]建立AR和LSTM误差校正模型, 对预报流量进行误差校正, 结果表明LSTM模型效果优于AR模型, 可有效提高洪水预报精度。文献[17]构建了基于LSTM的区域化洪水预报模型, 模型能够较好地模拟实际洪水过程。文献[18]引入LSTM网络建立山区中小流域降雨径流模型, 结果表明LSTM网络对山区中小流域暴雨洪水非线性关系具有良好的拟合效果。总体而言, LSTM网络或耦合LSTM的相关模型在降雨径流和洪水预报方面表现突出, 但该类模型在山区中小河流源头流域的洪水预报应用研究相对不多。为此本文构建崇阳溪上游流域LSTM洪水预报模型, 为防洪工作服务。
HTML
-
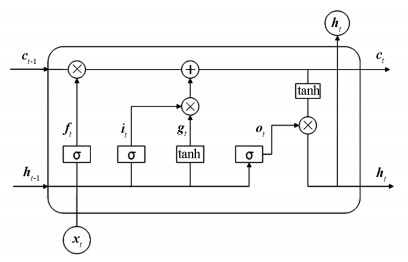
LSTM单元结构如图 1所示, xt为输入, LSTM单元包括遗忘门、输入门和输出门。
遗忘门为:
式中: ft为t时刻遗忘门输出向量;σ(·)为sigmoid激活函数;ht-1为t-1时刻的隐藏状态;Wxf、Whf为xt和ht-1对应的遗忘门权值矩阵;bf为遗忘门的偏置矩阵。
输入门为:
其中:it为t时刻输入门输出向量;tanh(·)为双曲正切激活函数;Wxi、Whi为xt和ht-1对应的输入门权值矩阵;bi为输入门的偏置矩阵;gt为t时刻的单元状态候选向量;Wxg、Whg为xt和ht-1对应的tanh层权值矩阵;bg为tanh层的偏置矩阵。
单元状态
式中:ct、ct-1分别为t、t-1时刻的单元状态更新向量。
输出门为:
其中:ot为t时刻输出门输出向量;Wxo、Who为xt和 ht-1对应的输出门权值矩阵;bo为输出门的偏置矩阵;ht为t时刻的隐藏状态。
-
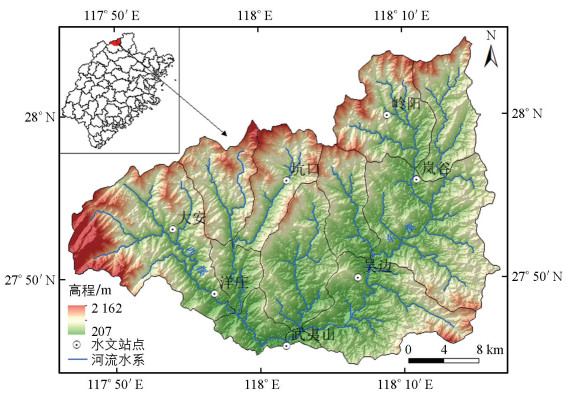
选取崇阳溪上游流域为研究区域(图 2)。该流域位于福建省武夷山市, 属于建溪支流崇阳溪的源头。武夷山水文站控制流域面积为1 078 km2, 包括东溪和西溪两条支流, 流经地形多为山地丘陵, 地势坡降大, 属于典型的山区流域。雨季期间, 暴雨频发容易导致洪水灾害。
-
收集了该流域1997年至2022年间30场暴雨洪水, 对其发生过程进行分析并建模, 其中训练集包括21场洪水、测试集包括9场洪水。在划分训练样本和测试样本的过程中, 均综合考虑了高、中、低不同量级的洪水过程以及不同峰型(如单峰、双峰)的洪水, 且样本数据具有代表性、可靠性、一致性、普遍适用性。测试集的9场洪水基本情况见表 1。
-
根据LSTM网络对时间序列的记忆能力, 在模型数据输入之前需要将不同序列数据在时间尺度下进行统一, 采用式(7)计算:
式中:Xi(t)为t时刻第i个雨量站降雨过程Pi对应的模型输入数据;τi为其净雨到武夷山站的汇流时间。综合分析确定洋庄、吴边、大安、坑口、岭阳、岚谷各雨量站净雨到武夷山站的汇流时间分别为1h、1.5 h、2.5 h、3 h、4 h、3 h。调整后的数据序列统一到同一个时间尺度下, 以满足LSTM模型的输入要求。
-
模型输入数据包括流量和雨量两种类型, 其来源和量纲不同, 数据值域相差较大。为了适应LSTM网络的学习, 论文采用(8)式所示Z-score标准化算法对数据进行标准化处理。
式中:z为标准化处理后的数据;x为标准化处理前的数据;μ为均值;σ为标准差。经过处理后数据的均值为0, 标准差为1, 值域为[-1, 1], 以此构建向量输入LSTM网络模型。在LSTM网络模型训练结束后, 对输出的预测结果再经过反标准化处理得到实际的输出预测值。
-
为衡量各雨量站的雨量在产汇流过程中的占比, 需要对该流域进行单元划分, 计算各控制站点子流域单元面积权重。根据泰森多边形法将流域划分为7个子单元, 各单元面积和权重占比见表 2。
-
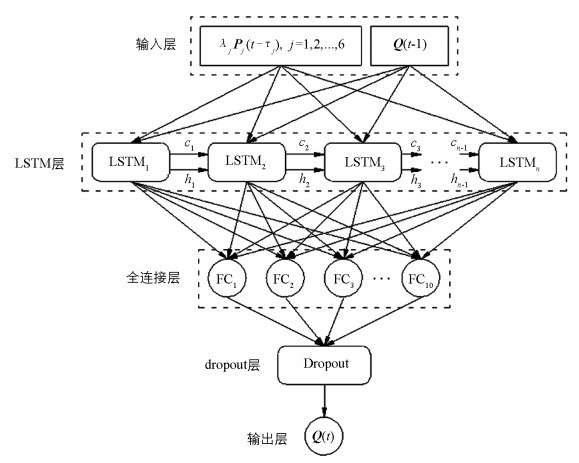
以崇阳溪上游6个雨量站的时段雨量数据为基础、增加流域控制断面武夷山水文站前1 h的流量数据作为模型输入, 以该站对应流量数据为预测目标, 建立山区流域LSTM神经网络洪水预报模型。网络模型结构如图 3所示。
输入层计算式为:
式中:a、b为去零化参数, 取a=0.5、b=2;λj为各雨量站子流域单元面积权重;μpj、σpj分别为输入的各雨量站时段雨量序列均值、标准差;μq、σq分别为武夷山水文站实测流量序列均值、标准差。t时刻模型输入层的输入包括:同步后的6个雨量站时段雨量Pj(t-τj);前1 h武夷山水文站记录的实测流量Q(t-1), 经该层预处理后转化为LSTM层的输入信息矩阵X(t)。
LSTM层计算式为:
t时刻LSTM层的输入包括:t-1时刻记忆单元输出的武夷山站流量信息矩阵h(t-1);t-1时刻记忆单元根据输入信息学习到的状态变量矩阵c(t-1);当前输入信息矩阵X(t)。经过输入门、遗忘门、输出门的激活函数运算, 舍弃使损失函数增大的负面信息, 记录对预测精度有正反馈的信息并更新单元状态, 以此生成当前流域出口断面流量信息矩阵h(t)。
在LSTM层之后设置了一个包含10个单元的全连接层, 用于将LSTM层各单元训练学习得到的数据特征进行整合, 以达到最终需要输出维度为1的结果。全连接层计算式为:
式中:yi(t)为全连接层各单元输出信息, 由LSTM层各单元输出的武夷山站流量信息矩阵h(k)整合而来;n为LSTM层单元数;Wyk、byk为全连接层的权值矩阵和偏置值。
在网络隐含层和输出层之间的全连接层进行dropout处理, 抛弃因子设置为10%, 该设置会在训练期间将全连接层10%的随机单元输出设置为零, 以便网络进行更稳健的特征学习, 从而增强模型的泛化能力并降低网络过拟合风险。dropout层计算式为:
式中:Y(t)为dropout层输出信息, 由全连接层各单元输出信息整合而来, dropout层使用了由0和1组成的10×1随机数矩阵以抛弃冗余信息。
在t时刻, 经全连接层整合、dropout层随机数筛选后再由输出层去标准化, 最终获得预测流量值。输出层计算式为:
式中:Q(t)为武夷山站预测流量值;μq、σq含义同式(9)。
-
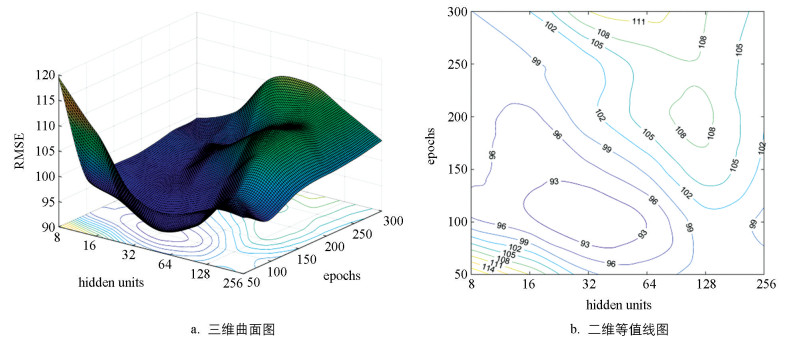
通过分析训练集洪水流量均方根误差(RMSE)平均值随LSTM层隐含层单元数和网络迭代轮数组合变化而变化的情况, 以此判定两个参数的最优组合。模型学习速度取0.01。表 3为模型训练结束后, 训练集洪水的RMSE平均值随LSTM层隐含层单元数(hidden units)和网络迭代轮数(epochs)组合变化的趋势, 并绘制其三维曲面、二维等值线图, 详见图 4所示。
根据表 2和图 4可见, 当LSTM层隐含层单元数为8、网络迭代轮数为50次时, RMSE值较大, 网络由于参数迭代不足而未收敛;随着两个参数的增加, RMSE值逐步降低, 当隐含层单元数为32、迭代轮数为100次时, RMSE达到最小;随着两个参数继续增大, RMSE值又开始上升。整体趋势面图像呈现出两端高、中间低的“山谷”形态。故最终确定LSTM隐含层单元数为32、网络迭代轮数为100。
根据选定的LSTM隐含层单元数和网络迭代轮数设置模型结构。在多次试算并反复调整参数后, 损失函数变化曲线趋于平稳, 网络训练结束, 至此完成LSTM神经网络洪水预报模型的构建。
-
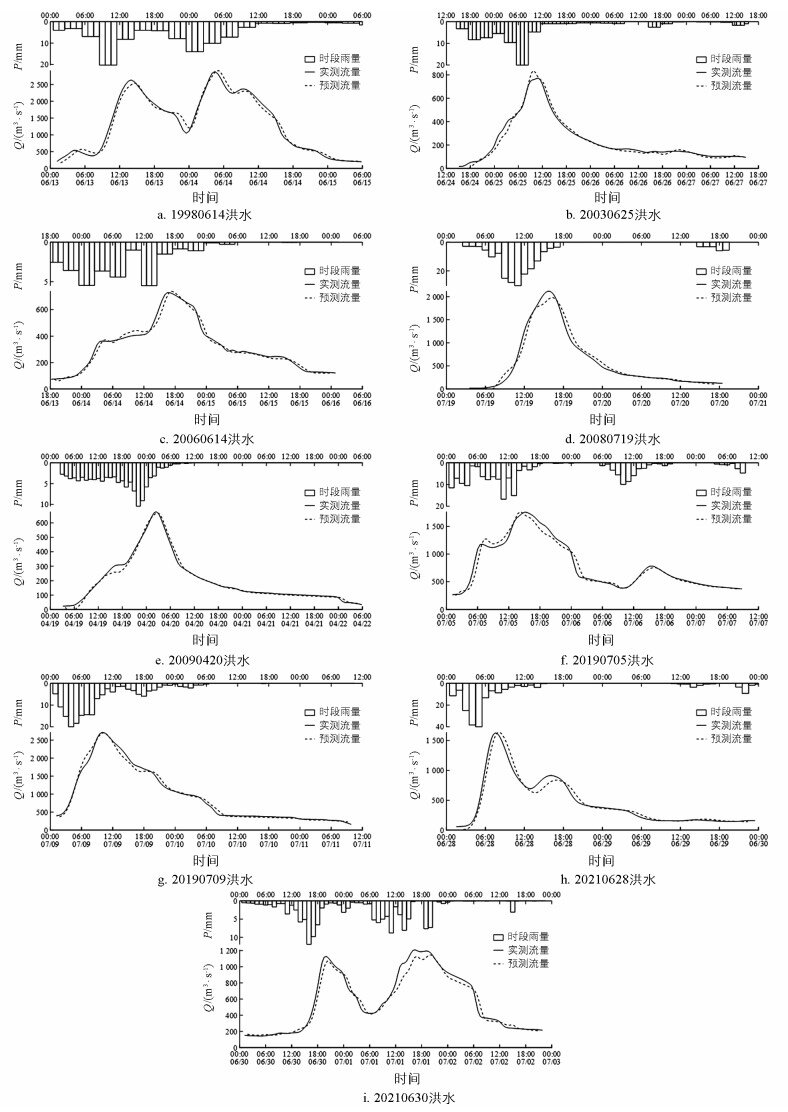
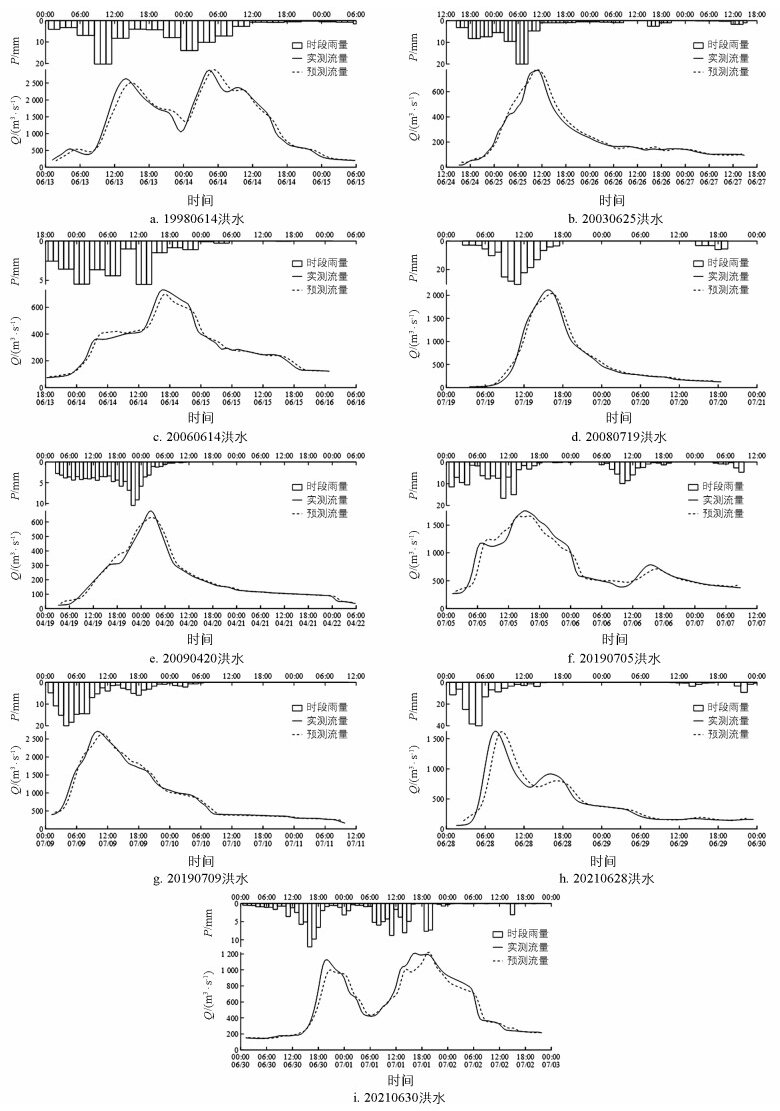
采用上述模型对选定的测试集9场暴雨洪水过程进行模拟验证, 得到9场洪水流量预报过程线图(图 5)。为了进行对比, 同样采用训练集样本构建流域LMBP神经网络洪水预报模型, 调试后的模型结构为7-8-1, 即输入层单元数为7、隐含层单元数为8、输出层单元数为1, 对选定的测试集9场暴雨洪水过程进行模拟, 结果见图 6。
采用绝对误差绝对值的平均值(取完绝对值后再平均, 下同)、相对误差绝对值的平均值、纳什效率系数3个评定指标对两个模型精度进行综合分析, 得到每场洪水流量过程预报误差见表 4, 洪峰流量相对误差和洪峰出现时间误差见表 5。其中相差时间是指洪峰出现预测时间减去实际出现时间。
综合LSTM模型整个预报过程线来看, 除20080719洪水过程平均相对误差为10.4%外, 其他误差均小于10%, 模型确定性系数均大于0.920。与LMBP模型的结果比较, 9场洪水流量预报过程中, 有8场洪水相对误差的平均值小于LMBP模型的误差, 7场洪水的确定性系数大于后者的确定性系数。
洪峰流量方面, 9场洪水的洪峰流量绝对误差总体较小, 平均值为58.6 m3/s, 误差最大值出现在19980614洪水主峰, 误差为175 m3/s, 高流量洪水的绝对误差大于中低流量洪水。9场洪水的洪峰流量相对误差都处在较为理想的范围, 平均值仅为3.7%, 误差最大值出现在20030625洪水主峰, 误差6.9%。LSTM模型在洪峰流量预测方面也相对占优, 误差较小, 精度略高于LMBP模型。
洪峰出现时间方面, 9场洪水洪峰出现时间误差最大值为1 h, 最小值为0, 平均时间误差为23 min, 处于允许的时差范围。每场洪水预测洪峰出现时间相较实测值或早或晚, 但总体上偏晚居多。与LMBP模型相比, LSTM模型在洪峰出现时间预测方面性能更好, 精度更高。
总体而言, 两种模型的精度均符合规范要求, 相对来说深度学习LSTM模型具有显著优势。
2.1. 流域概况
2.2. 样本数据处理
2.2.1. 同步化处理
2.2.2. 标准化处理
2.2.3. 子流域单元划分
2.3. 模型构建
2.4. 模型参数率定
2.5. 模型验证
-
针对崇阳溪源头山区流域地形地貌复杂的特点, 选取流域暴雨洪水过程, 采用均方根误差最小准则优化率定网络的LSTM隐含层单元数和网络迭代轮数, 在LSTM层之后设置了一个包含10个单元的全连接层, 并对全连接层进行dropout处理, 建立崇阳溪上游山区流域LSTM神经网络洪水预报模型。该网络适合用于模拟序列中具有时间间隔和延迟的数据关系, 以此生成流域出口断面流量过程信息。同时构建了该流域的LMBP模型进行比较, 主要结论如下:
1) LSTM与LMBP模型的对比结果表明, 具有深度学习功能的LSTM模型预测精度较高, 其在洪水过程、洪峰流量和洪峰出现时间预测方面的精度高于人工神经网络LMBP模型, 模型的确定性系数也明显占有优势, 因此适用于山区源头流域的洪水预报。
2) 通过考虑雨量站净雨到控制断面的汇流时间, 将不同序列数据在时间尺度下进行同步化处理后作为模型的输入, 预报效果相对更好。
3) 在LSTM层之后设置全连接层并对全连接层进行dropout处理, 其在LSTM层隐含层单元数和网络迭代轮数的优化组合选择中具有较好的优势, 可以提高模型的泛化能力。






 DownLoad:
DownLoad: