-
开放科学(资源服务)标识码(OSID):

-
无人潜航器(Unmanned Underwater Vehicle,UUV)是一种能长时间在水下自主航行并进行海洋侦察探测、排除水雷、救生以及水下攻击等作业的器具或系统,其在航行过程中撞击礁石产生的冲击载荷可能会对其圆柱壳体结构以及内部结构中的重要零件和传感器造成损坏[1],进而导致UUV丧失水下作业能力,因此碰撞载荷的动力学分析是其产品系统可靠性设计的关键部分,研究水下圆柱壳体撞击目标的碰撞载荷影响因素以及对碰撞载荷进行预测至关重要。
在圆柱壳体受冲击载荷影响的研究中,鱼雷壳体入水的冲击载荷以及船舶碰撞是国内外的研究热点。程伟等[2]、刘思华等[3]和潘光等[4]考虑了不同弹头形状、入水初速以及入水角度对冲击载荷的影响,研究结果可为预测鱼雷撞击水面时的冲击载荷提供参考;李刚[5]和贺征等[6]基于LS-DYNA软件研究了装配式导弹在垂直入水时的载荷分布,结果表明除了头部受到大冲击外,弹体的连接处也容易产生应力集中。关于UUV入水冲击的垂直载荷国内也有相关研究,李文颉等[7]基于RANS方程的数值模拟方法测量了UUV尾部不同入水角度下的砰击载荷、速度和加速度变化,结果表明:垂直载荷会随着UUV倾角增加而减小,入水过程中UUV会产生反复加减速运动;Shi等[8]通过任意拉格朗日型数值算法(Arbitary-Langrange-Eulerian,ALE)模拟分析了UUV入水时不同头型、撞水速度和入水角下的冲击载荷,研究发现随着头部半球角度与撞水速度的增加,UUV结构所受到的冲击力也增加,且轴向冲击力与入水角度的平方呈正相关,径向冲击力与入水角度的平方呈负相关。关于船舶等壳体结构的研究,Song等[9]、Ye等[10]和周刘茜[11]利用LS-DYNA程序对船舶碰撞进行了参数化分析,运用了ALE-FSI方法与考虑水动力效应下的附加质量法,研究了船舶初始速度、质量、碰撞角度和吃水深度对碰撞响应的影响,结果表明:初始速度和质量越大,接触力、能量耗散以及船舶损伤越大;碰撞角度增大会导致接触力与船舶损伤减小;随着吃水深度的增加,FSI结果与CAM值之比呈线性增加,说明水下发生碰撞时流体的影响不可忽视。
针对壳体结构碰撞理论的研究,国内学者岳建军等[12]基于Hertz接触理论[13]构建了碰撞载荷和系统位移的关系,通过数值仿真方法,分析了不同几何形状及约束条件的弹性薄板在冲击过程中表现出的瞬态动力学特征,讨论了冲击体曲率半径、初始动能及质量等关键参数对冲击载荷和载荷持续时间的影响规律;马子恒[1]采用Lankarani-Nikravesh接触力模型耦合双向流固耦合算法,对碰撞振动问题进行了理论研究,对比讨论了鱼雷的初始速度、质量、材料刚度以及头部橡胶的硬度对碰撞载荷的影响;Xu[14]将圆柱壳体视为一根弹性杆做简化计算,利用霍普金森杆进行碰撞环境下的加速度校准实验,并结合仿真方法分析了壳体头部几何形状对加速度波形的影响。
国外学者针对壳体结构碰撞动力响应也展开了相关研究,May[15]研究了入水角度对鱼雷壳体表面所受冲击载荷的影响;Her等[16]考虑了圆柱壳和球壳2种壳体结构,依托LS-DYNA软件完成了复合材料结构的冲击仿真,结果表明:壳体的曲率越小、边界条件越紧的结构刚度越大,接触力也就越大,变形挠度越小,且结构的冲击响应与冲击速度成正比;Khalili等[17]基于ABAQUS平台开展了壳体碰撞动力学数值模拟研究,通过参数化研究揭示了单元类型、网格尺寸及材料本构模型对碰撞力计算精度的影响。
综上所述,目前针对船舶等壳体结构在水中碰撞以及鱼雷入水冲击的相关研究较多,但对UUV等圆柱壳体结构在水下发生碰撞以及碰撞载荷预测的研究相对较少。因此,首先通过对比理论与仿真模型的计算结果验证理论模型的准确性和可靠性,再对封闭圆柱壳体在水中的碰撞进行数值模拟,讨论不同初始速度、碰撞质量、碰撞角度3因素对有水环境下碰撞载荷的影响,同时还考虑不同的水深对碰撞载荷的影响;然后对圆柱壳体在空气中的碰撞进行仿真分析,选取与水中相同的工况,讨论不同介质下封闭圆柱壳体在不同工况下的碰撞载荷;最后针对水下的研究结果,采用二次回归正交旋转中心组合方法,在固定水深10 m处,选取初始速度、碰撞质量和碰撞角度作为UUV系统设计的关键因素,获得碰撞载荷随3因素变化的近似预测模型,以期为UUV系统的可靠性设计提供必要性参考。
HTML
-
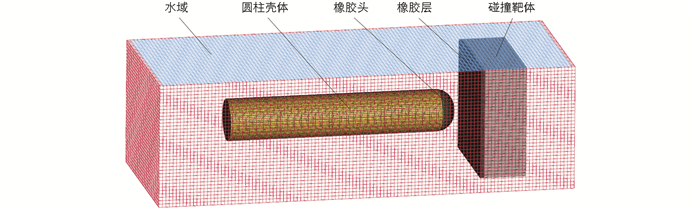
圆柱壳体碰撞的有限元模型如图 1所示,根据UUV圆柱壳体的实际结构,在建模过程中对其结构做简化处理,主要包括截头圆柱壳体、橡胶头等部分。由于圆柱壳体在空气中的碰撞属于低速碰撞,且空气密度很小,对圆柱壳体的阻尼也会很小,空气域对撞击结果的影响可以忽略不计[1],因此不设置空气域从而提高计算效率。只需要在UUV和靶体模型的周围建立尺寸为3 000 mm× 900 mm× 1 200 mm的流体域,流固耦合计算采用LS-DYNA中的ALE算法,该算法可以在求解过程中调整水域网格单元的空间位置,能有效处理大变形问题。同时碰撞靶体与UUV碰撞的面有厚度为30 mm的橡胶层。
在前处理时,固体与流体网格均采用八节点一阶六面体单元,空间上对橡胶层和碰撞靶体在撞击方向上的左端面、右端面、上端面和下端面完全约束(*SPC_SET),并且碰撞过程中采用自动面到面的接触(*AUTOMATIC_SURFACE_TO_SURFACE)。将圆柱壳体、橡胶层以及碰撞靶体的拉格朗日实体单元与ALE水域流体单元通过流固耦合法进行耦合计算(*CONSTRAINED_LANGRANGE_IN_SOLID)。对水域除顶面以外的5个面提取1层单元并设置为远场边界,再对5个面设置非反射边界条件(*NON_REFLECTING)。在考虑不同的水深对碰撞载荷的影响时,还需要对水域进行水体压力初始化(*ALE_AMBIENT_HYDROSTATIC和*INITIAL_HYDROSTATIC_ALE)。
-
1) 圆柱壳体材料使用7075铝合金,碰撞靶体材料使用Q235钢,均采用JOHNSON_COOK本构模型,其本构方程为:
式中:σy为屈服应力;A、B、C、n和m分别为与材料强度相关的常数;ε为等效塑性应变;
$ \dot{\varepsilon}^*$ 为归一化的等效塑性应变率;Tm=(T-Troom)/(Tmelt-Troom)为相对温度,其中T为变形温度,Troom为参考室内温度,Tmelt为使用材料的熔点。7075铝合金与Q235钢的JC本构材料参数[18-19]如表 1所示。2) 圆柱壳体橡胶头以及碰撞靶体橡胶层采用MOONEY_RIVILIN本构[20]进行描述,该材料模型适用广泛,可用于描述橡胶材料的力学行为,MOONEY_RIVILIN本构方程为:
式中:W为储能函数;C10和C01分别为与材料硬度相关的参数;I1和I2分别为应变张量的第1和第2不变量。
本次模拟计算中,橡胶密度ρ=1 350 kg/m3,泊松比υ=0.499,弹性模型E=17.33 N/m2,C10=2.972 MPa,C01=-0.082 MPa。
3) 水域与空气的材料采用*MAT_NULL空材料定义,参数来自文献[19],采用*EOS_GRUNEISEN状态方程模拟水的运动,其公式为:
其中:p1为水的压力;E1为水的初始内能;C为水中声速;γ0为Gruneisen常数;a为γ0的一次体积修正系数;S1~S3为状态方程系数;μ1由水的相对体积V1求得。本次计算中,水的密度ρ0=998.21 kg/m3,E1=2.533×105 Pa,C=1 647 m/s,S1=1.921,S2=-0.096,S3=0,γ0=0.35,V1=1。
空气的状态方程选用多线性状态方程*EOS_LINEAR_POLYNOMIAL,其公式为:
其中:C0~C6均为多项式方程的系数;E2为空气的初始内能;μ2由空气的相对体积V2求得。本次计算取空气密度为1.185 kg/m3,E2=2.533×105 Pa,C0=C1=C2=C3=0,C4=C5=0.4,C6=0,V2=1。
1.1. 模型建立
1.2. 材料选择
-
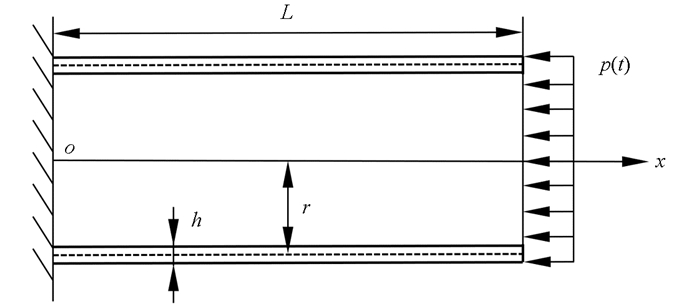
将碰撞问题简化为轴对称冲击载荷作用下的壳体动态响应模型,如图 2所示,基于Donnell壳体理论构建轴对称变形控制方程:
式中:x、y、z分别为轴向、周向和径向坐标;t为时间变量;Ui,tt(i=x,y,z)为各方向上的位移对时间的二阶导数,即加速度;Uz,x为径向位移对轴向坐标x的一阶偏导数;R、h、ρ分别为壳体的中面曲率半径、厚度及质量密度;Nxi,x(i=x,y)为轴向或剪切薄膜力对轴向坐标x的一阶偏导数;Mxx,x为弯矩Mxx对轴向坐标x的一阶偏导数;Ux、Uy、Uz分别为壳体中性曲面在各方向上的位移。
圆柱壳体中性曲面的薄膜力(壳体截面上单位长度的法向力与剪力)与弯矩(由应力分布不对称产生的弯曲与扭转效应)服从以下平衡方程:
式中:σij为柯西应力张量。
基于Donnell壳体理论,壳结构的轴对称变形运动学控制方程可表述为:
式中:εij为应变分量,ij=xx,xy,yy。
基于图 2所示的结构构型,圆柱壳体轴压冲击动力学响应的数学建模需满足以下约束体系:
壳体双端固支约束体系需满足:
式中:p(t)为轴向动态载荷的时变函数。
上述模型严格满足小应变理论框架,适用于有限变形范畴内的弹性材料响应分析。
-
基于连续介质力学框架,弹塑性动态响应的应变率张量
$ \dot{\varepsilon}_{i j}$ 可解耦为弹性应变率$ \dot{\varepsilon}_{i j}^{\prime}$ (可逆,服从广义胡克定律)与塑性应变率$ \dot{\varepsilon}_{i j}^{\prime \prime}$ (不可逆,由J2流动法则确定)分量,即:弹性应变率张量
$ \dot{\varepsilon}_{i j}^{\prime}$ 的本构关系可由广义胡克定律给出:式中:E、μ和δk分别为杨氏模量、泊松比和Kronecker Delta符号;σmm为应力球张量(静水压力分量)。
基于Drucker稳定性公设,塑性流动法则可导出为:
基于J2流动理论,各向同性硬化材料的加载函数f由修正的Von Mises准则定义,即:
式中:J2为偏应力第二不变量;k为各向同性硬化系数。基于J2流动理论框架,在各向同性硬化材料中G可表示为J2的函数,即:
基于Ramberg-Osgood本构关系的切线模量Et求解体系可表述为:
式中:n为控制塑性流动速率的硬化指数;Fs为当前应变对应的割线模量等效应力;σ为等效应力。
基于连续介质力学框架,结合式(12)-式(16),轴对称薄壳结构的本构关系可表述为如下对称张量方程:
式中:系数fij=cij-1,(i,j=1,2,3),且有:
基于非线性动力学系统的时程分析需求,采用增量式数值求解框架处理瞬态响应问题。针对材料非线性、几何大变形及接触边界的多重非线性耦合特性,通过时间离散化策略将连续动力学控制方程转化为逐步递推的代数方程组,即:
式中:εij(l)、σij(l)、Ui(l)、Mij(l)、Nij(l)分别为在t=t(l)=lΔt时不同物理量所对应的数值;Δεij(l)、Δσij(l)、ΔUi(l)、ΔMij(l)、ΔNij(l)分别为t(l)≤t≤t(l+1)时间内各物理量的增量函数。该解法通过将连续微分方程转化为离散差分方程,可以有效处理应力应变增量关系的时域演化问题。
根据式(7)可推导运动方程的增量形式,即:
将式(18)、式(19)的应力应变增量关系式代入式(8),即可求得ΔNxx(l)、ΔNyy(l)、ΔNxy(l)、ΔMxx(l)为:
其中,
基于对称性分析,参数A13、A23、B13恒为0,式(21)第2式中因几何对称性自动成立,核心目标聚焦于联立求解剩余的2个主导方程。
由式(10)和式(11)可知,初始条件和边界条件可由唯一增量来表示,分别为:
基于式(24)和式(25),将式(22)的内力和内力矩的增量形式代入式(21)的第1、3式,即可得到关于位移增量ΔUx、ΔUz的偏微分方程。通过离散化处理将偏微分方程转化为代数方程组,采用四阶Runge-Kutta法进行时程积分,结合中心差分格式实现空间离散,最终构建MATLAB数值计算框架从而求解关于ΔUx、ΔUz的运动控制方程,具体步骤如下:
步骤1 将圆柱壳体沿x和z方向进行网格划分,得到1组网格节点坐标。
步骤2 采用式(21),得到关于位移增量ΔUi(i=x,z)的二阶常微分方程组,采用Runge-Kutta法对时间积分,将二阶常微分方程转化为一阶常微分方程。
步骤3 将初始条件和边值条件用有限差分法的形式表示。
步骤4 令式(24)中的l=0,则在时间t(l)≤t≤t(l+1)的初边值问题可由Runge-Kutta法求解式(21),得到位移增量和速度增量ΔUi(0)、ΔUi,t(0)(i=x,z)。
步骤5 将所求的位移增量代入式(9)的增量形式可求初应变增量,再把应变增量代入式(18)可求得圆柱壳体上各点应力增量Δσij(0)(ij=xx,xy,yy)。
步骤6 将位移增量与应力增量代入式(20),求得相应节点的位移值和应力值Ui(l),σij(l)。
步骤7 利用式(19),在新的时间增量步内,计算各网格节点处新的应力应变系数fij,把fij代入式(23)中得到圆柱壳体上各点的Aij、Bij、Dij(i,j=1,2,3)值。
步骤8 令式(20)中的l=1,对于上一步获得的Aij、Bij、Dij值代入式(18)中,继续应用Runge-Kutta法求解。
步骤9 重复上述步骤,直至达到所期望的求解时间。
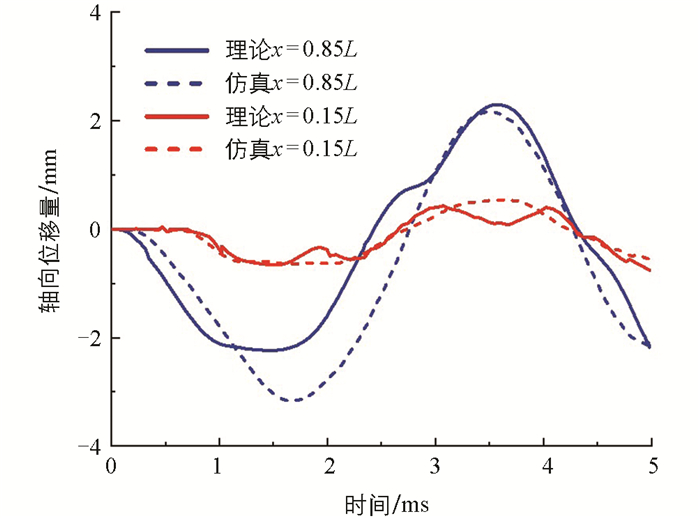
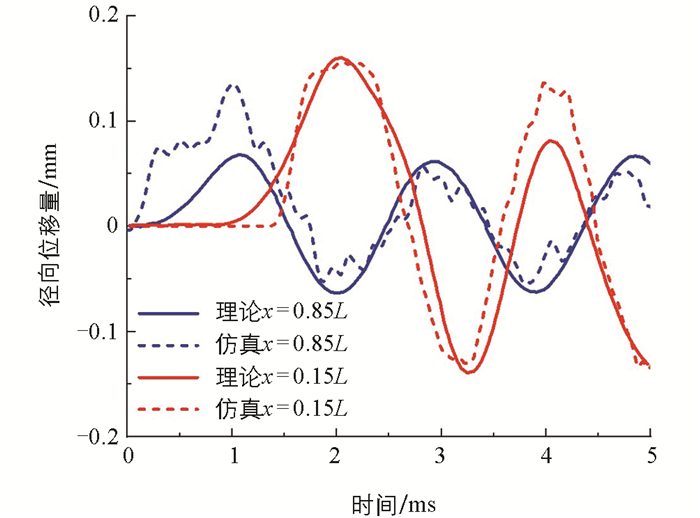
为了验证力学理论模型的准确性与可靠性,将圆柱壳体模型仿真结果与理论计算结果进行对比。圆柱壳体参数如下:h=10 mm,R/h=30,L/R=5.421,Fs=525 MPa。固定圆柱壳体底端对头部施加一个峰值为300 MPa、持续时间为2 ms的三角形载荷,通过理论与仿真计算得到圆柱壳体固定端(x=0.15L)与非固定端(x=0.85L)2处的无因次轴向位移与径向位移,分别如图 3和图 4所示。
由图 3可以看出,理论与仿真结果在变形初始阶段,非固定端的轴向位移增长速度比固定端更快,且理论轴向位移在1.52 ms左右达到最大值,仿真轴向位移在1.65 ms左右达到最大值,最大值相差较大(29.4%),这可以归因于仿真模型头部还存在半球头结构,随着时间增长均开始衰减振动,在随后的振动中两者出现的峰值仅相差6.4%。
由图 4可以看出,理论与仿真结果中非固定端径向位移的增长也较固定端更快,理论值在1.07 ms左右达到峰值,仿真值在1.01 ms左右达到峰值,随后开始衰减振动,初始两者峰值相差较大的原因可以归因于结构简化。随后固定端径向位移开始增长,理论值在2.06 ms左右达到峰值,仿真值在2.14 ms左右达到峰值,峰值相差2.6%,且两者峰值均比非固定端峰值大,随后开始衰减并在其平衡位置振动。总体而言,通过理论与仿真数据比较,验证了力学理论模型的准确性和可靠性。
2.1. 圆柱壳体运动方程
2.2. 增量数值解法
-
为了对比分析水中不同工况下的碰撞载荷,分别选取了不同的初始速度、碰撞质量、碰撞角度以及水的深度进行单因素影响分析,针对前3个单因素影响下的碰撞载荷与空气中的结果展开了详细的分析与讨论。
-
为了对比分析水中与空气中不同初始速度下的碰撞结果,设置仅初始速度不同的4种工况,分别为20 m/s、25 m/s、30 m/s、35 m/s,圆柱壳体的碰撞质量恒定为152.55 kg,碰撞角度恒定为0°,水深恒定为10 m。
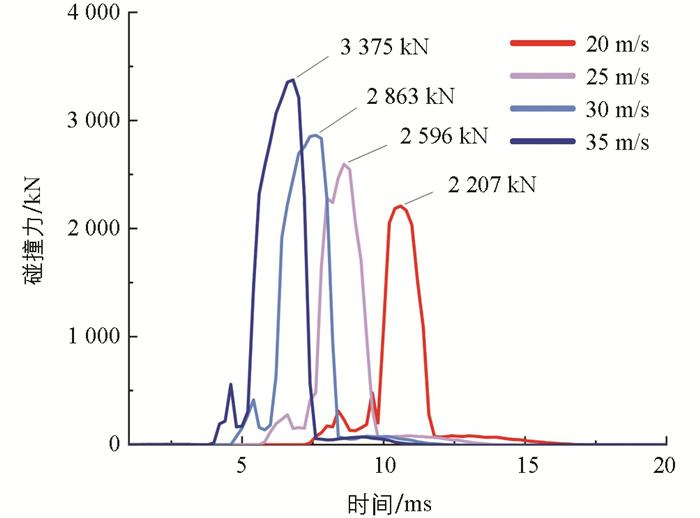
图 5给出了碰撞力的变化曲线,4种工况下的碰撞变化曲线近似呈正弦状,各曲线中的第1个正波峰产生的原因是圆柱壳体首先与橡胶层发生碰撞,达到1个较小的峰值后又与撞击体发生碰撞产生第2个数值较大的峰值。当速度逐渐增加时,碰撞力产生的时间也随之提前,且碰撞力分别在10.6 ms、8.6 ms、7.6 ms和6.8 ms时达到峰值2 207 kN、2 596 kN、2 863 kN和3 375 kN。
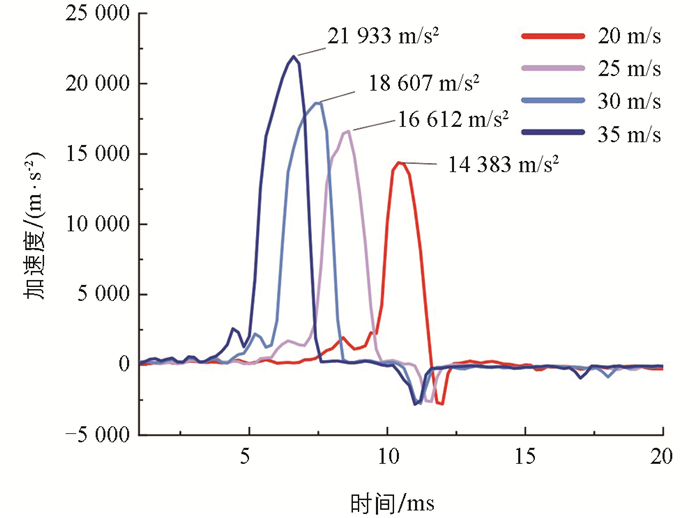
图 6给出了沿撞击方向的加速度分量变化曲线,4种工况下的加速度变化曲线也近似呈正弦形状且均包含正负波峰。曲线上的正峰值是由于与撞击体碰撞而产生的,负峰值是在碰撞结束后圆柱壳体尾部的水流因惯性继续向前流动,对壳体产生推进作用而形成的。与碰撞力的变化曲线相似,随着速度的增加,加速度产生的时间在不断提前,并分别在10.4 ms、8.6 ms、7.4 ms和6.6 ms时达到峰值14 383 m/s2、16 612 m/s2、18 607 m/s2和21 933 m/s2,这与碰撞力达到峰值的时间大致相同。撞击结束后在水流的推动作用下产生负峰值,当速度增大时,沿撞击方向的加速度分量负峰值分别在11.0 ms、11.2 ms、11.6 ms和12.0 ms时达到最大值-2 806 m/s2、-2 752 m/s2、-2 610 m/s2和-2 786 m/s2,由于质量均相同,4种工况下的负峰值大小近似相等。随着初始速度的不断提高,圆柱壳体的初始动能也越大,对壳体结构的动力学响应影响也越大。
-
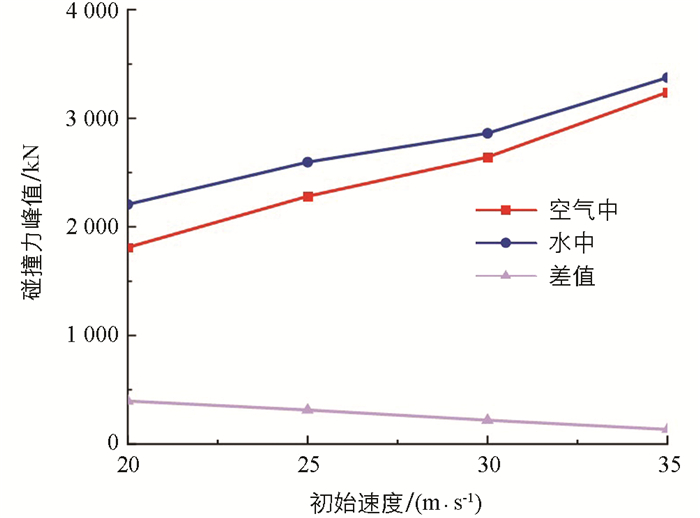
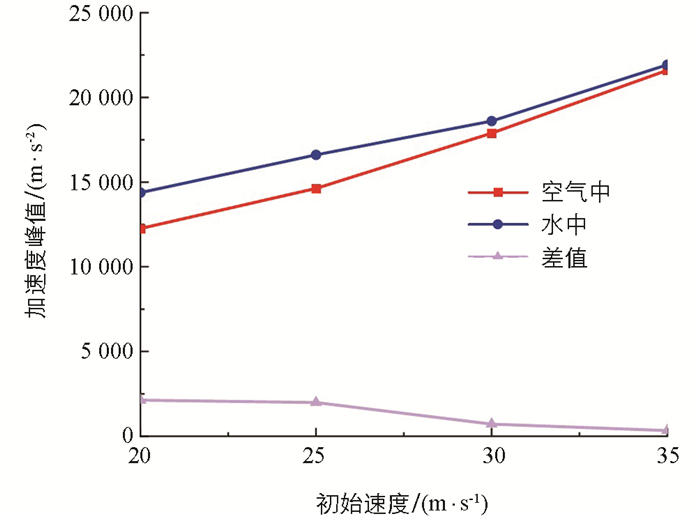
为了探究空气与水中各速度下碰撞力和沿撞击方向的加速度分量之间的关联,选取与水中相同的工况对圆柱壳体在空气中的碰撞进行了仿真分析,提取空气以及水中各速度工况下的碰撞力以及沿撞击方向的加速度分量峰值,如图 7和图 8所示。
由图 7可以看出,以相同速度发生碰撞时,在水中的碰撞力峰值比在空气中的更大,且随着速度的增加,加速度与碰撞力峰值的差值逐渐减小,这一规律满足水中运动物体的最小压力公式[21]:
式中:P0为水中运动物体上任一点的水压力;ξmax为物体表面的减压系数;ρ0为水的密度;ν为物体的运动速度。
由式(26)可以看出,当UUV的速度不断提高,壳体表面水压载荷持续衰减至临界空化压力时,就会产生空化效应[22]。当壳体在水中加速运动时,其运动轨迹周围的流体介质因黏性作用形成伴随运动的流场,这部分受迫运动流体产生的惯性阻力通过压力场作用于壳体表面,其作用效果等同于附加一定质量的虚拟流体层与壳体产生同步加速度响应[22]。因而当动水压力减小时,附加在圆柱壳体上的水的惯性力减小,导致碰撞力减小。
由图 8可以看出,水中与空气中沿撞击方向的加速度分量峰值变化规律与不同速度下的碰撞力峰值类似,在水中的加速度分量峰值均大于在空气中的加速度分量峰值。由于圆柱壳体在水中运动时受到静水压力以及动水压力的作用,使其在发生碰撞时的载荷增大,从而使圆柱壳体加速度分量峰值也增大。
-
为了对比分析水中与空气中不同碰撞质量下的碰撞结果,通过改变圆柱壳体内部结构密度,从而改变圆柱壳体整体质量,设置仅碰撞质量不同的4种工况,分别为152.55 kg、177.55 kg、202.55 kg、227.55 kg,圆柱壳体的初始速度恒定为25 m/s,碰撞角度恒定为0°,水深恒定为10 m。
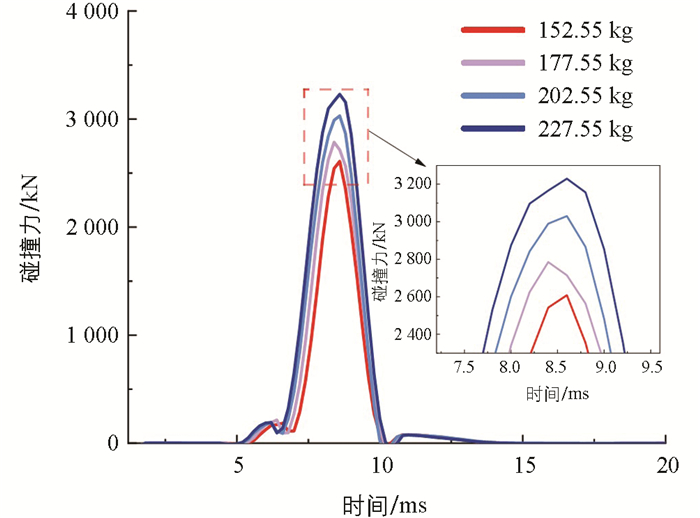
图 9给出了碰撞力的变化曲线,曲线形状近似呈正弦状,随着碰撞质量的不断提高,碰撞力产生的时间在不断提前,且碰撞力分别在8.6 ms、8.4 ms、8.6 ms和8.6 ms时达到峰值2 596 kN、2 664 kN、2 947 kN和3 265 kN,达到峰值的时间大致相同。碰撞质量越大,圆柱壳体的初始动能越大,发生碰撞时更多的动能转化成形变能,导致碰撞力增加。
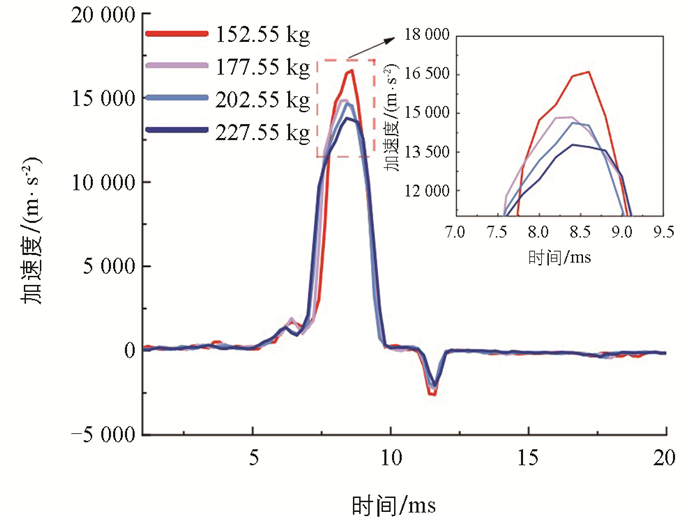
图 10给出了沿撞击方向的加速度分量变化曲线,当碰撞质量不断增大时,沿撞击方向的加速度分别在8.6 ms、8.4 ms、8.4 ms和8.4 ms时达到峰值16 612 m/s2、14 846 m/s2、14 633 m/s2和13 781 m/s2,这与碰撞力达到峰值的时间接近,且随着质量的增加峰值逐渐减小。撞击结束后由于水流的推动产生负峰值,当质量逐渐增大时,加速度负峰值均在11.6 ms时达到最大值-2 578 m/s2、-2 268 m/s2、-2 109 m/s2和-2 048 m/s2,负峰值的大小也随着质量的增加而不断减小。由此可见,当碰撞质量逐渐增大时,对圆柱壳体内部的加速度检测装置带来的影响逐渐减小。
-
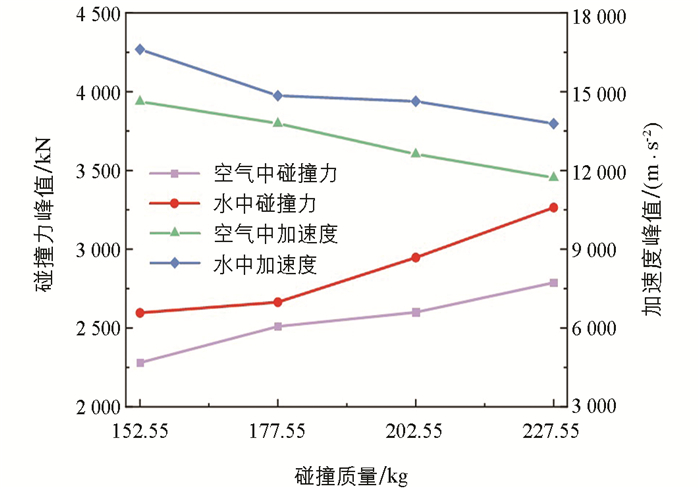
选取与水中相同的工况对圆柱壳体在空气中的碰撞进行仿真分析,并将空气与水中不同碰撞质量下的碰撞力峰值提取出来,不同介质中碰撞力和沿撞击方向的加速度分量峰值与碰撞质量的关系如图 11所示。由于圆柱壳体受到动水压力的作用,碰撞发生时动水压力等效于附着在壳体表面一定质量的水共同运动产生的惯性力,所以在不同碰撞质量下水中发生碰撞时的碰撞力峰值大于空气中的碰撞力峰值。在动水压力的作用下碰撞载荷增大,使得在水中碰撞时沿撞击方向的加速度分量峰值大于空气中的加速度分量峰值,且随着质量的增大,加速度分量峰值逐渐降低。
-
为了对比分析水中与空气中不同碰撞角度下的碰撞结果,设置仅碰撞角度不同的4种工况,分别为15°、30°、45°和60°,圆柱壳体的初始速度恒定为25 m/s,碰撞质量恒定为152.55 kg,水深恒定为10 m。
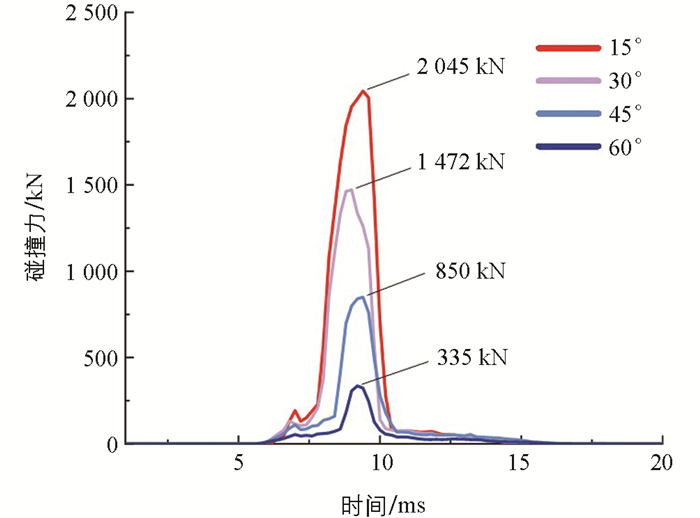
图 12给出了沿撞击方向的碰撞力变化曲线,随着碰撞角度的增加,碰撞力分别在9.4 ms、9.0 ms、9.4 ms和9.2 ms时达到峰值2 045 kN、1 472 kN、850 kN和335 kN,碰撞角度越小,撞击持续的时间也越长,圆柱壳体发生碰撞后,动能更多的转化成形变能,导致碰撞力的增加。
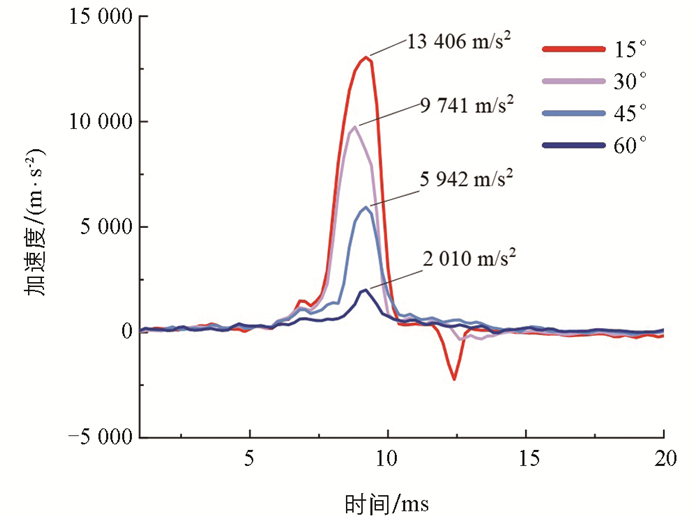
图 13给出了沿撞击方向的加速度分量变化曲线,随着碰撞角度的增大,碰撞结束后圆柱壳体沿碰撞方向的速度越大,水流的推进作用越不明显,所以沿撞击方向的加速度分量变化曲线上的负波峰逐渐减小直至消失。碰撞角度由15°增大至60°时,分别在9.2 ms、8.8 ms、9.2 ms和9.2 ms时达到加速度分量峰值13 406 m/s2、9 741 m/s2、5 942 m/s2和2 010 m/s2,这与碰撞力达到峰值的时间大致相同。当碰撞角度逐渐增大时,发生碰撞后侧向加速度分量增大,导致沿撞击方向的加速度分量峰值减小。
-
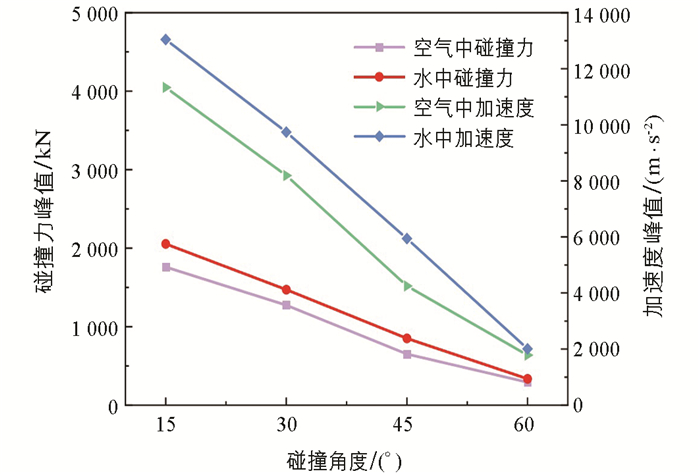
同样选取与水中相同的工况对圆柱壳体在空气中的碰撞进行仿真分析,将空气与水中不同碰撞角度下的碰撞力与沿撞击方向的加速度分量峰值提取出来,不同介质中沿撞击方向的碰撞力和加速度分量峰值与碰撞角度的关系如图 14所示。碰撞角度直接影响了初始速度沿撞击方向的分量大小,当碰撞角度增大时,沿撞击方向的速度逐渐减小导致圆柱壳体初始动能降低,使得2种介质下的碰撞力及加速度分量峰值降低,且水中发生碰撞时沿撞击方向的碰撞力与加速度分量峰值大于空气中的碰撞力与加速度分量峰值。
-
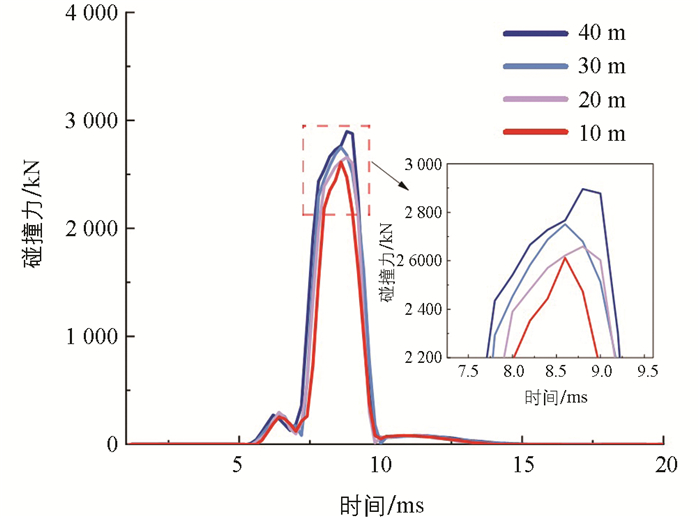
为了对比分析不同水的深度对碰撞载荷的影响,在不改变其他参数的情况下,仅设置水的深度分别为10 m、20 m、30 m和40 m共4种工况。图 15给出了碰撞力的变化曲线,当水的深度逐渐增加时,圆柱壳体在水中运动时所受的动水压力也在逐渐增大,与撞击体发生碰撞产生的碰撞力也逐渐增大,且碰撞力分别在8.6 ms、8.8 ms、8.6 ms和8.8 ms时达到峰值2 596 kN、2 674 kN、2 787 kN和2 910 kN。
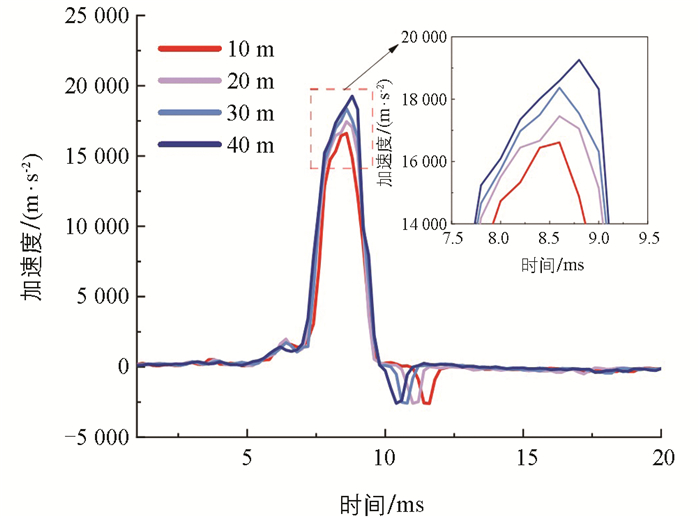
图 16给出了沿撞击方向的加速度分量变化曲线,4种工况下的加速度变化曲线近似呈正弦状,各曲线均存在正负波峰。随着水深的不断增加,4种工况下加速度产生的时间基本相同,并分别在8.6 ms、8.6 ms、8.6 ms和8.8 ms时达到正峰值16 612 m/s2、17 455 m/s2、18 370 m/s2和19 262 m/s2,这与碰撞力达到峰值的时间大致相同。撞击结束后在流体的推动作用下加速度变化曲线产生负波峰。当水深增加时,流体内部压力增大,使得撞击结束后在惯性作用下流体推动圆柱壳体尾部的时间提前,由于圆柱壳体质量均相同,4种工况下的负峰值大小近似相等,加速度负峰值分别在11.6 ms、11.0 ms、10.8 ms和10.4 ms时达到最大值-2 610 m/s2、-2 593 m/s2、-2 583 m/s2和-2 589 m/s2。
3.1. 初始速度对碰撞结果的影响
3.1.1. 不同初始速度下的碰撞结果
3.1.2. 空气与水中初始速度的影响分析
3.2. 碰撞质量对碰撞结果的影响
3.2.1. 不同碰撞质量下的碰撞结果
3.2.2. 空气与水中碰撞质量的影响分析
3.3. 碰撞角度对碰撞结果的影响
3.3.1. 不同碰撞角度下的碰撞结果
3.3.2. 空气与水中碰撞角度的影响分析
3.4. 不同水的深度对碰撞力和加速度的影响
-
在UUV进行水下作业的真实场景中,实际碰撞的碰撞参数存在多种组合方式,这就为UUV圆柱壳体撞击时的真实冲击载荷添加了不确定性,可能导致圆柱壳体结构损坏,从而使UUV丧失水下作业能力。通过二次回归正交旋转中心组合的方法,在水深固定的情况下,拟合沿撞击方向的碰撞力峰值Y1和加速度分量峰值Y2与圆柱壳体初始速度A、碰撞质量B以及碰撞角度C的关系。该方法是正交试验与回归分析相结合的一种设计方法,既保留了正交试验数据均匀分散的特点,还具备回归分析的预测功能,且多用于最优方案的选取以及最佳生产工艺的制定[23-25]。根据UUV与礁石的相对位置,实时预测UUV圆柱壳体即将受到的冲击载荷峰值大小,并根据冲击载荷的大小实时调整UUV航行速度与方向,避免发生因碰撞造成的结构损坏。
预测模型的初始速度取值范围为20~50 m/s;碰撞质量取值范围为152.55~252.55 kg;碰撞角度取值范围为0°~60°。根据3因素5水平二次回归正交旋转中心组合方法共计算了23组不同工况下的水下仿真数据,每组仿真重复3次,取平均值作为最终的仿真结果,如表 2所示。
应用Design-Expert 8.0.6软件对表 2中的数据进行分析,建立A、B和C 3因素回归模型,计算得到回归系数,则沿撞击方向的碰撞力峰值Y1和加速度分量峰值Y2的回归拟合方程分别如式(27)和式(28)所示:
对2个回归方程进行方差分析,如表 3所示。各仿真因素对碰撞力以及加速度分量峰值均具有极显著的影响,影响由大至小依次为碰撞角度、初始速度、碰撞质量。其中,初始速度与碰撞角度的交互作用对碰撞力峰值和加速度分量峰值有极显著的影响,碰撞质量与碰撞角度只对碰撞力峰值有显著影响。
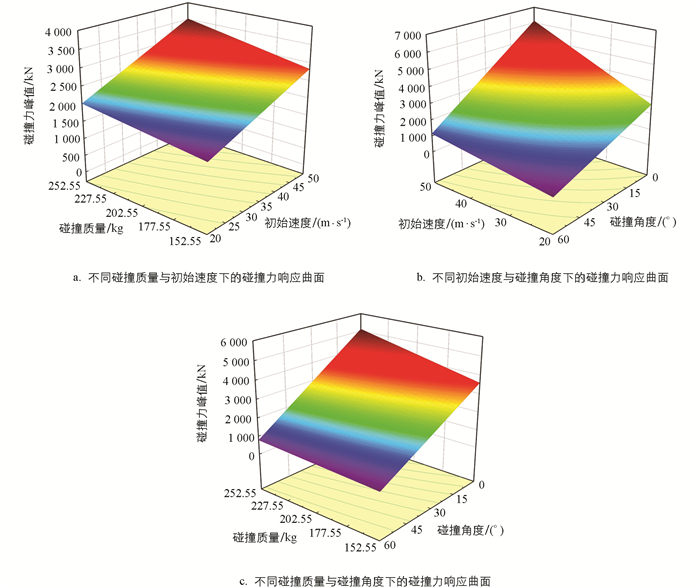
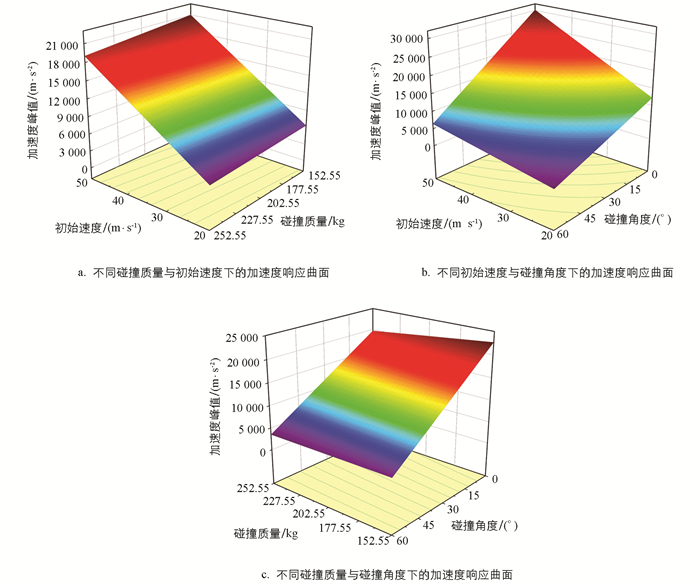
分别对上述回归方程绘制沿撞击方向的碰撞力峰值与加速度分量峰值的三维响应曲面图,如图 17、图 18所示。
当碰撞角度(30°)位于设计中心点时,初始速度和碰撞质量对碰撞力及加速度峰值的影响规律如图 17a和图 18a所示。由图可知,当初始速度增加时,会导致碰撞力及加速度峰值的增加;而碰撞质量增大时,会使碰撞力峰值增加但加速度逐渐减小。这是因为初始速度的大小会影响圆柱壳体的初始动能,初始动能越大,撞击过程中动能更多的转变为结构变形能,使得碰撞力以及加速度峰值增大;而碰撞质量的大小不仅与初始动能有关,还与加速度值的计算相关。由牛顿第二定律可知,质量与加速度呈负相关关系,所以碰撞质量增大,加速度峰值会逐渐降低。
当初始速度(35.0 m/s)位于设计中心点时,碰撞角度和碰撞质量对碰撞力及加速度峰值的影响规律如图 17b和图 18b所示。由图可知,碰撞质量的变化引起的碰撞力与加速度峰值的增减幅度没有碰撞角度引起的大。当碰撞质量增加时,会使碰撞力峰值的增加但加速度峰值逐渐减小;当碰撞角度增大时,碰撞力与加速度峰值下降幅度较大。
当碰撞质量(202.55 kg)位于设计中心点时,初始速度和碰撞角度对碰撞力及加速度峰值的影响规律如图 17c和图 18c所示。由图可知,随着初始速度的增大,碰撞力与加速度峰值的增加幅度较大;而碰撞角度直接影响了初始速度沿撞击方向的分量大小。当碰撞角度减小时,沿撞击方向的速度逐渐增大,导致碰撞力及加速度峰值的增加幅度较大。
-
为进一步验证二次回归模型的可靠性,任意选择3组不同工况的仿真方案进行验证,每组仿真重复3次,结果取平均值,最终的仿真结果如表 4所示。从仿真结果可以看出,随机选择的3组仿真方案的预测值结果误差在0.80%~4.11%之间,误差百分比较小,说明仿真结果与构建的预测模型具有较高的重复性,因此预测模型可靠。
4.1. 碰撞力与加速度峰值的预测模型构建
4.2. 验证仿真
-
利用有限元数值方法研究了UUV圆柱壳体在不同介质下以不同初始速度、碰撞质量和碰撞角度对碰撞载荷的影响以及不同水深下的动力学特性,并在一定取值范围内对前3个因素构建了近似预测模型,同时进行仿真验证,得到以下结论:
1) 圆柱壳体在水中发生碰撞时的碰撞力及加速度峰值均比在相同工况下的空气中要大,这是由于在水中运动时圆柱壳体表面受到了动水压力的作用,可以等效为附加在壳体上的一定质量的水伴随着圆柱壳体一起在水中运动产生的惯性力,使得碰撞时的载荷增大。水下碰撞时加速度会出现负峰值,这是由于在碰撞结束后圆柱壳体尾部的水流因惯性对壳体产生推进作用而形成的。随着水深的增加,碰撞载荷也会增大,说明UUV航行深度越大,所受到的载荷也将变大。
2) 2种介质中发生碰撞时的载荷变化规律大致相同。初始速度增大时,碰撞力以及加速度峰值也会随之增大,这是由于初始速度影响初始动能的大小,动能越大,撞击过程中动能更多地转变为结构变形能,使得碰撞力以及加速度峰值增大。随着碰撞质量的增大,圆柱壳体初始动能增加,由牛顿第二定律可知,质量与加速度呈负相关关系,因此碰撞质量增大,碰撞力峰值增大的同时加速度峰值会逐渐降低。当碰撞角度增大时,直接导致了沿撞击方向的速度分量降低,使得碰撞力以及加速度峰值减小。因此,UUV圆柱壳体在较大初始速度、较大质量、较小角度碰撞时,所受的载荷最大。
3) 采用3因素5水平二次回归正交旋转中心组合试验的方法,以初始速度、碰撞质量和碰撞角度作为UUV系统设计的评价指标,构建碰撞载荷随3因素变化的响应曲面以及数学回归方程,得到影响碰撞载荷的因素由高至低的顺序为:碰撞角度、初始速度、碰撞质量。通过仿真对回归方程的可靠性进行验证,结果表明拟合方程具有较高的重复性,不仅可以有效地预测碰撞时的载荷,还为UUV系统的可靠性设计提供了重要参考。






 DownLoad:
DownLoad: