Two Types of Nested Recursive Methods for Finding Counting Formulas of Perfect Matching Number

Bao-xiang TANG; Han REN

doi:10.13718/j.cnki.xsxb.2019.08.005

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

The perfect matching of graphs 2-nD₈ and 2-nD₆ has been classified according to the perfect matching of a certain vertex of saturation, and the recursive relation of each kind of perfect matching number been obtained. Then the interrelationship between these recursive formulas has been used to eliminate those that are not needed. The recursive relation has been used to obtain the recursive relation of the perfect matching number of the two kinds of graphs. Finally, the formula for calculating the perfect matching number of the two graphs has been solved from the recursive formula.

HTML

图的完美匹配计数理论在很多领域有广泛的应用，其中的计数思想和方法对组合数学产生了重要影响，因此受到众多学者的关注^[1-16].本文用嵌套递推方法给出了2类2-边连通图完美匹配数目的计算公式.

定义1  设图G是有完美匹配的图，若图G的两个完美匹配M₁和M₂中有一条边不同，则称M₁和M₂是G的两个不同的完美匹配.

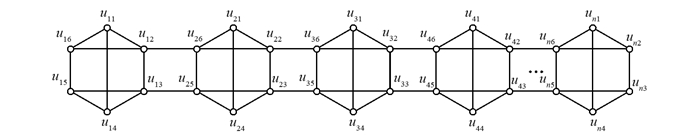
定义2  n个8圈为C₈ⁱ：u_i1u_i2u_i3u_i4u_i5u_i6u_i7u_i8u_i1.分别连接圈C₈ⁱ的顶点u_i1与u_i6，u_i2与u_i5，u_i3与u_i8，u_i4与u_i7(i=1，2，…，n)，再将圈C₈ⁱ和圈C₈ⁱ⁺¹顶点u_i3与u_i+1，8，u_i4与u_i+1，7分别连接起来(i=1，2，…，n－1)，这样得到的图记为2－nD₈，如图 1所示.

定义3  n个6圈为C₆ⁱ：u_i1u_i2u_i3u_i4u_i5u_i6v_i1.分别连接圈C₆ⁱ的顶点u_i1与u_i4，u_i2与u_i6，u_i3与u_i5(i=1，2，…，n)，再将圈C₆ⁱ和圈C₆ⁱ⁺¹顶点u_i2与u_i+1，6，u_i3与u_i+1，5分别连接起来(i=1，2，…，n－1)，这样得到的图记为2－nD₆，如图 2所示.

定理1  设图 2-nD₈的完美匹配数记为f(n)，则

证  易知图 2-nD₈有完美匹配.为了求函数f(n)的解析式，先定义图G₁，并求其完美匹配的数目.将路v₁v₂的端点v₁和v₂分别与图 2-nD₈的顶点u₁₈和u₁₇各连接一条边，所得到的图记为G₁，如图 3所示.

易知图G₁有完美匹配，设g(n)表示图G₁的完美匹配的数.

先求g(n)的表达式.设图G₁完美匹配的集合为M，G₁含边v₁v₂，v₁u₁₈的完美匹配集合分别为M₁，M₂，则M₁∩M₂=ϕ，M=M₁∪M₂，g(n)=|M|=|M₁|+|M₂|.

求|M₁|.因为v₁v₂∈M₁，所以v₁u₁₈，${v_2}{u_{17}} \notin {M_1}$.由f(n)的定义知，|M₁|=f(n).

求|M₂|.由g(n)的定义知，M₂中包含边v₁u₁₈，v₂u₁₇，u₁₁u₁₂，u₁₅u₁₆的完美匹配数为g(n－1)；

由g(n)的定义知，M₂中包含边v₁u₁₈，v₂u₁₇，u₁₁u₁₆，u₁₂u₁₅的完美匹配数为g(n－1)；

由f(n)的定义知，M₂中包含边v₁u₁₈，v₂u₁₇，u₁₁u₁₆，u₁₂u₁₃，u₁₄u₁₅的完美匹配数为f(n－1).

M₂中上述3类完美匹配互不包含，互不相交，且穷尽了M₂中所有完美匹配，故

综上所述，就有

再求f(n).设图 2-nD₈完美匹配的集合为M⁽¹⁾，图 2-nD₈含边u₁₁u₁₈，u₁₈u₁₃，u₁₈u₁₇的完美匹配集合分别为M₃，M₄，M₅，则M_i∩M_j=ϕ(3≤i＜j≤5)，M⁽¹⁾=M₃∪M₄∪M₅，f(n)=|M⁽¹⁾|=|M₃|+|M₄|+|M₅|.

求|M₃|.由f(n)的定义知，M₃中包含边u₁₁u₁₈，u₁₂u₁₃，u₁₄u₁₇，u₁₅u₁₆的完美匹配数为f(n－1)；

由g(n)的定义知，M₃中包含边u₁₁u₁₈，u₁₇u₁₆，u₁₂u₁₅的完美匹配数为g(n－1)；

由f(n)的定义知，M₃中包含边u₁₁u₁₈，u₁₇u₁₆，u₁₂u₁₃，u₁₄u₁₅的完美匹配数为f(n－1).

M₃中上述3类完美匹配互不包含，互不相交，且穷尽了M₃中所有完美匹配，故

求|M₄|.由f(n)的定义知，M₄中包含边u₁₁u₁₂，u₁₃u₁₈，u₁₆u₁₇，u₁₄u₁₅的完美匹配数为f(n－1)；

由f(n)的定义知，M₄中包含边u₁₃u₁₈，u₁₄u₁₇，u₁₁u₁₆，u₁₂u₁₅的完美匹配数为f(n－1)；

由f(n)的定义知，M₄中包含边u₁₃u₁₈，u₁₄u₁₇，u₁₁u₁₂，u₁₅u₁₆的完美匹配数为f(n－1).

M₄中上述3类完美匹配互不包含，互不相交，且穷尽了M₄中所有完美匹配，故

求|M₅|.由g(n)的定义知，M₅中包含边u₁₁u₁₂，u₁₅u₁₆，u₁₇u₁₈的完美匹配数为g(n－1)；

由g(n)的定义知，M₅中包含边u₁₇u₁₈，u₁₁u₁₆，u₁₂u₁₅的完美匹配数为g(n－1)；

由f(n)的定义知，M₅中包含边u₁₇u₁₈，u₁₁u₁₆，u₁₂u₁₃，u₁₄u₁₅的完美匹配数为f(n－1).

M₅中上述3类完美匹配互不包含，互不相交，且穷尽了M₅中所有完美匹配，故

综上所述，有

把(1)式代入(2)式，得

由(1)式，得

由(3)－(4)式，得

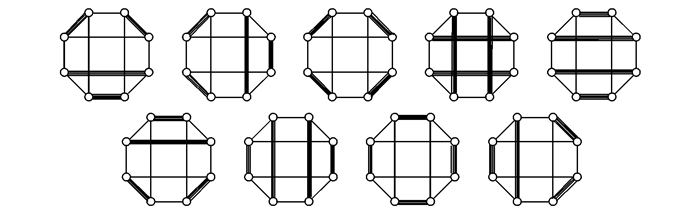
如图 4知，f(1)=9.

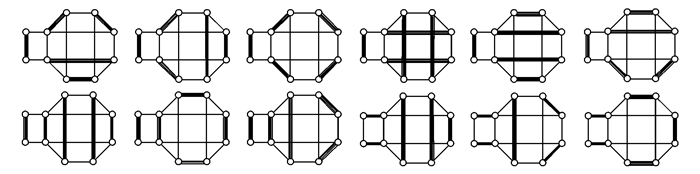
如图 5知，g(1)=12.

由(1)式，得

线性递推式(5)的特征方程为x²－11x+9=0，特征根为$x = \frac{{11 \pm \sqrt {85} }}{2}$.故(5)式的通解为

所以(5)式满足f(1)=9，f(2)=90的解为

定理2  设图 2-nD₆的完美匹配数记为σ(n)，则σ(n)=4·5^n－1.

证  易知图 2-nD₆有完美匹配.为了求函数σ(n)的解析式，先定义图G₄，并求其完美匹配的数目.将长为1的路v₁v₂的端点v₁和v₂分别与图 2-nD₆的顶点u₁₆和u₁₅各连接一条边，所得到的图记为G₄，如图 6所示.

易知图G₄有完美匹配，设τ(n)表示图G₄的完美匹配数.设图G₄完美匹配的集合为M⁽²⁾，G₄含边v₁v₂，v₁u₁₆的完美匹配集合分别为M₆，M₇，则M₆∩M₇=ϕ，M⁽²⁾=M₆∪M₇，τ(n)=|M⁽²⁾|=|M₆|+|M₇|.

求|M₆|.因为v₁v₂∈M₆，所以由σ(n)的定义知，|M₆|=σ(n).

求|M₇|.由τ(n)的定义知，M₇中包含边v₁u₁₆，v₂u₁₅，u₁₁u₁₄的完美匹配数为τ(n－1)；

由σ(n)的定义知，M₇中包含边v₁u₁₆，v₂u₁₅，u₁₁u₁₂，u₁₃u₁₄的完美匹配数为σ(n－1).

M₇中上述2类完美匹配互不包含，互不相交，且穷尽了M₇中所有完美匹配，故

综上所述，有

再求σ(n).设图 2-nD₆的完美匹配的集合为M⁽³⁾，图 2-nD₆含边u₁₁u₁₆，u₁₂u₁₆，u₁₅u₁₆的完美匹配集合分别为M₈，M₉，M₁₀，则M_i∩M_j=ϕ(8≤i＜j≤10)，M⁽³⁾=M₈∪M₉∪M₁₀，σ(n)=|M⁽³⁾|=|M₈|+|M₉|+|M₁₀|.

求|M₈|.因为u₁₁u₁₆，u₁₄u₁₅∈M₈，所以由τ(n)的定义知，|M₈|=τ(n－1).

求|M₉|.因为u₁₂u₁₆，u₁₃u₁₅，u₁₁u₁₄∈M₈，所以由σ(n)的定义知，|M₉|=σ(n－1).

求|M₁₀|.由τ(n)的定义知，M₁₀含边u₁₅u₁₆，u₁₁u₁₄的完美匹配数为τ(n－1)；

由σ(n)的定义知，M₁₀含边u₁₅u₁₆，u₁₁u₁₂，u₁₃u₁₄的完美匹配数为σ(n－1).

M₁₀中上述2类完美匹配互不包含，互不相交，且穷尽了M₁₀中所有完美匹配，故

综上所述，有

把(6)式代入(7)式，得

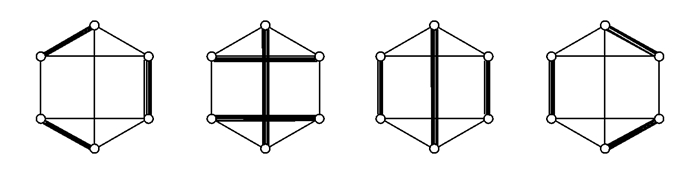
如图 7知，σ(1)=4.

故(8)式满足σ(1)=4的解为

Figure (7) Reference (16)

Name
	Name cannot be empty!
E-mail
	Mailbox cannot be empty! Mailbox cannot be empty!
Telephone
	Mobile number cannot be empty! Please enter a valid mobile number!
Title

Content
Verification Code

[1]	Valiant L G.The Complexity of Computing the Permanent[J]. Theoretical Compute Science, 1979, 8(2):189-201. doi: 10.1016/0304-3975(79)90044-6 CrossRef Google Scholar
[2]	LOVÁSZ L, PLUMMER M.Matching Theory[M].New York:North-Holland Press, 1986. Google Scholar
[3]	ZHANG H P.The Connectivity of Z-Transformation Graphs of Perfect Matchings of Polyominoes[J].Discrete Mathematics, 1996, 158(1-3):257-272. doi: 10.1016/0012-365X(95)00048-2 CrossRef Google Scholar
[4]	YAN W G, ZHANG F J.Enumeration of Perfect Matchings of a Type of Cartesian Products of Graphs[J].Discrete Applied Mathematics, 2006, 154(1):145-157. doi: 10.1016/j.dam.2005.07.001 CrossRef Google Scholar
[5]	LI S L, YAN W G.The Matching Energy of Graphs with Given Parameters[J].Discrete Applied Mathematics, 2014, 162:415-420. doi: 10.1016/j.dam.2013.09.014 CrossRef Google Scholar
[6]	DONG F M, YAN W G, ZHANG F J.On the Number of Perfect Matchings of Line Graphs[J].Discrete Applied Mathematics, 2013, 161(6):794-801. doi: 10.1016/j.dam.2012.10.032 CrossRef Google Scholar
[7]	CHANG A, SHIU WC.On the k^th Eigenvalues of Trees with Perfect Matchings[J].Discrete Mathematics and Theoretical Computer Science, 2007, 9(1):321-332 Google Scholar
[8]	唐保祥, 任韩. 2类偶图完美匹配的数目[J].西南大学学报(自然科学版), 2012, 34(10):91-95. Google Scholar
[9]	唐保祥, 任韩.3类特殊图完美对集数的计算[J].南开大学学报(自然科学版), 2014, 47(5):11-16. Google Scholar
[10]	唐保祥, 任韩.4类图完美匹配的计数[J].武汉大学学报(理学版), 2012, 58(5):441-446. Google Scholar
[11]	唐保祥, 任韩.几类特殊图完美匹配数目的递推求法[J].西南师范大学学报(自然科学版), 2014, 39(2):9-13. Google Scholar
[12]	唐保祥, 任韩.两类图完美匹配的计数公式[J].吉林大学学报(理学版), 2016, 54(4):790-792. Google Scholar
[13]	唐保祥, 任韩.2类图完美匹配数目的解析式[J].中山大学学报(自然科学版), 2016, 55(4):15-17. Google Scholar
[14]	唐保祥, 任韩.2类特殊图中的完美匹配数[J].浙江大学学报(理学版), 2017, 44(3):266-269. Google Scholar
[15]	黄丽娜, 李沐春, 刘海忠.图的邻点可区别V-全色数的一个上界[J].西南大学学报(自然科学版), 2017, 39(12):81-85. Google Scholar
[16]	王文霞.无向无权图同构判别算法[J].西南师范大学学报(自然科学版), 2017, 42(3):141-145. Google Scholar

Message Board

Two Types of Nested Recursive Methods for Finding Counting Formulas of Perfect Matching Number

Abstract

References

Access History

通讯作者: 陈斌, bchen63@163.com

Article Metrics

Access History

Other Articles By Authors