-
最优化理论作为一门应用性强的学科,是运筹学的重要构成部分[1],而求解最优化方法的常用方法之一是共轭梯度法[2],其在算法收敛速度、存储需求等方面的综合性能要优于最速下降法和牛顿法,因此共轭梯度法用来求解无约束优化问题[3],特别是大规模的优化问题,在化学、经济和工程设计等领域具有较多应用,成为应用领域人员的热点研究对象.
对于连续可微函数f(x),其无约束优化问题表示为
$\min\limits _{x \in R} f(x)$ ,对于求解上述优化的函数共轭梯度法可用如下描述来表示:k为迭代次数,确定当前迭代点xk的搜索方向dk,该方向即为目标函数f(xk)的下降方向,由搜索步长αk得到下一个迭代点xk+1=xk+αkdk. gk=▽(xk)为梯度,则搜索方向与梯度的关系为当式(1)中搜索方向确定,选择一个合适的搜索步长尤为关键,常见的线搜索方法有:标准Armijo法、Goldstein步长规则、Wolf步长规则和强Wolf步长规则等.
1.标准Armijo法,设β>0,γ∈(0,1),取步长αk=βγmk,其中mk是满足下式的最小非负整数
式(2)中σ∈(0,1).
2. Goldstein步长规则[4]
式(3)中
$\sigma \in\left(0, \frac{1}{2}\right)$ ,当α>0足够小的时候,第2个式子一定不成立.3. Wolf步长规则
式(4)中0 < σ1 < σ2 < 1,αk>0.
4.强Wolf步长规则
式(5)中
$0 < \sigma_{1} < \sigma_{2} < \frac{1}{2}$ ,αk>0.共轭梯度算法中βk为一个关键参数,常见的βk选择方式主要有HS(Hestenes-Stiefel),PRP,DY和CD(Conjuate-Descent)等方法,不同的共轭梯度法具有不同的βk表达式,PRP方法和DY(Dai-Yuan)方法[5-6]的表达式分别为
PRP方法在迭代速度方面具有优势,劣势就是全局收敛性差;DY方法则相反,其最大的优点即全局收敛性好,缺点为对搜索步长的要求较高.周雪琴[7]给出了具有充分下降性的新共轭梯度法及全局收敛性,给出了一种新的βk表达式,并证明了在强Wolfe搜索条件下的全局收敛性.何晓旭等[8]将FR(Fletcher-Reeves)方法与PRP方法混合,新方法具有算法效率高,所需存储量小,不需要外来参数等优点,其公式为
车彩丽[9]中给出了混合HS-DY共轭梯度算法,该算法的优点是具有更好的收敛性,且数值表现更优越、误差更小.刘玲等[10]提出了一种带参数的混合共轭梯度算法,该算法的优点是不依赖线搜索的前提下,使得搜索方向满足充分下降条件,其缺点是在搜索过程中需要引入重新开始的策略,降低计算效率.常见的谱共轭梯度法公式为
本文对以上方法进行综合分析,并在此基础上提出了一种新混合共轭梯度法公式,该方法采用强Wolf步长搜索法则,解决了计算量大的问题,提高了计算效率,且具有全局收敛性和较好的数值特性.
HTML
-
结合PRP方法、DY方法、BFGS方法的优点,本文提出一种改进的混合共轭梯度法
式(9)中Qk+1是一个N×N的矩阵,表达式为
式(10)中sk=dk-dk-1,zk=gk-gk-1. θk+1是典型方法中常用的搜索方向,由BFGS算法及搜索思想,可以得到式(10)中本文提出的新混合共轭梯度法公式.对于Hessen矩阵,该算法用近似方法直接取代直接求解方法,在强Wolfe线搜索条件下,可以得到本文算法具有如下性质
图 1是改进的混合共轭梯度法算法流程图,其中k为迭代步数,从式(9)、式(10)中可以得到βk,式(5)中是强Wolf步长规则.
对于本文算法,如果满足|f(xk+1)-f(xk)|≤eps,则算法终止迭代,其中,eps是较小的正数,eps的选取一般由经验人为给定.
-
对于全局收敛性,如果满足如下条件,则说明算法具有全局收敛性.满足条件:对于任意初始点,算法开始并产生的迭代能够收敛到最优.本文采用反证法来进行收敛性证明,具体描述如式(12).
如果满足上式,则认为算法为弱收敛,即满足条件:只有目标函数导数下界的极限需要接近零.在这里引入2个引理:
引理1 对该混合共轭梯度算法,步长选择法采用强Wolfe规则,则有如下表达式成立
证 由于φk(α)=f(xk+αdk)在α>0时存在下界,故射线φ(α)=f(xk)+σ1αgkTdk与φk(α)在正半轴上有交点,令该最小交点为α′,则有以下表达式成立
利用中值定理可得,存在α″∈(0,α′)使得式(15)成立
根据强Wolfe步长搜索条件,由式(14)和式(15)可得
由此可得gkTdk < 0,引理1得证.
引理2 对于任意的k,有以下不等式成立
由数据归纳法可知,当k=0时d0=-g0,上式显然成立;先需要验证在k>0时该不等式也成立,则通过FR计算公式有
由引理1可得
利用归纳假设对上式中不等式右侧的项进行处理可得
由此,引理2得证.从引理2我们可得如下不等式
在全局收敛性的证明中还需要满足2个条件.
1.目标函数有界
2.函数f(x)连续可微,其导函数g(x)是Lipschitz连续的
首先由式(5)中强Wolf线性搜索步长规则可以得出
结合引理1与βk-1的公式,可得dk的递推表达式
将式(25)中的‖dk-1‖2进行代换,由此可得反复的迭代不等式
根据式(12),当满足式(12)中条件则认为该算法收敛,使用反证法来证明本文算法具有收敛性,首先假设不收敛,则存在一常数ε>0,使得式(27)成立
根据假设1可知gk在水平集上有界,则对于r,ε满足式(28)中表达式
将式(28)对式(26)进行不等式放缩,得到式(29)成立
其中η为一常数.同时由引理2可知
由
$\sigma_{2} < \frac{1}{2}$ 和式(31)可知常数τ>0,使得如下表达式成立由于级数
$\sum\limits_{k=0}^{\infty} \frac{1}{k+1}$ 是发散的,可以得到$\sum\limits_{k=0}^{\infty} \cos ^{2} \theta_{k}$ 也是发散的.另外,梯度函数g(x)满足Lipschitz连续条件,则有从式(32)中可以得出
由强Wolf步长选择法则可得
对于以上证明过程可知,当数列f(xk)是单调下降且有下界的,则‖gk‖2cos2θk是收敛的.另外,由‖gk‖≥ε,可得
$\sum\limits_{k=0}^{\infty} \cos ^{2} \theta_{k}$ 是收敛的.这样的证明结果与结论相互矛盾,从而得到假设‖gk‖≥ε是不成立的,本文算法的收敛性得证.
-
上节中证明了本文的混合共轭梯度法的全局收敛性,本节中结合共轭梯度法一些经典和改进的算法与我们提出的新改进混合共轭梯度法进行对比.参数设置为δ=0.01,σ=0.1,算法的终止条件为‖gk‖≤1×10-6,或迭代次数大于9 000. 表 1是实验中采用的测试问题范例,以表 1中问题进行比对实验.
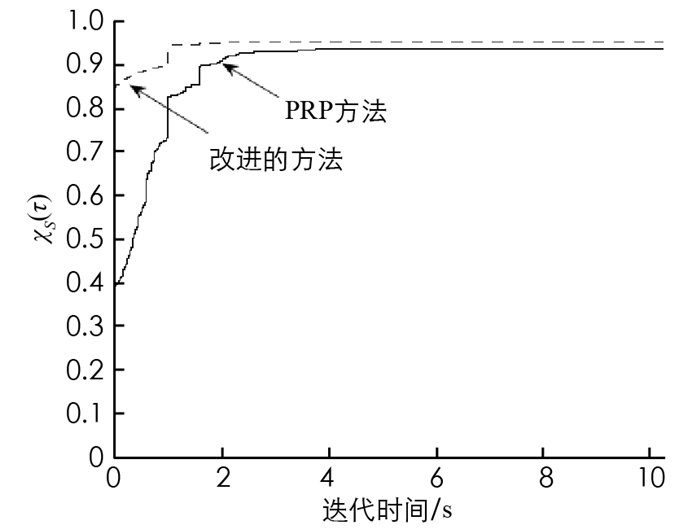
图 2所示是本文方法与PRP共轭梯度算法在迭代时间方面的性能比较,从图 2中分析可知,本文方法的迭代时间要少于传统的PRP共轭梯度法.
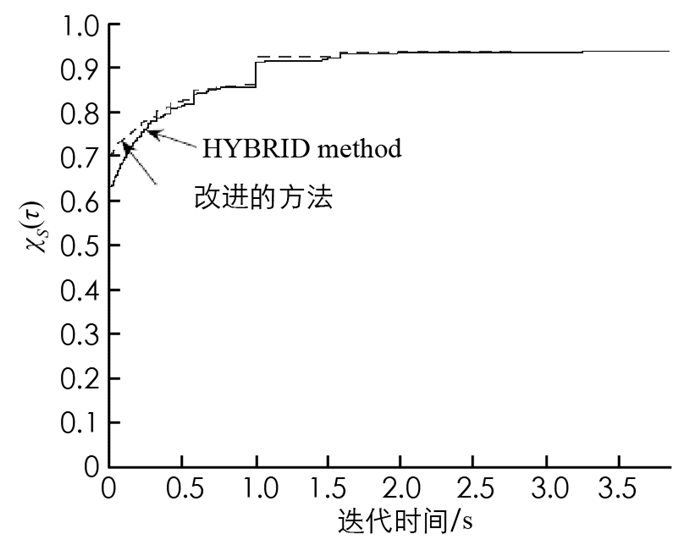
图 3是本文方法和HYBRID方法在迭代时间性能上的对比,从实验结果分析可知,本文方法在迭代时间上要优于HYBRID方法.在实际实验中,本文方法的运行时间比普通共轭梯度法减少了10%左右.因此,通过以上实验结果分析可知,本文提出的改进混合共轭梯度法要优于经典共轭梯度法.
-
本文在已有共轭梯度算法求解无约束优化问题的基础上,提出了一种新混合共轭梯度方法,并给出了在强wolfe线搜索条件下的全局收敛性证明.实验结果表明,本文方法在迭代时间性能方面要优于PRP方法和HYBRID方法.







 DownLoad:
DownLoad: