-
鉴于现代物流运输体系的发展趋势,国内外学者对多式联运的研究日趋增多.在微观技术层面,由于多式联运网络规模大、体系复杂,现有研究大致可以分为两类:第一类是把路径优化问题当作一个决策优化问题,考虑各种约束条件下的目标函数,通过联运网络分析或改造,建立各种模型和设计各种求解算法;另一类是把路径优化问题看成一个评价决策问题,通过构建各种评价指标,应用决策理论和评价方法进行处理.在微观技术层面,国外学者采用最短路径算法[1-3]、松弛分解技术[4]、Martins算法[5]或元启发式算法[6]等进行路径优化.国内学者对多式联运路径优化选择方面的研究成果也非常丰富,如通过构造虚拟运输网络再利用Dijkstra算法或动态规划方法进行优化求解[7-8],或将时间偏离或时间延误处理成惩罚成本加入运输成本中再构建智能算法优化[9-10].构造虚拟网络的方法通常仅适用于问题规模较小和考虑因素极少的情形,将时间因素转换成惩罚函数或惩罚因子的单目标建模方式不完全适合实际情况,因为现实中还需要考虑物流企业的信誉度、口碑或市场份额等.为此,有学者通过构建多目标多式联运数学模型,利用简单给定的权重或某种方法计算的权重等加权多个目标[11-13],但这些研究中给定的权重过于主观简单,不能很好地反映多目标优化问题的实质.
为此,有学者将多式联运的多种重要因素看作属性,引入多属性决策方法[14-18]对备选方案进行评价,这些研究从多属性的角度将所有可供选择的路径或运输方式全部找出然后评价,仅适合问题规模较小的情况,因为当问题规模较大和联运网络比较复杂时,找出所有的备选方案非常困难.文献[19-28]针对这一问题进行了优化和改进.
目前针对多目标优化的方法有很多,各种算法都有其各自的优缺点.本文基于已有研究,从多式联运路径优化角度入手,将运输总成本和运输过程中作业不准点到达城市节点的延误总时间看作两个不同的目标,为了在算法中比较各备选方案的适应度,引入基于多个目标值的优势排序数概念,给出了若干个优势排序数的性质,说明了优势排序数适合作为智能算法的适应度函数,并利用Pareto支配关系判断非劣解,提出一种基于优势排序数计算适应度的符号编码多目标粒子群算法,结果表明该方法具有很好的效果.
HTML
-
多式联运是指托运人只需向货物承运方按一种费率缴纳费用,由多式联运经营人以两种或两种以上的运输方式将货物从接运地运至目的地交付收货人的联合物流形式.多式联运可以避免多次办理单一运输方式时手续多、易出错等缺点,为货物托运人提供一站式服务.由于运输过程中存在多种运输方式,为了实现货物运输过程中运输总成本尽可能小、运输时间尽可能短等目标,货物的运输配送需要从一种运输方式转到另一种运输方式,如何合理选择运输路线和转换节点,是一个具有重大价值和意义的研究课题.
考虑多式联运问题如下:某次作业依次从发货点顺序经过一系列城市节点,最后到达收货点,任意相邻城市之间都存在多种运输方式,暂不考虑运输方式的运量限制,但不同运输方式的转换有转换时间和转换服务成本,在部分城市还有服务时间,不在服务时间窗到达的情形可能需要支付昂贵的额外费用.
按照数学建模的思想,考虑如下模型假设:
假设1 仅考虑单一作业运输,不考虑多个作业混合运输,且假设作业量不超过任一种运输方式的限制;如果某一条路径上的运输方式的可承载量小于该作业的运量,则在联运网络中预先将该运输方式删除.
假设2 通常的货物运输都是一次性整批装载运输,且几乎不会在路径上换装,为此假设作业仅在城市节点处整批装载运输,不在子路径上装载.
假设3 由于作业不能分开运输,故假设货物运输时任意两个城市间只能选择一种运输方式.
假设4 如果在某个城市需要转换运输方式,则只允许转换一次.
假设5 不考虑货物在发货点和收货点装卸货物的库存或看管等费用,或者认为这笔费用已经隐含在联运网络中了.
假设6 如果货物在中间城市按时到达,即在服务时间窗内到达,无需支付额外费用;如果超出该服务时间窗,则需支付额外的费用.对于没有服务时间窗要求的城市,假设其服务时间窗为[0,+∞).
变量及符号说明:xi,jk=1表示在城市i到i+1的路径上选择了运输方式k,取0表示不选择运输方式;ωikl=1表示在城市i处从运输方式k转换到运输方式l,取0表示不发生转换;A表示联运网络上的城市集合,M表示模型所考虑的运输方式集合;Ci,i+1k和Ti,i+1k分别表示从城市i到i+1上的运输方式k的单位运输成本和运输时间;ATi表示作业到达城市i的时间点,[ETi,LTi]表示城市i处的服务时间窗;SCikl和STikl分别表示在城市i处由运输方式k转换到l时的单位中转成本和中转时间.
根据上述假设和数学符号,如果作业不在服务时间窗到达,需要支付昂贵的额外费用,但这笔费用很难估算,为此将整个多式联运作业过程中发生的不准点延误时间作为一个目标考虑,再考虑运输过程中发生的运输总费用,包括运输成本和中转成本,计算公式分别参见式(1)和式(2):
建立下述约束条件表达式
其中:约束式(3)表示在每个城市处能且只能选择某一种运输方式;约束式(4)表示运输方式转换只能发生在城市处,且每个城市处最多只能中转一次;约束式(5)-(7)确保作业运输任务不中断执行;约束式(8)用来计算作业到达城市i+1的时间;约束式(9)表示作业不在服务时间窗到达城市i的不准点延误时间;约束式(10)表示决策变量和中转变量的取值范围.
从上述目标式(2)和约束式(9)可以发现,该模型可看作普通无时间窗多式联运问题的推广,这是因为,当所有城市节点都没有服务时间窗限制,按照假设6将其服务时间窗设置为[0,+∞]后,物流作业在任一城市处的不准点延误时间均为0,总的不准点延误时间为0,从而多目标问题变化为仅仅针对单一目标(此时为运输总费用)的问题.另外,若能通过考察获得所有城市节点处货物不准点到达所需的额外费用,也很容易将第二个目标转化为运输成本.
-
粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的演化计算方法[29],其优势在于简单易于实现并无需太多的参数调整,目前已成功应用于路径规划领域[30-31],但鲜有学者将其应用于多式联运中运输方案的选择.下面给出本文多目标粒子群算法(Multi-objective Particle Swarm Optimization,MPSO)的基本思想及技术要点.
-
为利用粒子群算法求解,首先需要对问题的解进行编码.考虑到路径上运输方式的运量限制或不存在某运输方式,统一将路径上这类运输方式的单位运输成本设置为无穷大或一个很大的正数.由于问题已经简化为物流作业顺序经过一系列城市,故而城市的数量确定,因为只需考虑相邻两城市间的运输方式.现假设整个物流作业只有m种运输方式可供选择,依次给予编号1到m,这样就得到了运输路线和运输方式融合的字符编码方案.进一步考虑,如果联运网络中作业不是顺序经过一系列城市,则可采用双重编码,建立两个字符串,一个字符串的值表示城市编号,一个字符串的值表示城市之间路径上所选择的运输方式.考虑到联运网络上很多城市之间可能没有直接路径相连,所构造的字符编码易产生无效的编码串,导致算法执行困难,为此引入虚拟运输方式,编码为0,表示该运输方式实际不存在,其运输成本为无穷大.
例如,若物流作业从起点O到目的地D之间顺序经过3个城市A,B,C,用长度为4的一组数字表示某运输方案,如编码(3,1,2,2),表示从O到A选择运输方式3,从A到B选择运输方式1,从B到C选择运输方式2,从C到D选择运输方式2,此时运输路径中城市A,B处均发生了运输方式转换.
-
粒子群算法中每个粒子需要计算其适应度值.为设计适应度函数,本文提出下述总优势排序数概念,并从理论上说明其作为适应度函数的可行性.
设多目标问题描述如下
其中zi(x)为决策变量x的第i个分目标(i=1,2,…,p),Ω为问题可行解集合.
定义 设Ω1⊆Ω,对于给定的决策变量x0∈Ω1,x0在Ω1中基于第i个分目标的优势排序数(Dominance Ranking Number)定义为
x0在Ω1中总优势排序数定义为
从上述定义不难看出,决策变量基于分目标的优势排序数及总优势排序数都是就问题可行解集合的某一个子集合而言的,基于分目标的优势排序数的实质是就单个目标进行排序后比自己差的变量的数目,而总优势排序数是所有分目标的优势排序数之和.直观来看,若某变量在问题可行解集合Ω的某子集合中的总优势排序数越大,则该变量是问题的Pareto解的可能性也越大.对于有限集合Ω,有下述性质:
性质1 设多目标问题的可行解集合Ω是有限集合,则
其中|Ω|表示Ω中的元素个数.
证 这只要注意到每个x∈Ω仅需与Ω中其余|Ω|-1个元素作比较即可.
性质2 设多目标问题的可行解集合Ω是有限集合,则满足
$\max\limits_{ 1≤i≤p}$ DRNi(x)=|Ω|-1的变量x∈Ω是该多目标问题在Ω中的Pareto最优解.证 若x∈Ω满足
$\max\limits_{ 1≤i≤p}$ DRNi(x)=|Ω|-1,则存在i0(1≤i0≤p),使得DRNi0(x)=|Ω|-1.若变量x不是多目标问题在Ω中的Pareto最优解,则一定存在x1∈Ω优于x(x1≠x),从而存在i1∈S={1,2,…,p},使得不论i1是否等于i0均会导致DRNi0(x)≤|Ω|-2,矛盾,因而命题成立.
性质1给出了优势排序数的上界,性质2表明,只要某变量x有一个分目标在有限可行解集合Ω中的优势排序数达到|Ω|-1,则该变量x一定是Pareto最优解,这给出了判断有限可行解集合中Pareto最优解的一个充分条件.
推论1 设多目标问题的可行解集合Ω是有限集合,若在Ω中存在x1,x2,…,xt满足xi≠xj,z(xi)=z(xj),∀i≠j;i,j∈{1,2,…,t},t < |Ω|,且
$\max\limits_{ 1≤k≤p}$ DRNk(xi)=|Ω|-t,∀i∈{1,2,…,t},则x1,x2,…,xt均是该多目标问题在Ω中的Pareto最优解.性质3 设多目标问题在有限可行解集合Ω中存在最佳决策变量,若变量x是Ω中所有分目标优势排序数都是最大的一个,则变量x一定是该问题的最佳决策变量.
证 若存在另一变量x1∈Ω优于x(x1≠x),则存在i∈S={1,2,…,p},使得
则
而这与命题的前提假设矛盾,又由多目标问题在有限集合Ω中存在最佳决策变量,因而该变量即为最佳决策变量.
性质4 设多目标问题在有限可行解集合Ω中存在唯一的最佳决策变量,某变量x是问题可行解集合Ω中总优势排序数最大的一个,则变量x一定是该问题的最佳决策变量.
证 若存在另一变量x1∈Ω优于x(x1≠x),则存在i∈S={1,2,…,p},使得
则
从而有
而这与命题的前提假设矛盾,从而命题成立.
性质5 设多目标问题的可行解集合Ω是有限集合,若变量x*∈Ω满足DRN(x*)=p(|Ω|-1),则x*是多目标问题在Ω中的唯一最优解.
证 由DRN(x*)=p(|Ω|-1)及性质1,可得DRNi(x*)=|Ω|-1,i=1,2,…,p,即∀x∈Ω,x≠x*,均有zi(x*) < zi(x),i=1,2,…,p,从而z(x*) < z(x),因此x*是多目标问题在Ω中的唯一最优解.
性质3和性质4给出了已知多目标问题在有限可行解集合中存在(唯一)最佳决策变量的前提下,寻找最佳决策变量的两个充分条件.性质5不需要预先假设多目标问题存在最优解,可看成是性质4的推广,这是因为证明多目标问题存在最优解或唯一最优解不比找出最优解容易多少.
分析性质2-5,如果在给定的问题可行解集合Ω中能找到符合条件的变量x,则该多目标问题就能很好解决.然而,许多多目标问题的可行解集合Ω比较复杂且很难完全描述出来,更别说找出完全符合上述性质的决策变量了.为此,基于粒子群算法考虑,在每一次迭代产生的粒子群体中寻找总优势排序数较大的粒子个体,则由上述性质1-5可知这些粒子所代表的运输方案也应该较优,从而可以定义粒子个体(决策变量)x的适应度函数为fit(x)=DRN(x).
-
设vkt,xkt分别表示粒子群体中第k个粒子在第t次迭代时的速度和位置,pbestk表示第k个粒子迄今所找到的最优解的位置,gbest表示粒子群体迄今为止适应度最高的粒子位置,w表示惯性权重,c1,c2为粒子的学习因子,本文多目标粒子群算法采用如下公式来更新每个粒子的速度和位置:
其中:round表示取整函数,mod表示求模运算,m表示可供选择的运输方式总数目.另外,若式(15)的值为0,则运输方式实际对应编号为m的运输方式.如果增加了虚拟运输方式,则只需检查该位置对应的两个城市是否存在直接路径即可区分是虚拟运输方式还是编号为m的运输方式.
-
步骤1 输入问题的数据(单位运输成本、运输时间、单位中转成本、中转时间等)及算法的参数(群体粒子数目、最大迭代数、惯性权重w及学习因子c1,c2).
步骤2 随机初始化群体中所有粒子的位置和速度,计算每个粒子个体所具有的运输总成本和运输总时间,根据总优势排序数计算每个粒子的适应度值,初始化每个粒子的历史最优信息pbestk.
步骤3 在当前群体中寻找Pareto最优粒子个体,将其汇总成Pareto最优集;找出当前群体中具有最大适应度的粒子作为当前群体最优粒子,初始化群体历史最优信息.
步骤4 根据式(13)-(15)更新所有粒子的位置和速度,计算所有新粒子个体的运输总成本和运输总时间.
步骤5 在新粒子群体中寻找Pareto最优粒子个体,更新Pareto最优集.
步骤6 计算每个新粒子的适应度,对每个粒子xk,若其适应度优于pbestk,设置当前粒子xk为pbestk.
步骤7 找出新粒子群体中具有最大适应度的粒子,若其优于历史最优粒子,则更新群体历史最优粒子.
步骤8 若不满足停止条件,转步骤4;否则输出算法所获得Pareto最优解集的信息.
2.1. 问题的编码
2.2. 适应度函数的设计
2.3. 粒子的更新
2.4. 算法步骤
-
为了说明本文模型可以直接应用到无服务时间窗的多式联运模型,选择文献[11, 19, 24]的例子验证.取群体粒子数目为20、最大迭代数为20、惯性权重w=1及学习因子c1=0.5,c2=0.8,应用基于优势排序数的多目标粒子群算法获得的Pareto最优解为:运输方式为“公路-航空-铁路-航空”,运输成本为205,不准点延误时间为0.该Pareto最优解也是问题的最优解,该结果也从实例上证实了总优势排序数的性质3-5关于唯一最优解的结论.
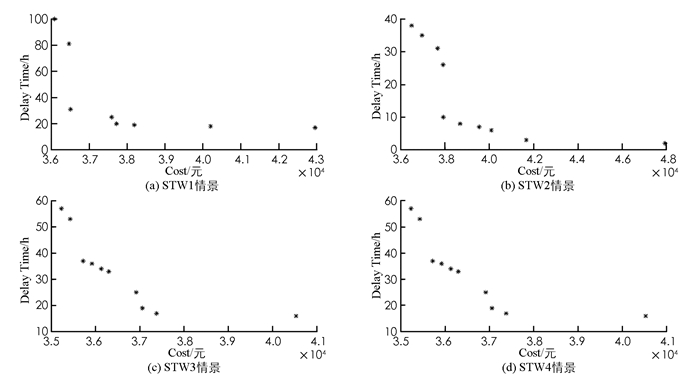
进一步,为分析本文模型和算法的有效性,选择多式联运网络节点数达15个的例子.部分城市节点的服务时间窗数据参见表 1. 表 1中共设置了4个时间窗,其它数据参见文献[7, 10].取群体粒子数目为100、最大迭代数为100、惯性权重w=1及学习因子c1=0.5,c2=0.8. 图 1中给出本文算法针对4种不同的服务时间窗获得的Pareto最优解,且每次运行时间仅为40 s左右,说明该算法速度和效率都令人满意.
-
本文研究了节点带时间窗约束的多式联运问题,将问题建模为多个目标,提出了基于分目标的优势排序数和总优势排序数概念,理论上说明其作为适应度函数的可行性,设计了一种基于优势排序数的多目标粒子群算法进行求解,结果表明该方法不仅能有效处理大规模的多式联运问题,还能较快地获得所有的Pareto最优解.另外,本文的多目标模型可看作无服务时间窗约束多式联运模型的推广,只需要将所有节点的服务时间窗设置为[0,+∞)即可.
本模型将服务时间窗的不满足程度看作一个目标,在后续的研究工作中可考虑将其细分为作业早到和晚到两种情形,以及引入节点处的不同惩罚成本因子或运输方式的班期限制进行研究.文章虽然仅仅考虑了两个目标的多式联运数学模型,但实质上可将更多目标纳入考核范围,只需应用总优势排序数概念和计算公式就可以计算出每一种选择方案的适应度值,从而利用本文粒子群算法求解.在本文算法中,寻找Pareto最优解集合可以适当优化,以节省算法的时间开销,如先根据分目标优势排序数判断是否Pareto最优解,再考虑适应度值较大的若干解.另外,本文还存在许多可进一步研究的空间,如将单一物流作业推广为多个物流作业、多个物流作业整合运输、多个收发点的物流运输、多个物流公司联合运输、货损成本因素、碳排放因素、网络不确定因素等,这些将在以后的研究中进一步完善.






 DownLoad:
DownLoad: