-
非线性偏微分方程在数学、物理、化学以及其它学科和工程领域起着非常重要的作用.很多学者研究了非线性偏微分方程,因此许多求解非线性偏微分方程的方法也发展起来.比如Jacobi椭圆函数展开法[1]、辅助函数法[2]、指数函数法[3]、sine-cosine法[4]、G′/G展开法[5-6]、Bäcklund变换法[7]等.扩展试验方程法是一种常用于求解非线性偏微分方程精确解的方法,文献[8]利用扩展试验方程法得到了广义Benjamin方程和Burger-Kdv方程的精确行波解,文献[9]通过扩展试验方程法考虑了非线性耦合Schrodinger Boussinesq偏微分方程的精确行波解.
本文主要探讨积分微分KP层次方程
的精确行波解,其中
KP层次方程在数学物理和工程中有许多重要的应用,是一类非常重要的非线性偏微分方程.文献[10]利用重复齐次平衡法得到了(3+1)维KP方程的孤子解和周期解,文献[11]通过G′/G-展开法得到了(2+1)维KP方程的行波解.文献[12]通过扩展tanh法得到了耦合KP方程的行波解.我们将对方程(1)进行积分变换,之后再对其进行行波变换,然后利用扩展试验方程法对方程(1)的精确行波解进行研究.
HTML
-
在方程(1)中做变换u=vxx,可将积分微分KP层次方程(1)转换成如下的方程
对方程(2)进行行波变换,再对其进行一次积分,令v(x,y,t)=v(ξ),其中ξ=x+y-kt,k是波速,方程(2)可化为
其中
$v_{\xi\xi}=\frac{\partial^{2} v}{\partial \xi^{2}}, v^{(4)}=\frac{\partial^{4} v}{\partial \xi^{4}}$ ,C是积分常数.令w=vξξ,方程(3)可化为如下等价的方程综上推导可知,方程(4)的解为w=vξξ,而方程(1)的解为u=vxx,显然方程(1)的解与方程(4)的解具有相同形式.为此下面只需对方程(4)进行研究.
-
上节给出了方程(1)的积分变换和行波变换,本节将利用扩展试验方程法对方程(1)的精确行波解进行研究.首先给出扩展试验方程法的步骤.
-
考虑如下的常微分方程
步骤1 假设方程(5)有如下形式的解
其中τi(i=0,1,…,δ)为待定系数,Y满足如下方程
τi,λi,ζi是待常数,可以得到
Φ(Y),Ψ(Y)是关于Y的多项式.
步骤2 平衡最高阶导数项和最高阶非线性项,可得到δ,ζ,λ的关系.
步骤3 把方程(6),(7)代入方程(5)得到关于Y的多项式,令Yi的各项系数为0,得到方程组,解方程组得到τi,λi,ζi.
步骤4 将方程(7)转化为积分形式
根据(9)式可以得到方程(5)的行波解.
-
根据方程(1)与方程(4)解之间的关系,先用扩展试验方程法对方程(4)的精确行波解进行研究.现在应用扩展试验方程法求解方程(4),通过(6),(7),(8)式可以得到
利用齐次平衡法,可以得到δ-2+θ-ε=2δ,即δ=θ-ε-2.
假设ε=0,θ=3,则δ=1,于是有
把(15),(16)式代入方程(4),合并同类项,令Ym(m=0,1,2)的系数等于0,得到代数方程组为
解得
根据方程(9)可知
其中λ3ζ0>0,为了对(19)式进行积分,下面将讨论以下几种情况:
情况1 若
α是非零常数,等式两边系数相等,得到
把(21)式代入(18)式,得到
λ3,ζ0,α,C为任意常数
得到
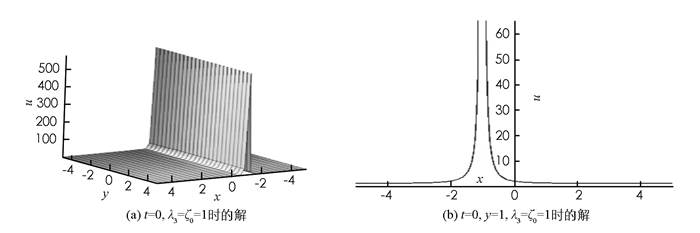
把(22),(24)式代入方程(15),得到方程(1)的钟状解u1(图 1),
其中
情况2 若
其中α1,α2是非零常数,等式两边系数相等,得到
把(27)式代入(18)式,得到
λ3,ζ0,C,α1,α2为任意常数.
当α2>α1时,
得到
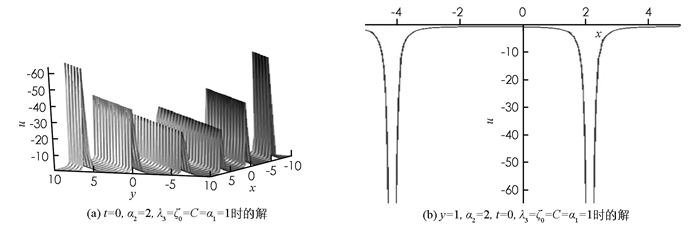
把(28),(30)式代入方程(15),得到方程(1)的三角函数解u2(图 2),
其中
同样地,当α1>α2时,
把(28),(32)式代入方程(15),得到方程(1)的双曲函数解u3,
其中
情况3 若
α1,α2,α3是非零常数,等式两边系数相等,得到
把(35)式代入(18)式,得到
其中λ3,ζ0,C,α1,α2,α3为任意常数,
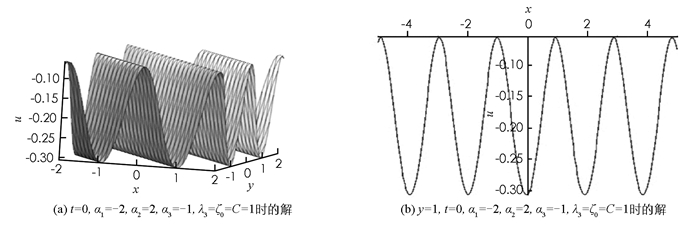
把(36),(37)式代入方程(15),得到方程(1)的椭圆函数解u4(图 3),
其中
2.1. 扩展试验方程法
2.2. 方程(1)的精确行波解
-
利用扩展试验方程法得到了积分微分KP层次方程的钟状解、三角函数解、双曲函数解和椭圆函数解的精确表达式.通过查阅文献,这些解的显示表达式是首次求出的,可以看出扩展试验方程法是求解非线性偏微分方程的有效方法,可以用于求解数学物理中的非线性偏微分方程.






 DownLoad:
DownLoad: