Pure Exact Sequence in the Category of Gorenstein Projective Complexes

除非特别声明，环R是具有单位元的结合环，所有涉及的模均是酉模，Mod R表示左R-模范畴.

定义1^[7]  设$\mathscr{X}$是R-模类，M是左R-模.同态φ：M→C，C∈$\mathscr{X}$，如果对任意的f：M→C′，其中C′∈$\mathscr{X}$，都有同态g：C→C′，使得gφ=f，则称φ是M的$\mathscr{X}$-预包络.若C=C′，f=φ，且满足gφ=φ的g是自同构，则称$\mathscr{X}$-预包络是M的$\mathscr{X}$-包络.

定义2^[7]  如果复形P是投射的，则P是正合的，且对任意的整数n，Z_nP是投射模.

定义3^[8]  如果左R-模M是Gorenstein投射模，则存在一个投射左R-模的正合列

使得M $ \cong $Im(P₀→P_-1)，并且对任意投射左R-模Q，Hom_R(P，Q)是正合的.我们用GProj R记所有Gorenstein投射左R-模构成的范畴.

定义4^[8]  如果复形G是Gorenstein投射的，则存在复形的正合序列X：…→P^-1→P⁰→P¹→P²→…，满足以下条件：

(a) 对∀i∈ $\mathbb{Z}$，Pⁱ是投射复形；

(b) Ker(P⁰→P¹)=G；

(c) 对任意的投射复形P，Hom_C(R)(X，P)是正合的.

我们用GProjC(R)记所有Gorenstein投射复形构成的范畴，用GProjC(R)记所有有限表示Gorenstein投射复形构成的范畴.

定义5^[6]  (a)设0→A→B→C→0是Mod R中的正合列.如果对任意的有限表示模N，序列0→Hom_R(N，A)→Hom_R(N，B)→Hom_R(N，C)→0是正合的，那么称正合序列0→A→B→C→0是纯正合的.

(b) 如果B的子模A为B的纯子模，则$0 \to A \circlearrowleft B \to B/A \to 0$是纯的.

(c) 如果单同态f：A→B是纯单的，则f的象是B的纯子摸.

(d) 如果满同态g：C→D是纯满的，则g的核是C的纯子摸.

通常，R-模复形的正合性被定义为逐点的正合，这种定义方法为理解有界导出范畴提供了方便.

定义6^[9]  如果零调复形X在某个层次n处是纯正合的，则该点处的短正合列0→Ker d_Xn→X_n→Kerd_Xn-1→0是纯正合的.如果对任意的整数n，X在n处纯正合，则复形X是纯零调复形.

定义7^[9]  M如果为Mod R中的纯投射(或内射)模，则M关于每一个纯正合序列是投射的(或内射的).我们将Mod R中的纯投射模和纯内射模构成Mod R的全子范畴分别记为PP，PI.

定义8^[6]  (a)如果GProj R中的正合序列0→G₁→G₂→G₃→0是G-纯正合的，则对任意的有限表示Gorenstein投射模G，序列0→Hom_R(G，G₁)→Hom_R(G，G₂)→Hom_R(G，G₃)→0是正合的.

(b) H如果为GProj R中的纯投射模，则对任意G-纯正合列0→G₁→G₂→G₃→0，序列0→Hom_R(H，G₁)→Hom_R(H，G₂)→Hom_R(H，G₃)→0是正合的.

(c) E如果为GProj R中的纯内射模，则对任意G-纯正合列0→G₁→G₂→G₃→0，序列0→Hom_R(G₃，E)→Hom_R(G₂，E)→Hom_R(G₁，E)→0是正合的.

(d) A如果为GProj R中的绝对纯模，则GProj R中的任意正合列0→A→G₂→G₃→0是G-纯正合的.

我们将GProj R中的纯投射、纯内射和绝对纯模构成的GProj R的全子范畴分别记为PP-GProj R，PI-GProj R和Abs-GProj R.

定义9  (a)如果正合复形F：…→F_n+1→F_n→F_n-1→…是G-纯正合的，则满足以下两条：

(a₁)对∀n∈$\mathbb{Z}$，F_n是Gorenstein投射的；

(a₂)对∀n∈$\mathbb{Z}$，模的短正合列0→Z_nF→F_n→Z_n-1F→0是G-纯正合的.

(b) H如果为GProjC(R)中的纯投射复形，则对复形的任意G-纯正合列0→F¹→F²→F³→0，序列0→Hom_C(R)(H，F¹)→Hom_C(R)(H，F²)→Hom_C(R)(H，F³)0→是正合的.

(c) E如果为GProjC(R)中的纯内射复形，则对复形的任意G-纯正合列0→F¹→F²→F³→0，序列0→Hom_C(R)(F³，E)→Hom_C(R)(F²，E)→Hom_C(R)(F¹，E)→0是正合的.

(d) A如果为GProjC(R)中的绝对纯复形，则GProjC(R)中任意的正合列0→A→F²→F³→0是G-纯正合的.

我们将GProjC(R)中的纯投射、纯内射和绝对纯复形构成的GProjC(R)的全子范畴分别记为PP-GProjC(R)，PI-GProjC(R)和Abs-GProjC(R).

定理1  设A∈GProjC(R)，则下列叙述等价：

(ⅰ) A∈Abs-GProjC(R)；

(ⅱ) 存在GProjC(R)中的G-纯正合序列0→A→P→G¹0，其中P是投射复形；

(ⅲ) 对任意有限表示Gorenstein投射复形N，有Ext_C(R)¹(N，A)=0.

证  (ⅰ)⇒(ⅱ)由GProjC(R)中绝对纯复形的定义可以得证.

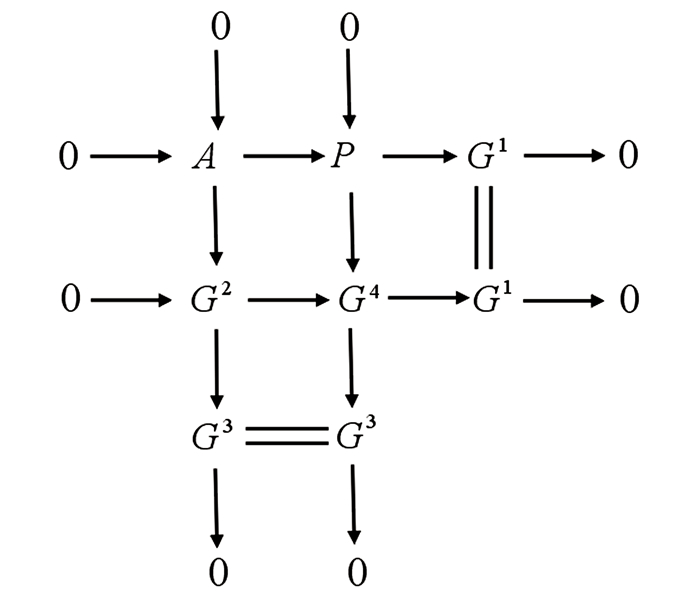
(ⅱ)⇒(ⅰ)  对GProjC(R)中任意的正合序列0→A→G²→G³→0，有如下行列正合交换图(图 1)：

因为Ext_C(R)¹(G³，P)=0，所以图 1第二列可裂.对任意的G∈GProjC(R)，用Hom(G，-)作用于图 1，由蛇引理可知

是正合的.于是0→A→G²→G³→0是G-纯正合的.故A∈Abs-GProjC(R).

(ⅱ)⇔(ⅲ)  对∀G∈GprojC(R)和G-纯正合序列0→A→P→G¹→0，用Hom_C(R)(G，-)作用此正合列得长正合序列0→Hom_C(R)(G，A)→Hom_C(R)(G，P)→Hom_C(R)(G，G¹)→Ext_C(R)¹(G，A)→0.于是(ⅱ)与(ⅲ)的等价易证.

下面我们给出定理1的一些应用.

推论1  Abs-GProjC(R)关于扩张、直和、G-纯子复形封闭.

证  设0→A→B→C→0是GProjC(R)中的G-纯正合列，其中{Aⁱ}_i∈I是范畴Abs-GProjC(R)中的一族绝对纯复形.对∀G∈GProjC(R)，用Hom_C(R)(G，-)作用此正合列，可得正合序列Ext_C(R)¹(G，A)→Ext_C(R)¹(G，B)→Ext_C(R)¹(G，C).因为

所以Ext_C(R)¹(G，B)=0.于是B∈Abs-GProjC(R).故Abs-GProjC(R)关于扩张封闭.

设{Aⁱ}_i∈I∈Abs-GProjC(R).对∀G∈GProjC(R)，由同构

可知${\mathop{\rm Ext}\nolimits} _{c(R)}^1\left( {G, \mathop \oplus \limits_{i \in I} {A^i}} \right) = 0.11111\mathop \oplus \limits_{i \in I} {A^i} \in Abs - {\mathop{\rm GProj}\nolimits} C(R)$, 故Abs-GProjC(R)关于直和封闭.

设0→A→B→C→0是GProjC(R)中的G-纯正合列，其中B∈Abs-GProjC(R).对∀G∈GProjC(R)，用Hom_C(R)(G，-)作用此正合列可得长正合序列0→Hom_C(R)(G，A)→Hom_C(R)(G，B)→Hom_C(R)(G，C)→Ext_C(R)¹(G，A)→Ext_C(R)¹(G，B)→….因为Ext_C(R)¹(G，B)=0，所以Ext_C(R)¹(G，A)=0.于是A∈Abs-GProjC(R).故Abs-GProjC(R)关于G-纯子复形封闭.

定义10  如果Gorenstein投射复形M是FP-投射的，则对任意的N∈Abs-GProjC(R)，有Ext_C(R)¹(M，N)=0. GProjC(R)中的所有FP-投射复形构成的类记为FP-GProjC(R).

命题1  设R是环，M∈GProj C(R).则以下条件等价：

(ⅰ) M∈FP-GProjC(R)；

(ⅱ) M相对于GProjC(R)中的任意正合序列0→A→B→C→0是投射的，其中A∈Abs-GProjC(R)；

(ⅲ) 对GProjC(R)中的任意正合序列0→K→F→M→0，其中F∈Abs-GProjC(R)，K→F是K的Abs-GProjC(R)-预包络；

(ⅳ) M是Abs-GProjC(R)-预包络KP的余核，其中P是投射复形，K是Gorenstein投射复形.

证  (ⅰ)⇒(ⅱ)设0→A→B→C→0是GProjC(R)中的正合序列，其中A∈Abs-GProjC(R).因为M∈FP-GProjC(R)，所以Ext_C(R)¹(M，A)=0.于是0→Hom_C(R)(M，A)→Hom_C(R)(M，B)→Hom_C(R)(M，C)→0是正合的.故(ⅱ)得证.

(ⅱ)⇒(ⅰ)  对∀A∈Abs-GProjC(R)，存在GProjC(R)中的短正合序列0→A→P→L→0，其中P是投射复形.则序列

是正合的.由(ⅱ)知序列

是正合的.则Ext_C(R)¹(M，A)=0.故M∈FP-GProjC(R).

(ⅰ)⇒(ⅲ)  设E∈Abs-GProjC(R).对GProjC(R)中的正合列0→K→F→M→0，其中F∈Abs-GProjC(R)，由(ⅰ)知0→Hom_C(R)(M，E)→Hom_C(R)(F，E)→Hom_C(R)(K，E)→0是正合的.故(ⅲ)成立.

(ⅲ)⇒(ⅳ)  对M存在正合列0→K→P→M→0是GProjC(R)中的正合列，其中P是投射复形，K是Gorenstein投射复形.由定义知P∈Abs-GProjC(R).因此K→P是K的Abs-GProjC(R)-预包络.

(ⅳ)⇒(ⅰ)  由(ⅳ)可知，存在GProjC(R)中的正合序列0→K→P→M→0，其中K→P是K的Abs-GProjC(R)-预包络，P是投射复形.任取N∈Abs-GProjC(R)，则序列0→Hom_C(R)(M，N)→Hom_C(R)(P，N)→Hom_C(R)(K，N)→Ext_C(R)¹(M，N)→0是正合的.再次由(ⅳ)可知

是正合的.因此Ext_C(R)¹(M，N)=0.故M∈FP-GProjC(R).