Iteration Method of Correcting Characteristic Value to Ill-Posed Total Least Squares Based on Signal-to-Noise Ratio

考虑函数模型

其中：L为n×1维观测向量，A为n×t维设计矩阵，rank(A)=r≤t，X为t×1未知参数向量，n×1维向量Δ为随机向量的观测误差.依据最小二乘原理得到法方程为

其中：N = A^TA，W = A^TL. (2)式两边加上$\boldsymbol{\hat X} $，利用迭代求解得^[12]

若记q =(N + E)^－1，则(3)式转化为

(3)，(4)式称为谱修正迭代公式.谱修正迭代法既改善法方程的病态性，又不改变方程的等量关系，而且保留了最小二乘估计无偏的优良性质.

总体最小二乘平差函数模型为

其中Δ_L，Δ_A分别为观测向量随机误差和系数矩阵误差.为了便于讨论问题，设

vec(·)表示矩阵的拉直变换算子.将(5)式表示为误差方程式形式

记E =(E_A e)，限制约束条件$ \|\boldsymbol{E}\|_{F}=\left(\operatorname{tr}\left(\boldsymbol{E}^{\mathrm{T}} \cdot \boldsymbol{E}\right)\right)^{\frac{1}{2}}=\min $等价于

整理得

将(9)式两边加上$\boldsymbol{\hat X} $整理得

其中$\mu=1+\frac{(\boldsymbol{A} \boldsymbol{\hat X} -\boldsymbol{L})^{\mathrm{T}}(\boldsymbol{A} \boldsymbol{\hat X} -\boldsymbol{L})}{1+ \boldsymbol{\hat X} ^{\mathrm{T}} \boldsymbol{\hat X} }$，由此得到病态总体最小二乘的谱修正迭代法计算公式.从(10)式可以看出，病态总体最小二乘的谱修正迭代解在一定程度上减少了法矩阵的条件数，从而法方程的病态性得到相应的改善，但是病态性仍然存在.在此基础上文献[17]借用岭估计的思想对(10)式进行了修正，得到了总体最小二乘谱修正迭代的改进算法.将(9)式两边加上δ$\boldsymbol{\hat X} $整理得

其中：$ \mu=\delta+\frac{(\boldsymbol{A} \boldsymbol{\hat X} -\boldsymbol{L})^{\mathrm{T}}(\boldsymbol{A} \boldsymbol{\hat X} -\boldsymbol{L})}{1+ \boldsymbol{\hat X} ^{\mathrm{T}} \boldsymbol{\hat X} } $，δ为谱修正参数.谱修正迭代的改进算法很大程度上减少了法矩阵的条件数，使得法方程的病态性得到有效改善.

上述两种病态总体最小二乘谱修正迭代算法减少了法矩阵的条件数，改善了法方程的病态性，但是过于粗略，降低了解的精确性.线性模型中的病态性则表现为复共线性，这些算法明显缺乏对复共线性危害的诊断和度量.为了实施更精准的正则化策略，必须理清哪些参数估计受到复共线性危害.文献[18]通过计算如下的信噪比估计量将每个待估参数的估计效果区分开来，

其中：$ {\hat X _k} $为第k个参数的LS估计，$\boldsymbol{\hat e} = \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A}}\boldsymbol{\hat X} $为残差向量.文献[18]给出检验法则为：当F_k≤F_{1，n－r，χ1²(γ)}(α)时，复共线性对相应参数估计${\hat X _i}$的危害比较严重，其估计效果不好；当F_k>F_{1，n－r，χ1²(γ)}(α)时，复共线性对相应参数估计${\hat X _i}$的危害比较小，其估计效果较好(α为显著性水平，F_{1，n－r，χ1²(γ)}(α)是非中心F分布F_{1，n－r，χ1²(γ)}的上侧α分位点).

由此对(9)式两边加上$\sigma \mathit{\boldsymbol{R}}\boldsymbol{\hat X} $整理得

其中：$ \mu = \frac{{{{(\mathit{\boldsymbol{A}}\boldsymbol{\hat X} - \mathit{\boldsymbol{L}})}^{\rm{T}}}(\mathit{\boldsymbol{A}}\boldsymbol{\hat X} - \mathit{\boldsymbol{L}})}}{{1 + {{\boldsymbol{\hat X} }^{\rm{T}}}\boldsymbol{\hat X} }} $，σ为谱修正参数，R为谱修正矩阵.根据信噪比检验，谱修正矩阵$\boldsymbol{R}=\left(\begin{array}{cc} \boldsymbol{\theta}_{t_{1}} & \boldsymbol{o} \\ \boldsymbol{o} & \boldsymbol{I}_{t-t_{1}} \end{array}\right) $位于法矩阵中亟待修正的部位，修正达到什么程度取决于谱修正参数σ. (13)式称为基于信噪比检验的病态总体最小二乘谱修正迭代法，该方法针对设计阵的部分数据列的复共线性关系构建了精准有效的修正策略，从而有节制地减少法矩阵的条件数，最大程度上改善法方程的病态性.

基于信噪比检验的病态总体最小二乘谱修正迭代法的算法步骤如下：

1) 选取适当的参数初始迭代值$\boldsymbol{\hat X} $⁽⁰⁾；

2) 计算$\mathit{\boldsymbol{M}} \buildrel \Delta \over = \frac{{{{\left( {\mathit{\boldsymbol{A}}{{\boldsymbol{\hat X} }^{(i)}} - \mathit{\boldsymbol{L}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{A}}{{\boldsymbol{\hat X} }^{(i)}} - \mathit{\boldsymbol{L}}} \right)}}{{1 + {{\boldsymbol{\hat X} }^{(i)}}{\;^{\rm{T}}}{{\boldsymbol{\hat X} }^{(i)}}}}{\boldsymbol{\hat X} ^{(i)}} + \sigma \mathit{\boldsymbol{R}}{\boldsymbol{\hat X} ^{(i)}}$；

3) 计算$\boldsymbol{\hat X} $⁽ⁱ⁺¹⁾=(A^TA +σR)^－1(A^TL + M)；

4) 重复2)，3)两个过程，当‖$\boldsymbol{\hat X} $⁽ⁱ⁺¹⁾－$\boldsymbol{\hat X} $⁽ⁱ⁾‖ < ε时，迭代停止，ε为给定的较小阈值.

算例1  考虑模拟空间测边网^[19]，P₁，…，P₁₀为10个已知点，而且知道10个已知点到3个未知点P₁₁，P₁₂，P₁₀(假设模拟值分别为(0，0，0)，(68，-26，9)，(14，41，-11))的观测距离及3个未知点之间的观测距离.要求根据33个观测距离确定3个未知点的9个坐标，其中观测量为等精度，中误差为±0.01 m.令设计阵A和观测量L模拟均值都为零，单位权方差分别为0.001，0.01，满足正态分布的偶然误差.若计算中3个坐标近似值分别取为P₁₁(－0.01，0.02，0.00)，P₁₂(68.01，－25.98，8.98)，P₁₃(14.02，41.02，－10.98)，则法矩阵的奇异值为11.264 8，8.830 0，7.997 5，3.932 4，2.677 3，1.243 6，0.045 6，0.003 7，0.000 5，其法矩阵的条件数约为2.4×10⁴，病态性严重.通过计算LS估计的信噪比估值，根据文献[18]中的做法取阈值d=121.34，显著性水平α=0.05，临界值c=F_{1，24，121.34}(0.05)=71.88，结果如表 1所示，其中3个LS估计的分量所对应的信噪比估值(0，26，65)较小，而有6个LS估计的分量所对应的信噪比估值较大，超过临界值.说明有6个参数的估计效果较好，3个参数的估计效果不好.谱修正矩阵$\mathit{\boldsymbol{R}}{\rm{ = }} \left(\begin{array}{ll} \boldsymbol{o}_{6} & \boldsymbol{o} \\ \boldsymbol{o} & \boldsymbol{I}_{3} \end{array}\right)$，L曲线法的谱修正参数σ=1.95.对未知点的坐标估值结果见表 2，其中：方法1为总体最小二乘解法；方法2为总体最小二乘谱修正迭代解法；方法3为总体最小二乘谱修正迭代改进解法；方法4为基于信噪比检验的总体最小二乘谱修正迭代解法.从表 2看出，基于信噪比检验的总体最小二乘谱修正迭代解法的相对误差最小，效果最好.

例2  卫星导航定位、信号图像处理等问题模型为如下第一类Fredholm积分方程^[20]

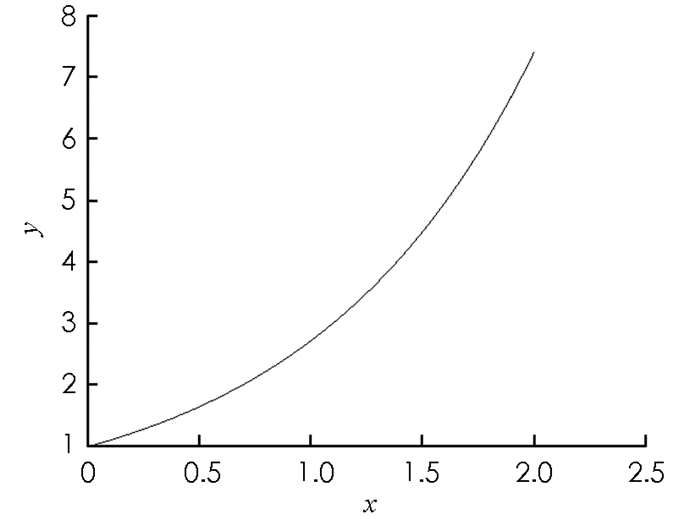
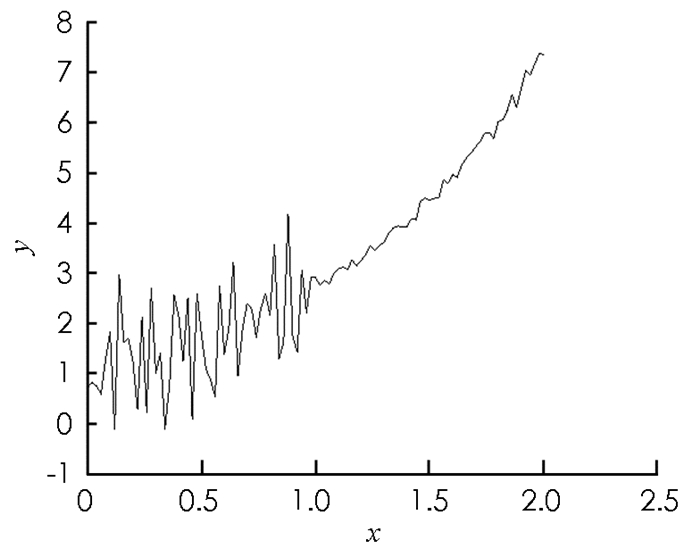
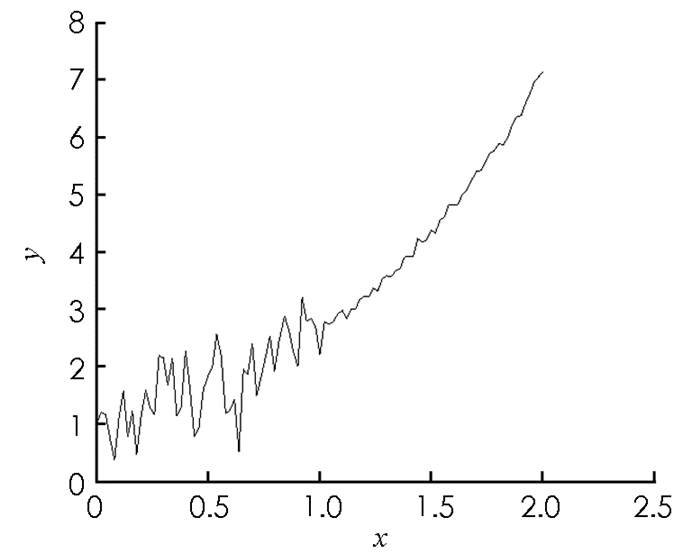
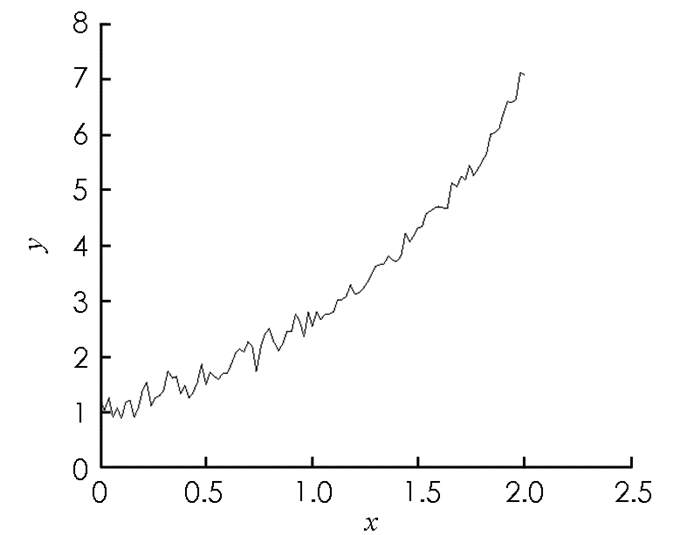
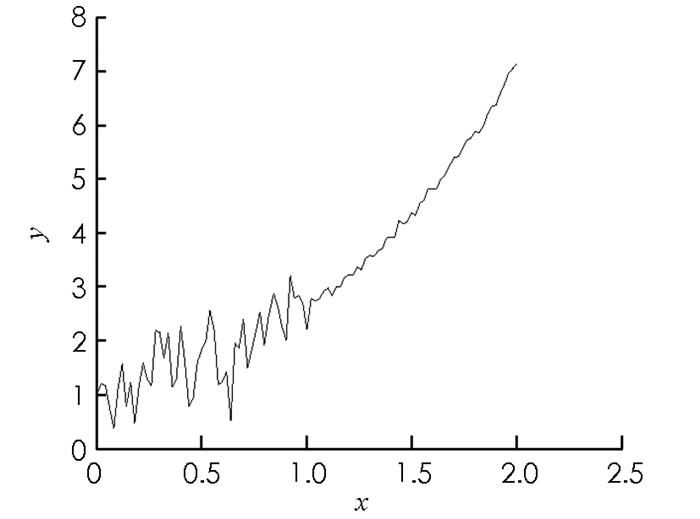
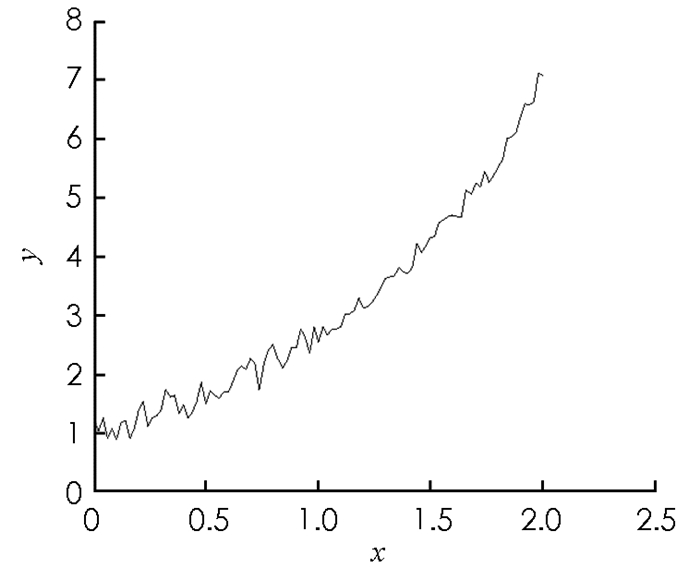
核函数为K(x，y)=e^xy，f(x)的精确解函数为f(x)=e^x，在区间[0，2.5]内的形状如图 1所示.采用数值解法离散核函数算子，得到线性方程组y = Ax，A的元素为a_ij=e^x_iy_j，x，y分别是在x∈[0, 1]区间内采用间隔为0.02的f(x_i)，z(y_j).采样点数i=201，j=101.构造201×51的矩阵A₁，条件数为6.11×10²，A₁为病态矩阵；构造201×50的随机矩阵A₂的元素，条件数为2.34，A₂为非病态矩阵.对设计阵与z(y_j)分别模拟零均值，单位权方差为0.001，满足正态分布的偶然误差，得到总体最小二乘平差模型. 5种解的精度比较见表 3，其中：方法1为最小二乘解法；方法2为总体最小二乘解法；方法3为总体最小二乘谱修正迭代解法；方法4为总体最小二乘谱修正迭代改进解法；方法5为基于信噪比检验的总体最小二乘谱修正迭代解法.利用以上5种解法求解离散化的函数f(x_i)，计算结果如图 2-6所示.

对于病态积分方程，最小二乘和总体最小二乘的计算效果都不理想，通过谱修正迭代之后得到的函数解有所改善，相比较而言基于信噪比检验的总体最小二乘谱修正迭代算法的效果最好，得到的函数图形和真值最接近.另外，由表 3可以看出，基于复共线性诊断的谱修正迭代法仅仅是对受到复共线性危害的参数起作用，而对没受到危害的参数尽量减少修正过程对其产生的负面影响，相应的谱修正方案精准而有效.

分析算例1中的表 1、表 2和算例2中的表 3、图 2-6可以得出如下结论：

1) 法矩阵病态时，最小二乘解和总体最小二乘解严重偏离函数真值，谱修正迭代算法对函数估值有所改善，而基于信噪比检验的总体最小二乘谱修正解效果最优.

2) 法矩阵严重病态时，最小二乘解和总体最小二乘解很不稳定，一般谱修正迭代算法也没有很好提高数值稳定性，而是更具针对性的修正策略方法达到误差最小.

3) 法矩阵严重病态时，基于复共线性诊断的谱修正迭代法所得估值的相对误差最小，说明估计效果较好，有效地减少了法矩阵的条件数，很好消除了法矩阵病态性的危害，提高了参数估值的有效性和稳定性.

4) 在实施谱修正迭代的过程中要避开没有受到复共线性危害的参数，正常求解算法已经很好，不需要干扰这些参数求解过程.