Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2020 Volume 45 Issue 3
Article Contents
Previous Article Next Article

Chuan-ju QU, Jiao-ping YANG. On Arbitrage Strategy of Stock Index Futures Based on Wavelet De-Noising and Co-Integration Theory for High Frequency Data[J]. Journal of Southwest China Normal University(Natural Science Edition), 2020, 45(3): 73-79. doi: 10.13718/j.cnki.xsxb.2020.03.012
Citation: Chuan-ju QU, Jiao-ping YANG. On Arbitrage Strategy of Stock Index Futures Based on Wavelet De-Noising and Co-Integration Theory for High Frequency Data[J]. Journal of Southwest China Normal University(Natural Science Edition), 2020, 45(3): 73-79. doi: 10.13718/j.cnki.xsxb.2020.03.012
shu

On Arbitrage Strategy of Stock Index Futures Based on Wavelet De-Noising and Co-Integration Theory for High Frequency Data

  • 1.

    Business College, Qingdao Hengxing University of Science and Technology, Qingdao Shandong 266042, China

  • 2.

    School of Economics and Management, Qingdao University of Science and Technology, Qingdao Shandong 266042, China

More Information
  • Received Date: 11/09/2019
    Available Online: 20/03/2020

  • MSC: F830.59;TP301.6

  • In recent years, high-frequency trading (hft) strategy has become a hot topic in the investment field because of its huge profitability. This paper analyzes the potential arbitrage opportunity of stock index futures contract on the first day of listing and several trading days before delisting, and puts forward the idea of arbitrage according to different time points of the contract. Firstly, wavelet analysis is used to denoise the data, then cointegration theory is used to analyze and model the data, and finally, intertemporal arbitrage is used to calculate the return. The empirical results show that the intertemporal arbitrage of stock index futures using Wavelet de-noising co-integration theory has more arbitrage opportunities and better arbitrage effect than using traditional co-integration theory.
  • 加载中
  • [1] KANG S H, TIWARI A K, ALBULESCU C T, et al.Time-frequency Co-movements between the Largest Nonferrous Metal Futures Markets[J].Resources Policy, 2019, 61:393-398.

    Google Scholar

    [2] YUE Y D, LIU D C, XU S.Price Linkage between Chinese and International Nonferrous Metals Commodity Markets Based on VAR-DCC-GARCH Models[J].Transactions of Nonferrous Metals Society of China, 2015, 25(3):1020-1026.

    Google Scholar

    [3] CHUI C K, LIAN J A.A Study of Orthonormal Multi-wavelets[J].Applied Numerical Mathematics, 1996, 20(3):273-298.

    Google Scholar

    [4] DAUBECHIES I.Orthonormal Bases of Compactly Supported Wavelets[J].Communications on Pure and Applied Mathematics, 1988, 41(7):989-996.

    Google Scholar

    [5] 黄彩霞, 陈家新.基于小波系数区域相似度的医学图像融合[J].计算机应用研究, 2008, 25(1):274-276.

    Google Scholar

    [6] 刘柏年, 皇群博, 张卫民, 等.集合背景误差方差中小波阈值去噪方法研究及试验[J].物理学报, 2017, 66(2):89-97.

    Google Scholar

    [7] 王晶.基于VMD分解和小波阈值的语音信号去噪[J].软件导刊, 2017, 16(10):12-14, 18.

    Google Scholar

    [8] 刘晓凰, 李春英.基于EEMD分解和改进小波阈值降噪的齿轮故障诊断[J].机械管理开发, 2018, 33(4):76-78.

    Google Scholar

    [9] LI B Y, LI Y X, WANG H T, et al.Compensation of Automatic Weighing Error of Belt Weigher Based on BP Neural Network[J].Measurement, 2018, 129:625-632.

    Google Scholar

    [10] 张海.基于小波分析的气候要素长时间序列分析[D].北京: 中国地质大学(北京), 2018.

    Google Scholar

    [11] 刘向丽, 王旭朋.基于小波分析的股指期货高频预测研究[J].系统工程理论与实践, 2015, 35(6):1425-1432.

    Google Scholar

    [12] 蒋晓宇, 沈瑶.大宗商品期货市场关联性与价格发现功能研究——基于有色金属国际与国内期货价格的比较分析[J].价格理论与实践, 2015(6):76-78.

    Google Scholar

    [13] 徐国祥, 李文.基于中国金属期货价格指数的价格发现能力实证研究[J].统计研究, 2012, 29(2):48-57.

    Google Scholar

    [14] 隋新玉.基于新型经济指数对我国宏观经济景气状况的研究[J].价格理论与实践, 2018(3):91-94.

    Google Scholar

    [15] 徐照宜, 蒋文倩, 杨胜刚.国际黄金和原油价格波动与上证指数的相关性——基于小波分析方法的研究[J].金融论坛, 2019, 24(6):54-61.

    Google Scholar

    [16] 李冰娜, 惠晓峰, 李连江.基于蒙特卡洛RMT去噪法小股票组合风险优化研究[J].管理科学, 2016, 29(2):134-145.

    Google Scholar

    [17] 李锦成.中国影子银行与股票市场的动态结构相关性——基于小波分析法的实证分析及金融风险防控启示[J].西部论坛, 2018, 28(4):77-85.

    Google Scholar

    [18] 严骏宏.基于离散小波分解和支持向量机的股指组合预测[J].统计与决策, 2017(3):168-171.

    Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(6)  /  Tables(6)

Export Citation
PDF
XML

Article Metrics

Article views(1104) PDF downloads(139) Cited by(0)

Access History

Other Articles By Authors

On Arbitrage Strategy of Stock Index Futures Based on Wavelet De-Noising and Co-Integration Theory for High Frequency Data

  • Received Date: 11/09/2019
  • Available Online: 20/03/2020

Abstract: In recent years, high-frequency trading (hft) strategy has become a hot topic in the investment field because of its huge profitability. This paper analyzes the potential arbitrage opportunity of stock index futures contract on the first day of listing and several trading days before delisting, and puts forward the idea of arbitrage according to different time points of the contract. Firstly, wavelet analysis is used to denoise the data, then cointegration theory is used to analyze and model the data, and finally, intertemporal arbitrage is used to calculate the return. The empirical results show that the intertemporal arbitrage of stock index futures using Wavelet de-noising co-integration theory has more arbitrage opportunities and better arbitrage effect than using traditional co-integration theory.

    HTML

  • 2019年开春以来中国的金融市场开始出现“牛市”迹象，股票指数冲破3000点，以股票指数为标的的股指期货市场出现繁荣景象.中国金融市场的繁荣给投资者的投资增强信心，同时金融数据波动大所带来的风险也不可避免.随着国内市场有效性增强，套利机会稍纵即逝.所以，在牛市环境中如何构建风险可控，收益更高的套利策略一直是金融学术界关注的热点话题.

    以往诸多国内外学者对跨期套利的研究，主要集中在采用传统理论进行跨期套利.一部分学者采用GARCH模型进行期货跨期套利并证明其行之有效性[1-2]；另一部分学者采用统计套利方法进行期货跨期套利；还有一部分学者运用协整理论进行期货跨期套利并证明套利策略的有效性.作为挑战传统学术研究界的新型前沿课题，以小波分析理论等为代表的复杂非线性金融物理学越来越受到主流金融学界的关注[3-6]，国内学者运用小波分析研究中国的金融市场成果较多[7-10].运用小波分析对我国金融市场的研究主要集中在：股票市场价格预测功能，宏观经济时间序列预测[11-15]等，对小波分析法应用于金融投资实际操作的研究较少[16-18].本文在小波理论基础上研究股指期货1分钟高频数据去噪后进行择时套利.

1.   理论基础

    1.1.   小波去噪方法

  • 小波去噪方法是通过小波变换对不同频率信号进行运算分解，并通过分解得到的系数与噪声形成不同强度的分布特征，然后对每个频带上噪声对应的小波系数进行去噪，对原始信号的小波分解系数保留，重构去噪后的系数，得到纯净信号.假设给定信号的f(t)满足一定的条件：f(t)绝对可积.

    则其Fourier变换公式为

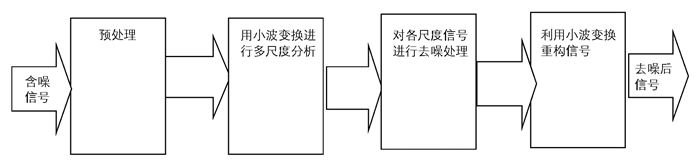
    我们经过傅立叶变换对信号所在域进行改变，对时域信号空间和频域信号空间进行变换.小波去噪步骤如图 1所示.

    小波去噪的关键是在第3步中对每个尺度的小波系数进行去噪.

    小波阈值去噪方法的实现步骤为：①将原始信号傅立叶变换成小波域；②对包含随机噪声的较小小波系数进行阈值处理；③重构去噪后的小波系数.

    阈值处理方法分为硬阈值方法和软阈值方法，其中硬阈值方法更能保留更多原始数据的特征.

    硬阈值函数表达式为

    软阈值函数表达式为

    其中λ表示阈值. sgn为符号函数.

    • 1.2.   协整理论

  • 协整理论是一种研究非平稳时间序列是否存在结构性长期关系的理论.

    对于2个变量而言，协整的定义如下：

    假设有2个时间序列yt和xt是一阶单整过程，如果存在一个非零的β，使得yt与βxt是一个平稳过程I(0)，则称yt和xt之间存在协整关系.其关系式为

    式(4)中，当μt的均值为零的I(0)过程时，则称yt和xt之间存在协整关系.

    在对可能存在相关性的金融时间序列进行协整检验时，首先要对两者之间进行协整性检验.本论文中采用Johansen协整检验法，因为该方法能更全面地检验金融时间序列.

2.   数据处理及建模

    2.1.   数据选取

  • 沪深300股指期货在同一交易日内同时存在当月、下月以及之后2个季月共4份合约.本文研究的是合约上市首日和退市前一周的数据，当月合约交易量最大，所以本文选取当月合约IF1903上市首日和退市前7天的1分钟高频数据和下月IF1904相对应的1分钟高频数据作为研究样本.数据全部来源于Wind(万德)数据库，有效数据共1 120对数据.选取前720对样本作为训练数据，后400对样本作为检验数据.

    • 2.2.   数据相关性分析

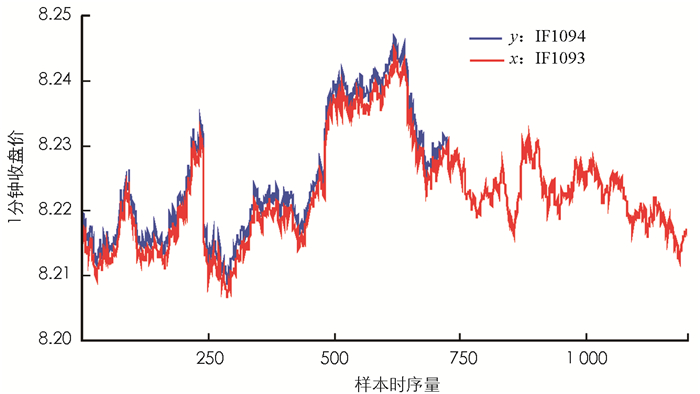
  • 图 2为合约IF1903和IF1904的走势图.通过观察图 2，从趋势上看两份合约的走势大致吻合，由此可初歩推断两合约的相关性比较强.这说明合约IF1903和IF1904的依赖性很强.

    • 2.3.   数据平稳性检验

  • 对两份样本合约数据进行ADF检验，样本数据进行二阶差分处理数据平稳.结果如表 1.

    合约IF1903的ADF=-16.507 76，由显著性可知IF1903序列是平稳性的，合约IF1904的ADF检验，得到ADF=-21.816 36，由显著性可知IF1904序列是平稳的.通过上面的检验，得到的结论是：在1%的显著性水平下，合约IF1903和IF1904的二阶差分序列全都拒绝了原假设.因此，合约的原始时间序列符合二阶单整的标准.

    • 2.4.   小波去噪分析

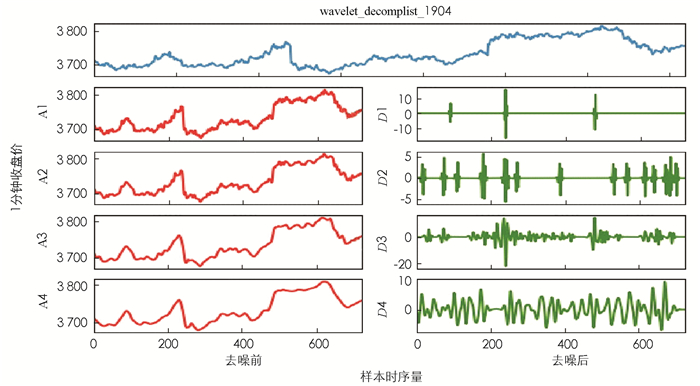
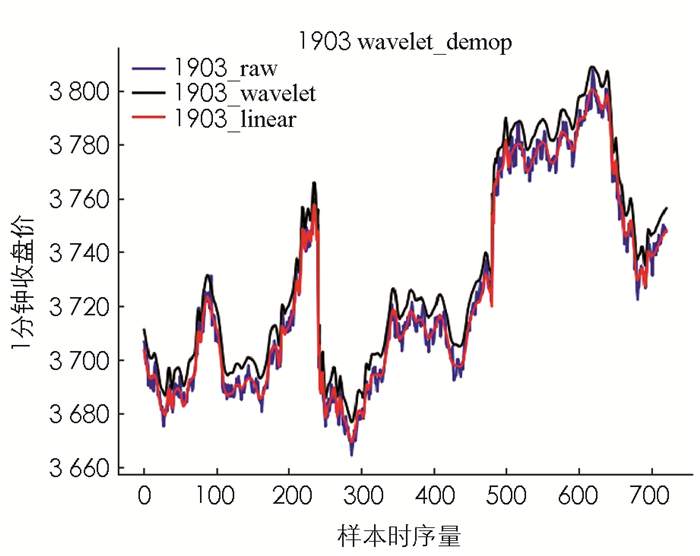
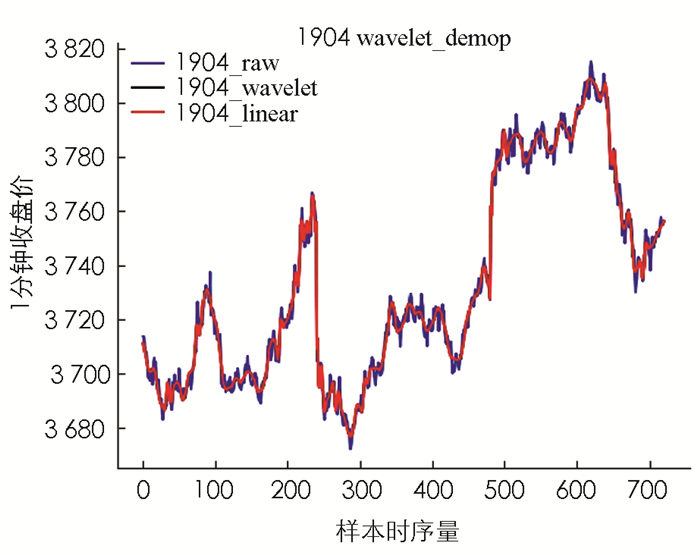
  • 在简单数据处理之后，对数据进行小波去噪.本文最终采用MATLAB中的wden函数，具体操作语句为：wden(data，minimaxi，h，one，4，sym8).其中“data”表示原始数据；“minimaxi”表示选择的阈值标准是极值阈值原则；“h”表示选择的是硬阈值. “one”表示的是阈值处理不受噪声的影响；“4”表示分解层次为4层；“sym8”表示采用sym8小波函数. 图 3和图 4是去噪前后的数据对比图，可以看出去噪后的数据曲线图更加平滑.

    图 5和图 6分别是IF1903和IF1904去噪前后的对比图，可以发现去噪后走势和去噪前走势一致，去噪后更加平滑.

    • 2.5.   协整关系检验

  • 合约IF1903和IF1904的时间价格序列满足二阶单整的要求，通过协整检验，第一步是应用OLS法对两个时间序列建立回归方程，之后利用单位根检验方法对回归方程残差的平稳性进行检验.结果见表 2：

    通过表 2可以观察到，模型拟合优度为0.982 988，调整可决系数是0.982 974.然后再观察表 2中的其他指标，可以判断在拟合优度方面该模型比较好.接下来通过平稳性检测回归序列的残差项.

    表 3为IF1903和IF1904序列方程残差ADF检验结果，在残差序列的ADF检验结果中，通过表 3中数据得到ADF=-15.747.由显著性可知残差序列是平稳的.

    表 4对残差进行Johansen Cointegration Test协整检验，两检验统计结果P值都小于1%水平，因此参差不存在ARCH效应的原假设不成立，条件异方差性存在于残差序列中.

    • 2.6.   EGARCH建模

  • 由于EGARCH模型要求的参数较少，并且大量研究已经得出，在估计或预测金融时间序列数据的波动性和相关性方面采用EGARCH模型比较科学.同时EGARCH(1，1)模型很适合应用于我国资本市场股权价值波动率的研究中.本文应用EGARCH(1，1)模型来刻画条件异方差，样本内数据用EVIEWS软件构建的模型方程为

    对样本内数据进行EGARCH建模得到表 5中数据.

    所以可以得到样本外的参差方程为

    将样本外的数据代入上式，通过计算得到样本外数据的实时参差值，也就是所谓的实际价差.

    • 2.7.   确定阈值及跨期择时套利策略具体操作

  • 在阈值设置过程中，本文假设样本数据服从正态分布，利用SPSS选取样本正态分布图中不同的分位数作为建仓阈值、平仓阈值和止损阈值.本文设置建仓阈值δ1=1.466 0(标准正态分布90%分位数，保证在下一日90%的概率套利交易不亏本)，平仓阈值δ2=0.205 0(16%分位数)，止损阈值δ3=2.321(99.9%分位数).由于实证研究只涉及1份合约，除交易成本外的其他成本比较小，所以在跨期套利实证分析中只考虑交易成本.

    本文采取的套利策略为：当实际价差偏离理论价差，并且出现实际价差大于理论价差时，这里表现为残差δ1大于1.466.此时进场做多远月合约，做空近月合约，即买入远月，卖出近月合约.随着时间对价格的纠正，当实际价差第一次反向且δ2大于0.205 0时，做相反的套利交易，平仓出场.若实际参差不收敛，δ3大于2.51时，则立即平仓出场减少可能造成的损失.当实际价差小于理论价差时，即δ1小于-1.466时，做多近月做空远月合约，即买入近月合约，卖出远月合约.然后，当实际参差第一次反向且δ2小于-0.205 0时，平仓出场.若实际参差不收敛，δ3小于-2.51时，则止损出场.

    通过计算得到样本内数据跨期择时套利日收益率为8.6%，将样本外数据进行回测验证，日收益率为8.5%，模型对样本外数据适用.

    本文对小波去噪后协整理论与传统的协整理论进行跨期套利比较分析(表 6)，实证结果表明采用传统的协整理论进行跨期择时套利日收益率为8.1%.

3.   结语

  • 随着对金融时间序列数据的深入研究，很多研究成果证明金融时间序列数据常常具有非平稳性和非线性性的特征，数据波动较大.金融时间序列数据存在较多的奇异点，同时小幅波动比较频繁，随机性特征明显.因此，对随机性特征明显的时间序列数据研究之前可以进行相应的去噪处理.时间序列数据在时域和频域2个方面通过小波分析反映同一个时间序列的变化，通过小波分析法使时间序列数据在低频细节部分具有较高频率分辨率和较低时间分辨率的特征.同时，在高频逼近部分的特征与低频部分相反.因此，小波分析法处理经济时间序列信号既能保留原始数据的特征，又能达到去噪的目的.本文主要介绍小波去噪法在金融时间序列中的应用，对沪深300股指期货时间序列数据小波去噪后采用协整理论进行分析，然后用EGARCH建模进行跨期择时套利活动，实证分析得到的日收益率比传统的协整理论进行跨期择时套利收益率高.

Figure (6)  Table (6) Reference (18)

Catalog

    Copyright Journal of Southwest China Normal University(Natural Science Edition)

    Address： Tel：023-68252540，68254576，68254478 E-mail：xbbjb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return