-
预应力撑杆柱包括细长的柱和为柱提供有效横向弹性支撑的撑杆以及拉索系统,该结构体系越来越多地被用作提高普通钢柱的稳定性,在国内外的工程实践中被广泛应用.自60年代以来,预应力撑杆柱的研究便已展开. 70年代之后,国内外便有大量的研究人员投入该结构的研究,并且产生了许多研究成果. Hafez基于微小变形假设的理论对单层预应力水平撑杆柱的拉索初始预应力和屈曲荷载的关系进行推导,定量检验了拉索预应力对屈曲载荷的影响[1].为了确保安全性,后续的研究工作中将结构的相关屈曲纳入研究内容.首次对单层四方向预应力水平撑杆柱与单层三方向预应力水平撑杆柱的相关屈曲进行了研究[2-3],表明了相关屈曲对于最大承载力较低的结构起着至关重要的影响.刘学春、许可冉等人对高性能钢材的单层预应力撑杆柱展开了研究,该研究表明通过提高钢材强度,从而提高预应力撑杆柱的承载能力[4].除了对单层撑杆结构的相关屈曲研究外,双层预应力水平撑杆柱的相关屈曲研究也不断深入,结果表明此类双层撑杆结构可忽略相关屈曲影响[5].随着研究的深入,各种结构类型的预应力撑杆柱被研究且运用,在需要细长柱支撑或塔架的地方以及大跨度空间结构可以找到这种结构的实际应用[6].以上研究大多针对撑杆水平布置的情形展开,并未考虑到撑杆类型的多样性.而本文以采用撑杆斜向布置的预应力支撑柱为研究对象,着重于这类结构中的拉索初始预应力分析.
HTML
-
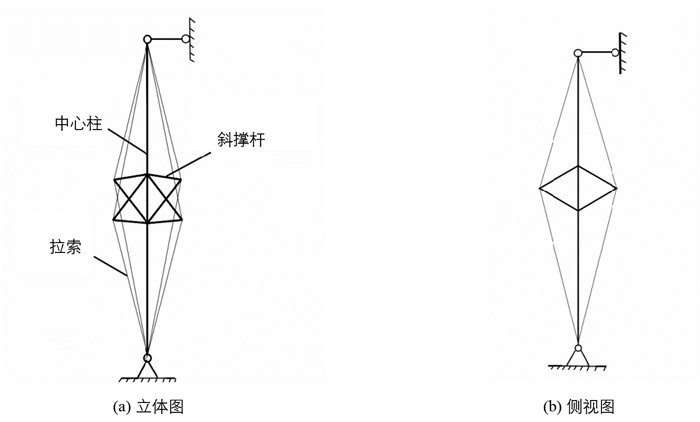
如前所述,本文以撑杆斜向布置的预应力撑杆钢柱为研究对象,其体系构成如图 1所示.其中撑杆在柱身平面内斜向布置,而在垂直柱身平面内正交布置,在预张力索的作用下撑杆对中心柱起到侧向支撑作用.
对预应力撑杆钢柱而言,拉索初始预应力是影响其稳定性能的重要因素,合理设置拉索初始预应力也是准确评估其稳定性能的前提.在进行预应力公式推导时,只在柱身与一组撑杆形成的平面内分析,并基于小变形假设的理论,可以得到预应力斜撑杆柱的平面几何计算简图(图 2).本文在推导初始预应力的计算公式时,提出以下假设:
1) 撑杆与中心柱之间的连接方式为刚接;拉索与撑杆之间的连接方式为铰接.
2) 该结构为完全对称结构并且为轴心受压结构.
如图 2所示,Ti为拉索的初始预应力,P1i为上段柱由于拉索初始预应力引起的轴力.上段柱中由于索初始预应力引起的轴力为
上式中的常数项为撑杆的组数,本次研究的结构为4组撑杆,所以在计算式前会有常数项出现.在图 2中,γ表示拉索与中心柱之间的夹角;β为撑杆与中心柱之间的夹角.
在轴向外荷载P的作用下,中心柱的轴力发生变化,便会导致拉索应力也随之改变.其中,令施加外荷载后的最终拉索应力为Tf;上段柱的最终轴力为P1f.由此可得:
结构上段柱受外加荷载前后轴力的差值ΔP1为
其次,选取撑杆外端与拉索的交点分析.由于拉索的布置方式在沿着撑杆方向存在分力,所以撑杆由于索初始预应力引起的轴力Fi为
当结构在轴向荷载P作用下,不仅结构拉索中的应力会改变,同时撑杆的轴力也会发生相应的变化.为了区分两种状态下的轴力,令结构在施加外荷载后撑杆的轴力为Ff,Ff可表示为
类似地,下柱段中由于索初始预应力引起的轴力P2i为
当结构在轴向荷载P作用下,下段柱的最终轴力为
结构下段柱受外加荷载前后轴力的差值ΔP2为
当轴向外荷载施作用于结构时,中心柱、撑杆与拉索均会产生小变形.在图 2中实线为结构变形前的形态,虚线部分表示结构变形后的形态.通过平面几何分析,在轴向荷载作用下索长的变化、撑杆水平方向长度变化和上下两段柱自身长度变化的关系可以表示为
其中,Δs为拉索长度的变化;Δc为上下两柱段在轴向荷载的作用下其自身的长度变化;Δm为撑杆在水平方向的长度变化.
而拉索长度变化也可通过拉索应力与拉索刚度Ks之间的关系得到,如式(10)所示:
与上式原理相同,上段柱与下段柱的长度变化也可通过上下两段柱的轴力与它们各自的线刚度得到,如式(11)所示:
Kc1,Kc2分别为上段柱和下段柱的轴向刚度.由于结构上下段柱的长度不同会导致上段柱与下段柱的轴向刚度产生差异.
而撑杆长度变化、撑杆水平方向长度和下段柱长度变化的关系可表示为
在上式中,Δa为撑杆的长度变化;Δx为下段柱长度变化;Δm则为撑杆在水平方向长度变化.而式中的Δx也可由轴力与下段柱的刚度表示:
其中,L2为下段柱的柱长.同理,撑杆长度的变化也可以由撑杆轴力与撑杆线刚度Ka表示为
将式(13)、(14)带入(12)可得:
将式(10)、(11)、(15)代入式(9)中,可得:
式中,系数C1为
将式(2)、(10)、(11)、(15)式代入式(9)并化简可得:
将上式代入式(2)可得:
式中,系数C2为:
-
在文献[1]中,初始预应力对预应力撑杆钢柱屈曲荷载的影响可分为3个阶段,本文将在此推导区分这3个阶段临界应力Tmin,Topt,Tmax的计算公式.
Tmin是保证结构屈曲荷载大于等于欧拉荷载PE的情况下的最小初始预应力,可由式(21)表示:
其中Ec为柱的弹性模量;Ic为柱的惯性矩;L为柱的长度.
Topt表示当拉索失去张力,同时当屈曲荷载达到最大值Pmax时拉索的初始预应力,即最佳预应力.当拉索预应力为最佳预应力时,拉索中的最终应力刚好为零,根据式(16)可得:
在第二阶段中,初始预应力大于最小有效预应力但小于等于最佳预应力.由式(16)可得到第二阶段结构的屈曲荷载P2可以表示为
Tmax表示在没有任何外加荷载情况下引起结构屈曲的预应力.在第三阶段中,初始预应力大于最佳预应力Topt.在这种情况下,当结构屈曲时拉索的最终应力非零,此时柱中的轴力是施加的荷载与拉索最终应力的竖向分力的总和且达到最大值Pmax,但由于柱中的轴力较大,在拉索中的应力也并不能抵抗中心柱产生较大距离的位移,此时拉索中的应力可由剩余应力Tr表示.由式(2)、(18)可得:
其中Tr表示在结构屈曲的瞬间拉索的剩余应力.且C3与C4的表达式如下:
由式(24)中不难看出较大的初始预应力便会产生较大的剩余应力.由上文提到拉索应力会有竖直分力,并且其分力也是中心柱轴力的一部分.所以当剩余应力越大时,使得结构屈曲时的外加荷载就会越小.当初始预应力足够大时,即使不对结构进行外荷载的施加,同样也会导致结构屈曲,在这种情况下Tr与Ti均可用Tmax表示,并将其带入式(24)中可得:
由上文的分析与式(19)可以得出在第三阶段中结构的屈曲荷载P3为
上文提到在单层四方向斜撑杆结构中,初始预应力与屈曲荷载的关系可分为3个阶段:第一阶段中,当预应力小于Tmin时,屈曲荷载为欧拉荷载PE;第二阶段中,当预应力介于Tmin与Topt之间时,屈曲荷载与预应力的关系是线性正相关的,即P2=Ti/C1;在第三阶段中,预应力介于Topt与Tmax之间,当预应力达到Tmax时,结构的屈曲荷载为零,在该阶段中屈曲荷载与预应力的关系为负相关.
-
前文通过理论推导建立了初始预应力的理论计算公式,本节拟以具体模型研究不同参数对预应力撑杆钢柱最优初始预应力的影响.本节采用的预应力撑杆钢柱模型参数为:中心柱柱长L为3 000 mm;中心柱和撑杆均为圆管,内、外径分别为25.4 mm和38.1 mm,弹性模量均为201 kN/mm2;拉索弹性模量为202 kN/mm2. La为撑杆外端点到中心柱的水平距离,本文分别取值为:150,225,300,375,450 mm;ϕ为拉索直径,分别取值为:1.6,3.2,4.8,6.4,8.0 mm;α为沿撑杆方向与La方向之间的夹角,分别取值为15°,30°,45°,60°.当引入La,ϕ,α之后.每一个La取值可以得到与之对应的Ka值,每一个α取值可以得到与之对应的β值,同理每个拉索直径取值同样可以得到与之对应的Ks值.根据前文推导的初始预应力计算公式,并结合本节采用的模型参数,可以建立初始预应力与撑杆刚度、拉索刚度以及撑杆倾角的关系(图 3).由图 3(a)可以看出,该结构的预应力值随着撑杆刚度的提升而减小,可见撑杆刚度与预应力值为负相关,与之相反,拉索的索径与拉索的刚度成正比.由图 3(b)可得知结构的预应力值随着拉索线刚度的增大而增大,二者关系为正相关.值得注意的是在图 3(c)中,当β由30°变化为75°的过程中,预应力值的变化趋势是先增大再逐渐减小.
-
通过建立预应力斜撑杆柱模型并对其预应力与屈曲荷载的关系以及影响预应力的因素进行分析.结论总结如下:
1) 基于单层四方向预应力斜撑杆柱结构的平面几何分析以及结构中的几何参数和材料参数推导出了该结构类型的预应力计算公式,进而为此类型结构的研究打下了基础.
2) 对于撑杆布置方式为斜撑杆布置方式的结构而言,当初始预应力在最小有效预应力与最佳预应力之间时,预应力与屈曲荷载之间的关系是线性的,并且当预应力足够大时,屈曲荷载并不会随之持续增大,而是当达到最大屈曲荷载时便开始逐渐减小.
3) 对于单层四方向预应力斜撑杆柱而言,其拉索刚度、撑杆刚度、以及撑杆与中心柱的夹角均会对拉索预应力产生影响.当撑杆刚度增大时,拉索预应力随之减小;而拉索刚度对拉索预应力的影响则相反,当拉索刚度不断增大时,拉索预应力均匀增大.值得注意的是当β增大时,预应力呈现出先缓慢增大再减小的趋势.虽然三者对预应力均有不同程度的影响,但拉索刚度对拉索预应力的影响比起其余两个变量更为明显.








 DownLoad:
DownLoad: