On Compound Poisson-Geometric Risk Model with Fixed Risk Investment and Barrier Dividend

假设所有随机过程和随机变量都定义在完备概率空间(Ω，F_t，F，P)上.为了做好准备工作，先给出索赔次数、盈余过程和有界分红策略的数学描述.

定义1 设λ>0，0 < γ < 1，称非负整值随机变量N服从参数为λ和γ的复合Poisson-Geometric分布，如果其矩母函数为

当γ=0时，

此时，复合Poisson-Geometric分布退化成一般的Poisson分布.

定义2 设λ>0，0≤γ < 1，称随机过程{N(t)}服从参数为λ和γ的复合Poisson-Geometric过程，如果满足：

① N(0)=0；

② N(t)有独立平稳增量；

③ 对任意t≥0，N(t)服从参数为λ和γ的复合Poisson-Geometric分布，且

当γ=0时，复合Poisson-Geometric过程退化为一般的Poisson过程，这里的γ常称为偏离系数.

引理1^[8] 设{N(t)}是服从参数为λ和γ的复合Poisson-Geometric过程，记${\alpha _1}{\rm{ = }}\frac{{\lambda \left( {1 - \gamma } \right)}}{\gamma } $ (若γ=0，则取α₁=λ)，则当t足够小的时候，有$\left\{ \begin{array}{l} P\left( {N\left( t \right) = 0} \right) = {{\rm{e}}^{ - \lambda t}} = 1 - \lambda t{ + _0}\left( t \right)\\ P\left( {N\left( t \right) = k} \right) = {\alpha _1}{\gamma ^k}t + {A_k}{\left( t \right)_0}\left( t \right), k = 1, 2, \cdots \end{array} \right., $其中A_k(t)=γ^k+(k－1)[γ(1+α₁t)]^k－2，且$\sum\limits_{k = 0}^\infty {{A_k}\left( t \right)} $一致收敛.

在本研究的讨论中，都假设索赔计数过程满足复合Poisson-Geometric过程.

设u表示初始资本，$\sum\limits_{i = 1}^{{N_1}\left( t \right)} {{X_i}} $表示保险公司到时刻t为止的累积保费，X_i表示第i次到达的保费额，N₁(t)是参数为λ₁的Poisson过程，表示到时刻t为止保单到达的次数. $\sum\limits_{i = 1}^{{N_2}\left( t \right)} {{Y_i}} $表示保险公司到时刻t为止的累积索赔额，Y_i表示第i次发生的索赔额，N₂(t)是参数为λ₂和γ的复合Poisson-Geometric过程，表示到时刻t为止索赔发生的次数.保险公司还根据初始资本和单位时间内对索赔额的预测来决定投资风险资本，投资额度为F，其价格P(t)满足扩散过程

其中：μ为单位风险收益率，σ为单位风险波动率，W(t)是一维标准布朗运动.则保险公司的盈余U(t)满足改进的复合Poisson-Geometric风险模型

即

其中：N₁(t)，N₂(t)，X_i，Y_j和W(t)相互独立.这里须满足安全负载条件

保险公司考虑以b>0为界，进行有界分红.即当U(t≥b时保险公司将超过b的部分全部进行分红.本研究考虑的红利过程为D(t)，定义${D^{u, b}}\left( t \right) = \int_0^t {{{\rm{e}}^{ - \delta s}}{\rm{d}}} D\left( s \right) $为时刻t的总红利现值.设τ=inf{t≥0：U(t < 0|U(0)=u}为破产时刻，δ≥0为贴现率，则在有界分红策略下，保险公司的盈余为

若策略D^u，b(t)满足P(U^D(t)≥0，∀t≥0|U^D(0)=u)=1，则称其为允许策略，本研究考虑的都是允许策略.

保险公司的期望累积红利现值函数为

首先利用Gerber-Shiu函数的研究方法，研究期望累积红利现值函数V(u；b)所满足的积分-微分方程，最后在贴现率δ=0时得到期望累积红利现值函数V(u；b)的解析解.

设保费额X_i的分布函数为G(x)，概率密度为g(y)；索赔额Y_i的分布函数为F(y)，记F(y)的k重卷积为F^*k(y)，其概率密度F(y)的k重卷积为f^*k(y)，并记${F_\gamma }\left( y \right) = \sum\limits_{k = 1}^\infty {\left( {1 - \gamma } \right){\gamma ^{k - 1}}{F^{*k}}\left( y \right)} , {f_\gamma }\left( y \right) = \sum\limits_{k = 1}^\infty {\left( {1 - \gamma } \right){\gamma ^{k - 1}}{f^{*k}}\left( y \right)} $.

为了证明的方便，先做几个基本工作.考虑在充分小的时间区间(0，t]内，保费和索赔有4种概率.

① 保费的到来和索赔的到来都是0次的概率为

② 保费的到来为0次，而索赔的到来为k(>1)次的概率为

③ 保费到来1次，而索赔的到来为0次的概率为

④ 其他情形下，事件发生的概率为_o(t).

定理1 0≤u≤b时，有

而u>b时，有

证 当0≤u≤b时，在充分小的区间(0，t]内，假设P{u+F(μt+σW(t)) < b}=1，则由盈余过程的马氏性和全期望公式，有

即

其中G(x)=1－G(x).进一步变形，并整理有

由引理1可知：$\sum\limits_{k = 1}^\infty {{\gamma ^k}{f^{*k}}\left( y \right)} , \sum\limits_{k = 0}^\infty {{A_k}\left( t \right){f^{*k}}\left( y \right)} $均一致收敛；由单调收敛定理可知：积分与求和运算可以交换次序.所以有

由文献[10]与^[13]中的理论和方法，给(2)式两端同除以F(μt+σW(t))，并令t→0，有

假设保费额X_i服从参数为α的指数分布，索赔额Y_j服从参数为β的指数分布，则累积索赔额$\sum\limits_{j = 1}^k {{Y_i}} $是服从参数为(k，β)的Gamma分布的，其概率密度为${f^{*k}}\left( y \right) = \frac{{{\beta ^k}}}{{\left( {k - 1} \right)!}}{y^{k - 1}}{{\rm{e}}^{ - \beta y}} $从而不难推导得出，赔付额的概率密度函数为

显然赔付额服从参数为(1－γ)β的指数分布.

定理2 设保费额X_i服从参数为α的指数分布，索赔额Y_j服从参数为β的指数分布，则0≤u≤b时，总期望累积红利现值函数V(u；b)满足微分方程

且满足V(0；b)=0，V′(b；b)=1，V(u；+∞)=0.

证 在定理假设的条件下，为了证明的方便，首先做几个辅助工作.

在(3)式中，先换元，再关于u求导，有

在(3)式中，先换元，再关于u求导，还有

同时还有

对(3)式两边关于求u求导，有

对(4)式两边再关于u求导，有

(3) 式×(1－γ)β+(4)式，有

(4) 式×(1－γ)β+(5)式，有

经换元，再积分，不难得到

结合(8)式，(6)式×(－α)+(7)式有

且满足边界条件

在一般情况下，方程(9)基于边界条件(10)的解析解比较难于求解，但在δ=0时，即贴现率等于零的情形下，V(u；b)表示期望累积红利现值函数，而非期望累积红利现值函数.以下记期望累积红利现值函数为V(u；b)，此时容易得到V(u；b)的解析解.

推论1 当δ=0时，期望累积红利现值函数为

证 当δ=0时，方程(9)为

且满足边界条件V=(0；b)=0，V′(b；b)=1，V(u；+∞)=0.

其特征方程为

不难发现

从而方程(12)的3个根分别为

不难解得，齐次线性微分方程(11)的通解为

其中C₁，C₂和C₃是任意常数.

由于单笔赔付的期望$ \frac{1}{{\left( {1 - \gamma } \right)\beta }}$会大于单笔保费的期望$\frac{1}{\alpha } $，则不难得到$\left( {1 - \gamma } \right)\beta - \alpha \frac{{{\lambda _1} + {\lambda _2}}}{{F\mu }} < 0 $又由于保险公司安全的费率措施应该是单位时间的收取保费的期望$\frac{{{\lambda _1}}}{\alpha } $要大于单位时间赔付的期望$\frac{{{\lambda _2}}}{{\left( {1 - \gamma } \right)\beta }}$, 因此$ F\mu > 0 > \frac{{{\lambda _2}}}{{\left( {1 - \gamma } \right)\beta }} - \frac{{{\lambda _1}}}{\alpha }$由此不难推知$\frac{{{\lambda _2}\alpha + {\lambda _1}\left( {1 - \gamma } \right)\beta }}{{F\mu }} - \alpha \left( {1 - \gamma } \right)\beta ＜ 0 $成立.经过以上分析可得r₁＜0＜r₂成立.再结合文献[6]中的推论1在指数分布的假设下的期望累积红利现值函数的解析解，不难得到C₃=0.再根据边界条件(10)，并解关于C₁和C₂的线性方程组，得到

考虑在复合Poisson-Geometric风险模型中，初始资本u、偏离系数γ、索赔强度λ₂、风险投资额F对期望累积红利现值函数V(u；b)的影响.

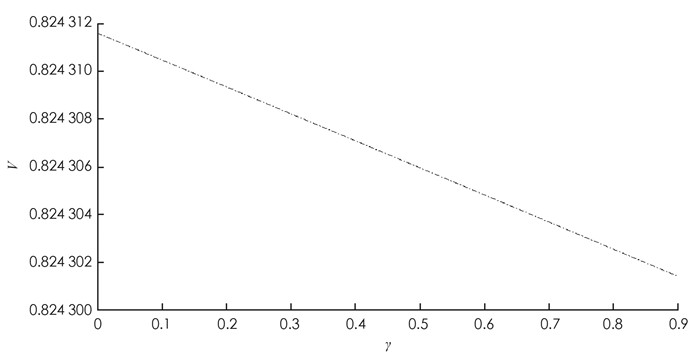
算例1 设初始资本u=50元，保费率λ₁=5份/d，期望保费额$\frac{1}{\alpha } $10元/份，索赔强度λ₂=0.01份/d，期望索赔额$\frac{1}{\beta } $=100元，风险投资额F=30元，单位风险收益率μ=0.15元，分红界b=50元.由函数(13)，利用MATLAB软件得到偏离系数γ与期望累积红利现值函数V(u；b)的关系(图 1).

由图 1可见：红利是偏离系数的减函数，这与文献[12]结论一致.这说明保险公司面对索赔事件时，如果越是持谨慎和保守的态度，设置的赔付门槛越高，偏离系数就越大，此时并不一定能保护盈余水平，提高分红.因此保险公司应该持大度一些的态度，降低赔付的门槛，也就是减小偏离系数，这样反而更会提高分红.

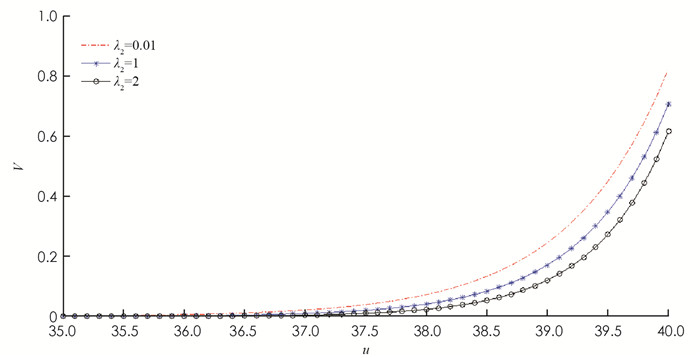
算例2 设保费率λ₁=5份/d，期望保费额$\frac{1}{\alpha } $ =10元/份，索赔强度λ₂=0.01，1，2份/d，期望索赔额$\frac{1}{\beta } $ =100元，偏离系数γ=0.2，风险投资额F=30元，单位风险收益率μ=0.15元，分红界b=40元.由函数(13)，利用MATLAB软件得到初始资本u、索赔强度λ₂与期望累积红利现值函数V(u；b)的关系(图 2).

由图 2可见：红利是初始资本的增函数，这说明保险公司准备比较雄厚的初始资本是增强抗风险能力，提高盈余水平，增加分红的有效手段.同时，索赔事件越是频繁，索赔强度也就越大，风险增加，盈余水平下降，导致分红也会减少，这与文献[12]结论一致.

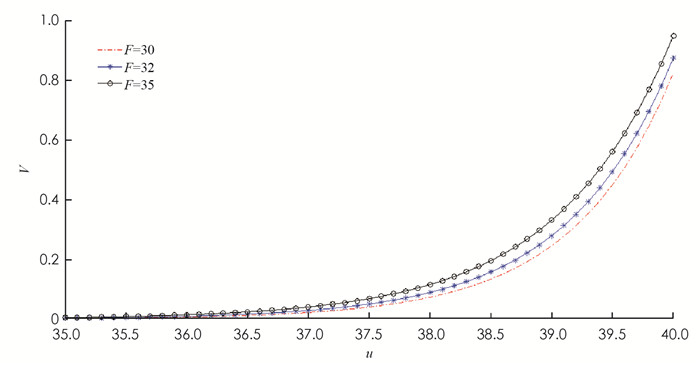
算例3 设保费率λ₁=5份/d，期望保费额$\frac{1}{\alpha } $ =10元/份，索赔强度λ₂=0.01份/d，期望索赔额$\frac{1}{\beta } $ =100元，偏离系数γ＝0.2，风险投资额F=30，32，35，单位风险收益率μ=0.15元，分红界b=40元.由函数(13)，利用MATLAB软件得到初始资本u、风险投资额F与期望累积红利现值函数V(u；b)的关系(图 3).

由图 3可见：红利是投资额度的增函数.风险投资额越多，风险收益越多，保险公司盈余越充裕，从而易于实现分红，且红利也愈多.这说明风险资本投资是提高保险公司盈余水平，增加分红的有效手段.这个结论与文献[11]的结论一致.

通过本节的3个算例发现，并不像直观的感觉那样，越是提高赔付的门槛，保险公司的盈余就会越稳健且越能提高分红；而恰恰相反的，越是持这种保守的赔付态度，则越会降低分红；因此建议保险公司在面对客户的索赔事件时，应当持稍微大度一些的态度，将赔付的门槛设置得适当低一些，这样更有利于提高对股东或者投保客户的分红，同时也有利于提高保险公司的盈余水平，从而既有利于激发客户的投保热情，又能在保费收入上，进一步提高保险公司的盈余水平，从而实现共赢的良好局面.同时，也说明保险公司的风险投资策略对于分红是有利的，适度增加保险公司风险投资额度，也是提高分红，激发投保热情，增加保险公司保费收入和盈余的一种共赢的良好策略.

有别于以往基于随机控制理论的研究，本研究基于Gerber-Shiu函数的全期望思想方法，考虑了一种基于免赔款制度和无赔款保费折扣优待制度的改进复合Poisson-Geometric风险模型的带固定风险投资的有界分红问题，通过使用一定的数学方法，得到了期望累积红利现值函数满足的积分-微分方程，并在δ=0时，得到了期望累积红利现值函数的解析解，最后通过数值算例，分析了偏离系数、索赔强度、初始资本和风险投资额等几个模型参数对期望累积红利现值函数的影响.结合保险实务中的一般经验和认识，提出了保险资金管理的建议和措施.

当然本研究的结果没有找到期望累积红利现值函数与单位风险波动率之间的关系，同时也没有研究该模型下的破产时刻的瞬间盈余与赤字的联合分布，以及破产赤字的Gerber-Shiu函数所满足的更新方程.我们以后将继续在Gerber-Shiu函数上展开研究.