Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2020 Volume 45 Issue 7
Article Contents
Previous Article Next Article

Lei MA, Chang-sheng LI, Jie-rong GUO. Atomic Simulation of Fatigue Crack Propagation at Different Temperature in Ni3Al[J]. Journal of Southwest China Normal University(Natural Science Edition), 2020, 45(7): 55-61. doi: 10.13718/j.cnki.xsxb.2020.07.008
Citation: Lei MA, Chang-sheng LI, Jie-rong GUO. Atomic Simulation of Fatigue Crack Propagation at Different Temperature in Ni3Al[J]. Journal of Southwest China Normal University(Natural Science Edition), 2020, 45(7): 55-61. doi: 10.13718/j.cnki.xsxb.2020.07.008
shu

Atomic Simulation of Fatigue Crack Propagation at Different Temperature in Ni3Al

  • Hunan Province Cooperative Innovation Center for The Construction and Development of Dongting Lake Ecological Economic Zone, Hunan University of Arts And Science, Changde Hunan 415000, China

More Information
  • Received Date: 05/11/2018
    Available Online: 20/07/2020

  • MSC: TG113.25

  • The fatigue crack propagation behavior of Ni3Al at different temperature is simulated by molecular dynamics simulation. The crack models of different initial orientation are constructed to analyze the crack propagation behavior at different temperature. The simulation results show that the mainly deformation mechanisms of the crack tip in Ni3Al are dislocations, slip and void at 400K, and the initial orientation of crack is different, the mode of crack propagation, the deformation characteristics of crack, and the crack propagation rate are differences. When the temperature rises from 400K to 600K, the crack propagation rate of Ni3Al increase with the increasing of temperature. But the high temperature do not change the slip system of the crack tip. However, the number of the initial slip bands decrease at crack tip as the temperature increasing, and the number of slip bands increase in the rapid expansion of crack.
  • 加载中
  • [1] POLLOCK T M, ARGON A S. Creep Resistance of CMSX-3 Nickel Base Superalloy Single Crystals [J]. Acta Metallurgica et Materialia, 1992, 40(1): 1-30. doi: 10.1016/0956-7151(92)90195-K

    CrossRef Google Scholar

    [2] REED R C. The Superalloys [M]. Cambridge: Cambridge University Press, 2006.

    Google Scholar

    [3] MANONUKUL A, DUNNE F P E, KNOWLES D. Physically-Based Model for Creep in Nickel-base Superalloy C263 both Above and Below the Gamma Solvus [J]. Acta Materialia, 2002, 50(11): 2917-2931. doi: 10.1016/S1359-6454(02)00119-2

    CrossRef Google Scholar

    [4] KOLBE M. The High Temperature Decrease of the Critical Resolved Shear Stress in Nickel-base Superalloys [J]. Materials Science and Engineering: A, 2001, 319-321: 383-387. doi: 10.1016/S0921-5093(01)00944-3

    CrossRef Google Scholar

    [5] KOVARIK L, UNOCIC R R, LI J, et al. Microtwinning and Other Shearing Mechanisms at Intermediate Temperatures in Ni-based Superalloys [J]. Progress in Materials Science, 2009, 54(6): 839-873. doi: 10.1016/j.pmatsci.2009.03.010

    CrossRef Google Scholar

    [6] KNOWLES D M, GUNTURI S. The Role of 〈112〉{111} Slip in the Asymmetric Nature of Creep of Single Crystal Superalloy CMSX-4 [J]. Materials Science and Engineering: A, 2002, 328(1-2): 223-237. doi: 10.1016/S0921-5093(01)01688-4

    CrossRef Google Scholar

    [7] SAROSI P M, VISWANATHAN G B, MILLS M J. Direct Observation of an Extended Complex Stacking Fault in the Γ′ Phase of a Ni-base Superalloy [J]. Scripta Materialia, 2006, 55(8): 727-730. doi: 10.1016/j.scriptamat.2006.06.019

    CrossRef Google Scholar

    [8] FLEURY E, RÉMY L. Behavior of Nickel-Base Superalloy Single Crystals under Thermal-Mechanical Fatigue [J]. Metallurgical and Materials Transactions A, 1994, 25(1): 99-109. doi: 10.1007/BF02646679

    CrossRef Google Scholar

    [9] CHIERAGATTI R, REMY L. Influence of Orientation on the Low Cycle Fatigue of MAR-M 200 Single Crystals at 650 ℃ II: Cyclic Stress-strain Behaviour [J]. Materials Science and Engineering: A, 1991, 141(1): 11-22.

    Google Scholar

    [10] KRAFT S, ZAUTER R, MUGHRABI H. Aspects of High-Temperature Low-cycle Thermomechanical Fatigue of a Single Crystal Nickel-Base Superalloy [J]. Fatigue & Fracture of Engineering Materials and Structures, 1993, 16(2): 237-253. doi: 10.1111/j.1460-2695.1993.tb00755.x

    CrossRef Google Scholar

    [11] MOVERARE J J, JOHANSSON S. Damage Mechanisms of a High-Cr Single Crystal Superalloy During Thermomechanical Fatigue [J]. Materials Science and Engineering: A, 2010, 527(3): 553-558. doi: 10.1016/j.msea.2009.08.023

    CrossRef Google Scholar

    [12] KANESUND J, MOVERARE J J, JOHANSSON S. Deformation and Damage Mechanisms in IN792 during Thermomechanical Fatigue [J]. Materials Science and Engineering: A, 2011, 528(13-14): 4658-4668. doi: 10.1016/j.msea.2011.02.063

    CrossRef Google Scholar

    [13] HONG H U, KANG J G, CHOI B G, et al. A Comparative Study on Thermomechanical and Low Cycle Fatigue Failures of a Single Crystal Nickel-based Superalloy [J]. International Journal of Fatigue, 2011, 33(12): 1592-1599. doi: 10.1016/j.ijfatigue.2011.07.009

    CrossRef Google Scholar

    [14] SUN F, ZHANG J X, HARADA H. Deformation Twinning and Twinning-Related Fracture in Nickel-base Single-crystal Superalloys During Thermomechanical Fatigue Cycling [J]. Acta Materialia, 2014, 67: 45-57. doi: 10.1016/j.actamat.2013.12.011

    CrossRef Google Scholar

    [15] ZHOU H, HARADA H, RO Y, et al. Investigations on the Thermo-mechanical Fatigue of Two Ni-based Single-Crystal Superalloys [J]. Materials Science and Engineering: A, 2005, 394(1-2): 161-167. doi: 10.1016/j.msea.2004.11.013

    CrossRef Google Scholar

    [16] DAO M, KAD B K, ASARO R J. Mechanism of Intense Shear Failure in Ni3Al Single Crystals [J]. Philosophical Magazine A, 1997, 75(2): 443-459. doi: 10.1080/01418619708205151

    CrossRef Google Scholar

    [17] 佘连兵, 李信韬, 李扬荣.无界域上非自治Reaction-Diffusion方程的后向紧动力学[J].西南大学学报(自然科学版), 2018, 40(9): 59-66.

    Google Scholar

    [18] XIE H X, WANG C Y, YU T, et al. Dislocation Formation and Twinning from the Crack Tip in Ni3Al: Molecular Dynamics Simulations [J]. Chinese Physics B, 2009, 18(1): 251-258.

    Google Scholar

    [19] XIE H X, BO L, YU T. Atomistic Simulation of Microtwinning at the Crack Tip in L12Ni3Al [J]. Philosophical Magazine, 2012, 92(12): 1542-1553. doi: 10.1080/14786435.2011.652690

    CrossRef Google Scholar

    [20] XIE H X, YU T, YIN F X, et al. The Effects of Crack Orientation on the Twin Formation from the Crack Tip in γ′-Ni3Al [J]. Materials Science and Engineering: A, 2013, 580: 99-104. doi: 10.1016/j.msea.2013.05.048

    CrossRef Google Scholar

    [21] PURJA PUN G P, MISHIN Y. Development of an Interatomic Potential for the Ni-Al System [J]. Philosophical Magazine, 2009, 89(34-36): 3245-3267. doi: 10.1080/14786430903258184

    CrossRef Google Scholar

    [22] MISHIN Y, FARKAS D, MEHL M J, et al. Interatomic Potentials for Monoatomic Metals from Experimental Data Andab Initiocalculations [J]. Physical Review B, 1999, 59(5): 3393. doi: 10.1103/PhysRevB.59.3393

    CrossRef Google Scholar

    [23] HONEYCUTT J D, ANDERSEN H C. Molecular Dynamics Study of Melting and Freezing of Small Lennard-Jones Clusters [J]. The Journal of Physical Chemistry, 1987, 91(19): 4950-4963. doi: 10.1021/j100303a014

    CrossRef Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(8)  /  Tables(1)

Export Citation
PDF
XML

Article Metrics

Article views(1545) PDF downloads(6) Cited by(0)

Access History

Other Articles By Authors

Atomic Simulation of Fatigue Crack Propagation at Different Temperature in Ni3Al

  • Received Date: 05/11/2018
  • Available Online: 20/07/2020

Abstract: The fatigue crack propagation behavior of Ni3Al at different temperature is simulated by molecular dynamics simulation. The crack models of different initial orientation are constructed to analyze the crack propagation behavior at different temperature. The simulation results show that the mainly deformation mechanisms of the crack tip in Ni3Al are dislocations, slip and void at 400K, and the initial orientation of crack is different, the mode of crack propagation, the deformation characteristics of crack, and the crack propagation rate are differences. When the temperature rises from 400K to 600K, the crack propagation rate of Ni3Al increase with the increasing of temperature. But the high temperature do not change the slip system of the crack tip. However, the number of the initial slip bands decrease at crack tip as the temperature increasing, and the number of slip bands increase in the rapid expansion of crack.

    HTML

  • 镍铝单晶高温合金具有优异的高温力学性能, 是制造先进航空发动机等涡轮叶片的主要材料[1-2], 与国防尖端武器和民用产业的技术发展密切相关.在过去几十年里, 研究者们针对镍基单晶高温合金的力学性能进行了大量的研究.研究结果表明, 在低温时镍基单晶合金主要的变形机制为a/2〈110〉位错的剪切过程[3], 然而在高温时微观结构由于刃型位错的运动所产生的微观孪晶是其主要的变形机制[4-7].同时孪晶有两种类型, 一种是由于a/3[112]位错引起的真孪晶, 另一种是由a/6[112]位错引起的伪孪晶.除此之外, 镍铝单晶高温合金在循环加载下疲劳失效也是重要的研究领域.研究发现, 镍基单晶合金的热力学疲劳包括两种不同的变形机制, 一种是低温下的剪切滑移带, 滑移系为{111}〈110〉; 另一种变形机制为高温下的氧化损伤[8-11].同时, 裂纹的扩展行为也受到孪晶形成过程的影响, 所以, 孪晶和裂纹的相互作用在研究镍基单晶合金的裂纹扩展中起着很重要的作用[12-13].一些实验结果还指出, 镍基单晶合金中裂纹的萌发和扩展在最大应变和最低温度时会加快, 并指出在(111)晶面会形成a/6[112]位错, 滑移系为{111}〈112〉系统[14-16].

    镍基单晶合金中的Ni3Al相为强化析出相, 它是L12结构, FCC点阵排列[17].对于析出相断裂强度及裂纹扩展的研究有利于更好地理解镍基单晶合金的力学行为.随着分子动力学方法的发展, 对研究复杂微观结构的演变提供了一种很重要的工具[17], 并且已经应用到Ni3Al裂纹扩展的研究中.如Xie等[18-20]采用分子动力学的方法, 在外部应力的加载下模拟了Ni3Al中裂纹的晶向对裂纹尖端孪晶形成的影响, 模拟的结果表明, (001)〈110〉裂纹的尖端出现了两条滑移带, 然而, (1 10)〈110〉裂纹和(11 0)〈110〉裂纹的尖端产生的是孪晶而不是滑移带, 并且是由裂纹尖端的位错在(111)晶面的发射所形成的, 并且还指出造成孪晶和滑移带的主要原因是裂纹尖端堆垛能和剪切应力.

    本研究采用分子动力学的方法模拟Ni3Al中疲劳裂纹扩展的行为, 分析了裂纹扩展中裂纹尖端微观结构的演变, 并通过裂纹长度的变化和应力强度因子讨论了裂纹扩展速率的变化; 讨论了不同晶向的裂纹对裂纹扩展路径及裂纹尖端微观结构的影响, 并且对比了它们的裂扩展速率及应力强度因子的变化.

1.   模型和方法

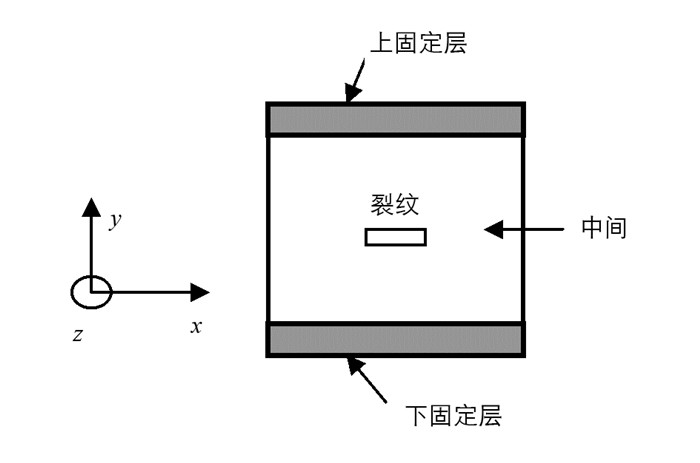
  • 图 1为Ni3Al合金L12结构晶体模型, 晶格常数a=0.353 3 nm, 盒子的长度为100 a×100 a×50 a, 总的原子数为200万个.在模型的中心位置通过删除原子的方法构建一个通透性矩形裂纹, 裂纹的长度c=3.533 nm, 占盒子总长度的1/10.裂纹的方向沿z方向, 裂纹所在的面垂直于y方向, x方向为裂纹正前方的扩展方向.模型在x和z方向上施加周期性边界条件, 在y方向上采用非周期边界条件.其中, 裂纹的表示方法是通过它所在的面和方向来描述的, 如(010)[001]裂纹, 加载方向为[010]方向.为了研究晶向对裂纹扩展行为的影响, 先后又建立不同方向的裂纹模型: (110)[001]裂纹模型和(111)[112]裂纹模型, 加载方向分别是[110]和[111]方向. 图 2为循环加载的方式, 在y方向上采用应变的连续幅值加载, 初始循环加载的应变幅值为0.01, 卸载的比例R=εmin/εmax=0.3.循环加载之前, 所有的裂纹模型都进行分子动力学弛豫, 时间步长为1 fs, 应变率为1×10-9 s-1, 体系在模拟过程中采用NVT系统, 应用Nose-Hoover热浴的方法维持系统的温度, 达到平衡后进行应变的循环加载.

    在分子动力学的模拟过程中, 采用Mishin[21-22]构建的嵌入原子势(EAM)来描述Ni-Al间的相互作用, 应用大规模原子或者分子并行计算(LAMMPS)的分子动力学代码研究疲劳裂纹扩展行为. 表 1给出了通过LAMMPS计算的Ni3Al的基本晶格参数, 计算出来的结果和实验值基本一致.同时应用键对结构分析法[23](CNA)分析裂纹尖端微观结构的演变, 揭示裂纹的扩展机制.

2.   结果与讨论

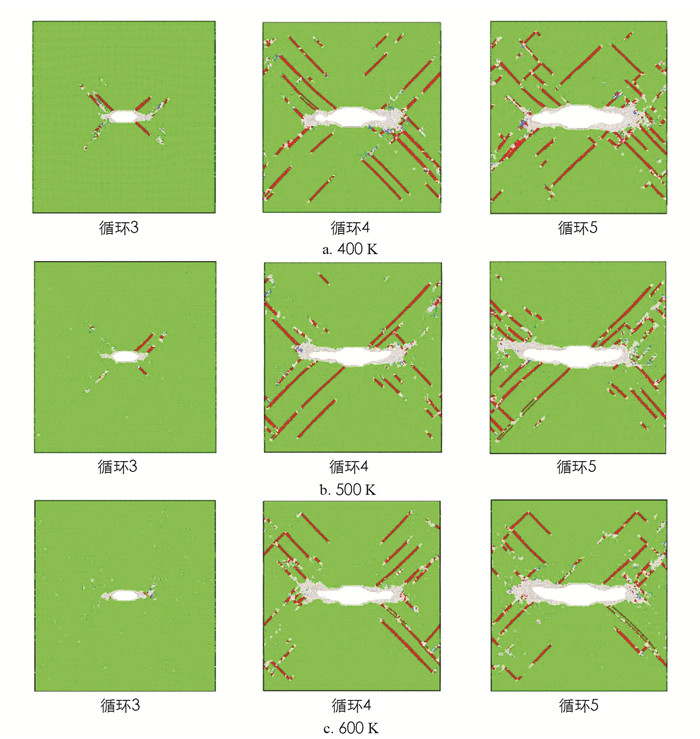
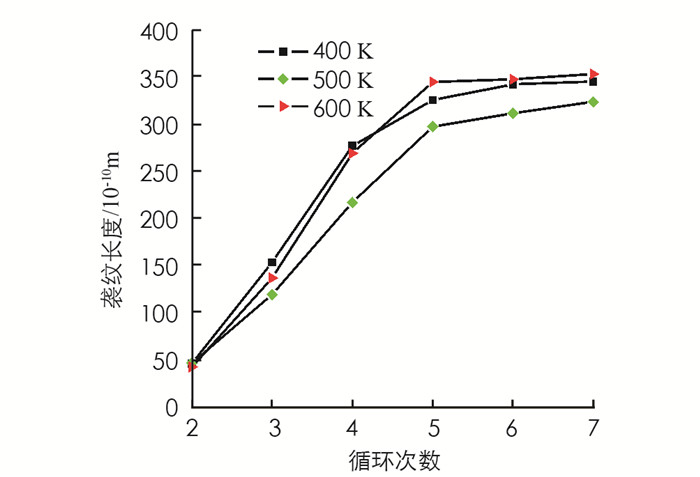
  • 图 3表示不同温度下Ni3Al中(010)[001]裂纹在循环加载下的疲劳裂纹扩展行为. 图 3中绿色代表Ni3Al晶体结构, 裂纹尖端白色为钝化原子, 红色为位错滑移.从模拟的结果可以得到, 裂纹在400 K时(图 3a)从第3个循环开始进行扩展, 裂纹前端出现了钝化效应, 形成了微尖端裂纹, 同时裂纹的周围产生了位错滑移, 这是由于裂纹前端的应力集中比较剧烈需要更多的滑移带来缓解, 其中滑移系统为〈110〉{111}.随着负载的增加, 从第4个循环开始裂纹的尖端开始形成空洞, 然后, 裂纹以微尖端裂纹、空洞以及钝化效应的方式快速地扩展.到了第5个循环时, 裂纹的扩展速率明显加快, 裂纹周围的位错滑移由长程滑移变为短程滑移, 并出现了很多的交叉滑移.从图 3a到图 3c温度由400 K升高到600 K, 随着温度的升高, 裂纹初始的萌发仍然是以微裂纹的形成和钝化效应的产生为主, 但是, 裂纹尖端的位错滑移的数量却在减少, 以至于在600 K时, 裂纹的前端在初始扩展时没有出现塑性变形.这是由于随着温度的升高, 晶体结构变得软化, 内部应力减小, 从而导致裂纹尖端应力集中效应被削弱, 因此, 裂纹周围的塑性变形也就变少了.但是从裂纹长度的变化可以观察到, 裂纹的扩展速率是随着温度的升高而增加的. 图 4计算了裂纹长度在不同温度下随着循环加载次数的变化情况.从图 4中可以得到, 裂纹的长度随着循环加载次数增加而增加, 而且当温度从400 K升高到600 K时, 裂纹的长度也是随着温度的增加而增长的.通过拟合裂纹长度随着循环加载次数的变化曲线(da/dn)就可以得到裂纹的平均扩展速率, 由此可以得到, 从400 K到600 K裂纹平均扩展速率分别为6.4×10-10, 6.58×10-10和6.78×10-10m.从这些数据也可以推断出: (010)[001]裂纹的扩展速率从400 K到600 K是增加的.

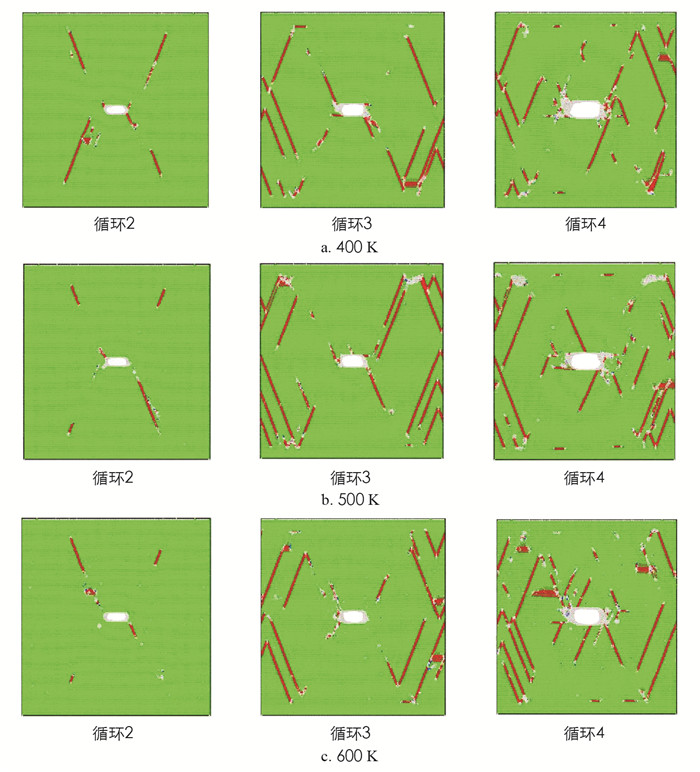
    图 5给出了Ni3Al中(110)[001]裂纹在不同温度下的疲劳裂纹扩展行为以及尖端微观结构的演变.从400 K到600 K, 裂纹在初始扩展时, 裂纹前端的变形机制出现了不同, 在400 K时, 裂纹的前端主要出现了位错滑移, 但是随着温度的升高, 裂纹前端的位错越来越少, 最后裂纹尖端的变形机制只剩下钝化效应了, 这和(010)[001]裂纹在不同温度下的扩展特点类似, 也是由于高温时系统软化引起的.从第3个循环开始, 裂纹扩展速率加快, 在裂纹的扩展过程中周围的滑移带也出现了, 同时在裂纹的前端还出现了部分的BCC相变(图 4中蓝色区域表示), 这是在常温下没有的变形机制.到了第4个循环, 裂纹尖端的塑性变形开始逐渐消失, 裂纹进入快速扩展阶段. 图 6计算了Ni3Al中(110)[001]裂纹长度在不同温度下随着循环加载的变化情况.从图 6中观察到, 在400 K和500 K时, 裂纹长度的变化几乎相同, 而600 K时, 裂纹长度的变化明显低于400 K和500 K.通过拟合得到(110)[001]裂纹从400 K到600 K的平均扩展速率分别为6.0×10-10, 5.9×10-10, 6.45×10-10 m.由此可以得到, (110)[001]裂纹在400 K和500 K时平均扩展速率比较接近, 到了600 K时裂纹扩展速率最大.

    图 7为不同温度下Ni3Al中(111)[112]裂纹在循环加载下的疲劳裂纹扩展行为.从模拟的结果可以得到, 从400 K到600 K, 裂纹初始扩展时尖端的变形机制主要为位错滑移和钝化效应, 并且裂纹尖端的滑移系和常温下的滑移系相同.但是, 不同温度下裂纹尖端的形变特点不同, 在高温时裂纹尖端的钝化区域更大一些, 滑移带的密度也比常温时大很多, 裂纹的宽度和长度明显增大. 图 8计算了Ni3Al中(111)[112]裂纹尺寸在不同温度下随着循环加载的变化情况.从图 8中可以得到, 从400 K到600 K, 裂纹扩展时的平均扩展速率分别为3.01×10-10, 2.75×10-10, 2.6×10-10 m, 从数据中可以得出, (111)[112]裂纹在400 K时裂纹扩展速率达到最大值, 然而在500 K和600 K时, 出现了降低.然后通过对比(010)[001]裂纹和(110)[001]裂纹的裂纹扩展行为, 由于(111)[112]裂纹存在两个不同的滑移系, 裂纹周围的塑性更好, 从而对裂纹的扩展限制比较多, 因此, (111)[112]裂纹在Ni3Al合金中有最小的扩展速率.

3.   结论

  • 研究了温度对Ni3Al疲劳裂纹扩展行为的影响.从400 K到600 K, Ni3Al中裂纹的扩展速率随着温度的升高而增加, 与裂纹的初始取向无关, 而且高温没有改变裂纹前端的滑移系统.在不同取向的裂纹中, 裂纹扩展时在高温不仅出现了钝化效应, 而且还形成了微尖端裂纹, 同时, 裂纹的周围出现许多位错滑移, 这是由于裂纹前端的应力集中, 比较剧烈, 需要更多的滑移带来缓解而引起的.但是随着温度升高, 裂纹尖端的初始位错滑移的数量却在减少, 以至于在600 K时, 裂纹的前端在初始扩展时没有出现塑性变形, 这是因为随着温度的升高, 裂纹在初始扩展时内部应力减少, 晶体结构变得软化, 从而导致裂纹尖端应力集中效应被削弱, 所以裂纹周围的塑性变形也就变少了, 但是裂纹在快速扩展过程中, 滑移的数量随着温度的升高而增加.

Figure (8)  Table (1) Reference (23)

Catalog

    Copyright Journal of Southwest China Normal University(Natural Science Edition)

    Address： Tel：023-68252540，68254576，68254478 E-mail：xbbjb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return