On Barycentric Rational Interpolation Collocation Method to Solve 1D and 2D Convection Diffusion Equation

重心有理插值配点法是根据重心Lagrange插值法改进权值得到的，权值的合理性直接影响数值的逼近精度和稳定性.用重心有理插值配点法求解对流扩散方程最关键的步骤是对微分方程的离散^[17]，离散前需构造出重心有理插值的微分矩阵，即明确待求函数与插值基函数值之间的函数关系.若给定n个离散点，记为x₁，x₂，…，x_n，任选一个整数d，且满足0≤d≤N，J_k={i：i=k－d，…，k}，则重心有理权为

对于区间[a，b]上的n个节点a=x₁ < x₂ < … < x_n=b，函数u(x)在节点处的函数值为u_j=u(x_j)(j=1，2，…，n)，则函数u(x)的重心有理插值函数为

其中B_j(x)为

移项后，将公式(2)两边同时乘以x－x_i(i≠j)，令L_j=B_j(x)，变形后得

对(3)式两边分别关于x求一阶和二阶导数，同时记

则有

然后，将s′(x_i)，s″(x_i)的结果分别代入(4)，(5)式，可得

一维重心有理插值的一、二阶微分矩阵的元素计算公式分别表示为

再用数学归纳法依次可得m阶微分矩阵的元素计算公式为

u(x)在节点x₁，x₂，…，x_n对应的函数向量为u =(u₁，u₂，…，u_n)^T，则一维m阶导数的离散公式为

D^(m)为未知函数u (x)的m阶微分矩阵，记为u ^(m)= D ^(m) u.二维偏微分方程的离散公式是在一维的离散基础上形成的，在表示二维重心有理插值微分矩阵的同时还需要引入Kronecker积，C ^(l)，D ^(k)表示沿着x方向和y方向的l，k阶微分矩阵，且规定C ⁽⁰⁾= I _M，D ⁽⁰⁾= I _N，其中I _M，I _N为单位矩阵.对二维l+k阶偏导函数u ^(l，k)(x_i，y_j)(i=1，2，…，M；j=1，2，…，N)，离散的结果为

已知P_n(x)是重心插值函数，${\hat P_n}(x)$是考虑了微小扰动后的函数逼近值.由误差摄动理论来估计最后的误差范围，也是对数值舍入误差敏感度的衡量.向后误差分析有助于检验算法在计算过程中的稳定性.当计算的扰动项ε很小时，若求解的数值结果在误差允许的范围内，则算法是向后稳定的.估计时引入函数的条件数来表示扰动的灵敏度.由文献[18]中的定理4.1可得相对误差估计界为

定理1   若使用第二类Chebyshev插值点，P_n(x)是重心Lagrange插值函数，P^*(x)是f(x)的最佳一致逼近多项式^[19]，则存在常量$C = \frac{2}{\pi }\log n + 2$，使得

定理2   若使用等距节点做为重心插值逼近的离散点，则满足如下范数关系式：

其中Λ_n为Lebesgue常量，也是有上下界的^[20].

定理3   影响重心有理插值算法收敛性的主要因素有多项式r_n(x)的次数d以及网格尺寸h^[21].假如d≥1，n≥3，并且f∈C^d+2[a，b]，最大网格步长为$h = \mathop {\max }\limits_{0 \le i \le n - 1} ({x_{i + 1}} - {x_i})$，当h→0时，重心插值的收敛阶为O(h^d+1)，且满足不等式

本算例求解的是一维非定常对流扩散方程，采用等距节点对方程进行离散，并将本文的重心有理插值配点法与文献[22]中的3种有限差分法进行比较.差分格式包括了古典隐格式、C-N格式、高精度紧致差分格式，3种有限差分数值解格式中表现较好的是高精度紧致差分格式，待求解方程为

初始条件：u(0，t)=0，u(1，t)=e^－tsin 1，t∈[0, 1].

边界条件：u(x，0)=sin x，u(x，1)=e^－1sin x，x∈[0, 1].

解析解：u(x，t)=e^－tsin x，x∈[0, 1]，t∈[0, 1].源项函数为f(x，t)=te^－tsin xcos x，对流系数为P(x，t)=tsin x，扩散项系数ε=1.用重心有理插值配点法对方程(14)进行离散，有

其中：D_t⁽¹⁾是关于时间项的一阶微分矩阵，D _x⁽¹⁾是空间项x的一阶微分矩阵；同理，二阶微分矩阵为D _x⁽²⁾，源项函数(右端项)是列向量F _c.边界条件属于Dirichlet边界，初始条件的离散结果为I _t u _t= F ₁，边界条件的离散结果为I _x u _x= F ₂，使用附加法将控制方程与初边值条件的离散结果组装，形成一个总的线性方程组A _L U = F.求解结果如表 1所示，空间步长参数为h，时间步长定为τ=0.05，数值结果都是在同一网格尺度下进行比较的.

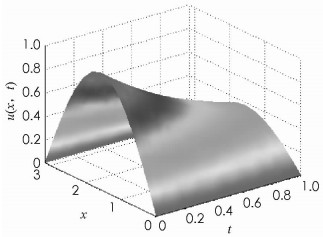
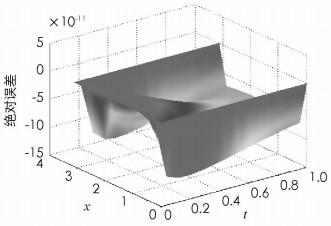
通过以上数值实验对比，在3种有限差分格式中，高精度紧致差分格式求解的逼近精度相对较高，但是与重心有理插值配点法相比，高精度紧致差分格式的逼近精度以及收敛速度明显较低.重心插值配点法的空间步长不需要划分到很细便能达到理想的逼近结果，该数值结果也能反映出重心插值配点法的优势所在.此外，算例1数值结果的可视化如图 1与图 2所示，图 1是重心有理插值的数值解，呈现出了非常光滑的曲面性质. 图 2则是$h = \frac{1}{{32}}$时的绝对误差图，误差图在边界波动较大，内部变化相对平缓，说明对流扩散类方程在使用重心插值配点法求解时，边界处的离散点选取非常重要.

本算例同样取的是一维非定常对流扩散方程，不同之处在于采用了两种离散点进行求解，分别是等距节点与Chebyshev离散点.本算例另一个区别是采用了Robin边界条件，初始条件中出现了函数的偏导，再按照重心有理插值理论对方程进行离散，待求解的一维非定常对流扩散方程为

初始条件：${u_x}(0, t) - \frac{3}{2}u(0, t) = 0, u(1, t) + u(1, t){\rm{ = }}2t{e^{1 - \beta t}}t \in [0, 1].$

边界条件：u(x，-1)=(x²-1)e^x+β，u(x，1)=(1-x²)e^x-β，x∈[－1，1].

解析解：u(x，t) = (1-x²)te^{x-β t}，x∈[－1，1]，t∈[0, 1].

源项函数：$f(x,t) = \frac{1}{2}{{\rm{e}}^{x - \beta t}}(1 - \beta t + {x^2} - \beta tx - 2t - 2tx)$.

扩散项系数为$P(x) = \frac{1}{{x + 3}}$，对流项系数为$Q(x) = -\frac{1}{{x + 1}}$.方程离散结果为

边界条件的离散结果表示为I _m u₁= F ₁，t=0，x∈[-1, 1]，与I _m u₂= F ₂，t=1，x∈[-1, 1].另外2个初始条件的离散结果为[D _x⁽¹⁾⊗ I _n－1.5 I _n] u₃= F₃和[(D _x⁽¹⁾⊗ I _n)+ I _n] u₄= F₄.组装成总的离散方程后可以得到A _L U = F，其中U =(u，u₁，u₂，u₃，u₄)^T，F =(F _c，F₁，F₂，F₃，F₄)^T，求解数值结果如表 2所示.

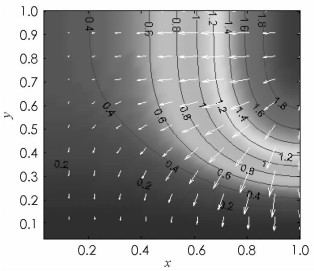
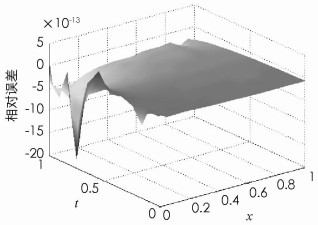
表 2中的E₁与E₂分别代表了参数β=0.5与β=1的相对误差.从结果可以看出参数β的选取对数值结果是有影响的(限于篇幅，其他的β数值未一一列举).数值结果中得到的规律是：随着参数β的增大，数值解的逼近效果会降低.从表 2可得出：随着插值离散点的增多，逼近的精度是先增，后趋于平缓或略有下降的趋势.对于等距节点，随着离散点的增多，插值结果会出现“龙格现象”，数值逼近结果会有轻微震荡和不稳定现象.而在相同插值点数下，Chebyshev点的逼近效果好于等距节点.因此，无论是点数还是逼近多项式的项数都需要选择合适，这也说明了影响重心有理插值逼近效果的因素与插值点的分布情况有关.最后，本文还用MATLAB画出了该方程的热流密度云图，图 3能很直观地看到在不同区域上热流的变化情况，箭头越长表示变化越快，黑色线条表示的是等温线，总趋势是由高温向低温区域扩散. 图 4表示的是重心有理插值在N=225时，选择Chebyshev节点离散，最终得到的数值相对误差图.

本算例考虑的是一个二维稳态的对流扩散方程，对流扩散也能客观描述热传递现象，常见传热方式有：导热、对流与辐射，物体的热量会从高温区传到低温区^[23].如果物体温度不随着时间的变化而变化，称为稳态，否则为瞬态导热.稳态传热的应用实例如保温墙和长热力管的管壁导热等.微粒在扩散时伴有流入和流出现象，促使扩散和对流两种物理特性互相耦合发生.求解的方程为

其中，(x，y)∈Ω=[0, 1]×[0, 1]，a(x，y)=2－x²－y，b(x，y)=e^x－y，方程(18)化简后的等价形式为

沿x方向的扩散项系数为A(x，y)=2－x²－y，y方向的扩散项系数为B(x，y)=e^x－y.

x方向的对流项系数为C(x，y)=－2x，y方向的对流项系数为D(x，y)=e^x－y.

源项函数：F(x，y)=－16x(1－x)(3－2y)e^x－y+32y(1－y)(32x²+y²－x－2).

精确解为u(x，y)=16xy(1－x)(1－y)，边界条件为u(x，y)=0，(x，y)∈Γ.

按照上述重心有理插值离散理论对算例3的方程与边界分别进行离散，离散点分别取等距节点和Chebyshev节点，区别在于求解的是二维稳态的对流扩散方程，并与Meshfree方法的数值解进行比较.使用重心有理插值配点法对方程(18)进行离散，对应的矩阵方程为

算例3采用置换法，对于矩形域来说，是将边界离散的方程替换掉原离散的M个方程组，再进行求解，其优点是统一处理边界，且得到的离散矩阵是方阵，一定程度上可以避免线性方程组系数的矩阵奇异化，也能提高代数方程的求解精度.矩阵方程(20)的等价方程可简写为

边界为Dirichlet边界，离散表达式为I _b u _b= F _b.其中F _b是零向量，其行数与左边微分矩阵u _b保持一致.在方程(21)中，D _x⁽²⁾和D _x⁽¹⁾分别表示x方向的二阶和一阶微分矩阵，D _y⁽²⁾和D _y⁽¹⁾分别表示y方向的二阶和一阶微分矩阵. I _m，I _n分别是单位矩阵，F _c是源项函数，常使用N×1的向量函数表示，记为F_N×1=f(x_i，y_j).同样经过控制方程与边界方程离散结果的组装，得到总的线性方程组A _L U = F，再求解出数值解U.最后，本文将重心有理插值配点法计算的数值结果与Kansa无网格配点方法进行了比较，该数值算例选自文献[24]第39章的第二个算例，无网格的基底函数分别选用了Gaussian函数和IMQ函数，离散点选择的是Halton点，用Kansa无网格配点法求解该方程时存在一个缺陷：当离散点较多时，离散矩阵的条件数比较大，容易引起数值解的不稳定性.具体的误差结果比较详见表 3和表 4.

通过表 3和表 4的比较能直观看出，重心插值配点法的逼近精度更高，如当N=25时Gaussian无网格法的逼近误差数量级为10^-2，而基于Chebyshev插值节点的重心有理插值配点法的数值误差数量级可达到10^-12.此外，重心插值配点法的条件数相对较小，数值解更加稳定，收敛速度接近指数收敛.对于Kansa无网格数值方法，其优点是离散点的选取相对自由，不受网格约束，缺陷是在处理高维问题或为了提高精度而加密插值点时，离散矩阵容易产生弱奇异现象.这些潜在问题容易引发数值解的不稳定性，需要结合正则化理论加以修正，实际上增大了计算时间.

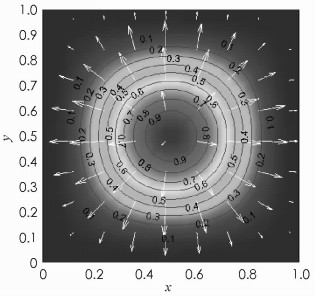
图 5是用重心插值配点法求解二维稳态对流扩散方程的数值解云图，云图的函数变化趋势相对平滑. 图 6是热流密度云图，从图 6可以看到梯度值的变化与流动方向.黑色线圈代表的是某时刻对应的等温线，可更直观地反映物质内部温度的分布情况.如果有多组瞬态图合成则可以制作成动态图，实时仿真物体在受热后温度是如何动态流动扩散的，也为瞬态对流扩散的研究奠定了基础.白色箭头越长表示温度变化趋势越快，该方面的研究也突显了数值解的直观与便捷的优势.

本文主要研究的是利用重心有理插值配点法求解一、二维变系数对流扩散方程，该数值方法是在重心Lagrange插值法的理论基础上改进权函数而得到的，改进后的插值性质更加稳定.本文总结了重心有理插值配点法常见的几种数值误差估计以及收敛性分析.全文总共包含了3个数值算例，计算结果表明：在相同网格尺寸下，Chebyshev点比等距节点的逼近效果要好.此外，重心有理插值配点法与古典隐格式、C-N格式、高精度紧致差分格式进行比较，可以看出重心有理插值配点法在数值精度与收敛阶上都有明显的优势.对于二维稳态的对流扩散问题，将重心有理插值配点法与非对称的Kansa无网格配点法进行比较，该方法的离散矩阵条件数更小，并且求解精度更高，再次验证了该方法的有效性.最后，本文还可视化热流密度云图，能更好地可视化数值结果，对于研究热扩散、对流强弱变化问题具有一定的应用价值.