-
随着计算机网络科技的迅猛发展,网络安全越来越受到人们的重视,入侵检测系统(intrusion detection system,IDS)作为当前网络安全领域内的热点问题受到研究人员的广泛关注[1]. 系统执行入侵检测时,IDS处理大量的数据,包括误报、不相关及冗余的特性. 这些特点不仅降低检测速度,而且消耗大量的计算资源. 特征选择通过对携带重要信息的相关特征进行识别,有助于解决IDS中遇到的常见问题[2-3].
由于特征选择是一个机器学习的概念,可以通过各种技术实现,包括智能模式、群体智能、人工神经网络、确定算法以及模糊和粗糙集[4]. 在入侵检测系统中,常常选择元启发式算法作为搜索最佳特征的方法. 目前,科研人员将多种群智能优化算法用于IDS的特征选择[5]. Acharya等[6]提出一种基于智能水滴算法的特征选择方法,通过智能水滴算法来选择入侵检测系统的特征,提高分类效果和检测率. Mohammadi等[7]提出一种基于特征选择和聚类的IDS过滤包装算法,利用线性相关系数技术和墨鱼算法对检测系统中的特征进行滤波、包装和分类. Selvakumar等[8]采用萤火虫算法对高维网络流量特征进行降维,降低误报率和计算时间. Alzubi等[9]为了提高入侵检测系统的性能,提出一种基于二值灰狼优化的入侵检测算法,该特征选择算法选取了最佳的特征数目,提高了IDS检测攻击的性能. 尽管上述方法能够在一定程度上完成基于特征选择的IDS检测,但是也存在检测准确率低和收敛速度慢等问题.
针对上述入侵检测系统中存在的问题,本文提出一种基于鸽群优化算法的入侵检测系统特征选择方法,该方法使用全局收敛最优的鸽群优化算法,通过考虑真阳性率(true positive rate,TPR)、假阳性率(false positive rate,FPR)和特征个数3个指标来选择特征的最佳子集. 为了加快算法的收敛速度,本文还采用一种基于余弦相似性的连续问题离散化方法,对元启发式算法进行二值化处理,使其更好地适用于离散问题.
HTML
-
鸽群优化算法(pigeon-inspired optimization,PIO)是胡春鹤等[10]根据鸽子回巢行为提出的一种新的群体智能优化算法,具有全局最优性和收敛速度快等优势. 鸽群优化算法通过模拟鸽群在不同阶段依据太阳高度、地磁场方向和地标等不同导航工具完成归巢的行为,来实现优化模型在解空间中的寻优过程. PIO算法大致分为磁场算子和地标算子2个阶段. 在磁场算子阶段,由于鸽群远离目的地,鸽群归巢行为采用太阳高度和地磁场作为导航工具;在地标算子阶段,由于鸽群离目的地较近时,可以观测到地表物体,因而采用地标作为归巢导航工具.
在D维搜索空间中,初始化鸽子种群数量为Np,在t次迭代中第i只鸽子的位置Xi(t)和速度Vi(t)可以表示为
在磁场算子阶段,所有鸽子在下一次迭代(t+1)时的位置Xi(t+1)和速度Vi(t+1)可以由下式更新为
式(3)中:R表示磁场因子,rand是[0, 1]范围内的均匀随机数,Xg表示当前迭代的全局最优解. 所有鸽子根据磁场因子来调整它们的飞行位置,并且其位置均由一个特定的目标函数来评估. 假定磁场算子阶段的最大迭代次数为nc1,如果当前迭代t > nc1时,中止磁场算子阶段,进入地标算子阶段.
在地标算子阶段,所有鸽子都是根据它们的适应值进行排序. 在每次迭代中,鸽子的数量由式(5)更新,其中只有一半的鸽子被考虑到计算中心鸽子的期望位置,而其他鸽子通过跟随期望的目标位置来调整它们的目的地. 理想目的地的位置由式(6)计算,而所有其他鸽子则通过式(7)更新位置.
式(5)中:Np(t)表示当前迭代t时的鸽子数量.
式(6)、式(7)中:Xc是中心鸽子的期望位置,Fitness(·)表示鸽群个体的适应度函数. 假定地标算子阶段的最大迭代次数为nc2,如果当前迭代t>nc2时,中止地标算子阶段. 通过每次迭代时最优位置的更新,获得全局最优解Xg.
-
本文采用一种基于鸽群优化算法的IDS特征选择算法,在PIO算法中采用两种不同的函数来定义鸽群个体的速度. 第一种是采用sigmoid函数(S函数)来离散鸽子的速度;第二种是对改进的二进制版本的基本PIO使用余弦相似度来定义鸽子的速度. 两种方式使用相同的适应度函数,但是每个版本都有不同的解决方案表达方式. 表 1显示了PIO到特征选择优化问题的映射过程.
-
适应度函数或目标函数是评价解的适应度的函数,适应度函数根据真阳性率(TPR)、假阳性率(FPR)和特征个数来评价作为所选特征子集的解. 特征数量包含在适应度函数中,如果存在任何特征但不影响TPR或FPR(解的质量),则倾向于消除它. 评估鸽群个体适应度表示为
式(8)中:SF和NF分别表示所选特征和总特征的数目,ωi(i=1,2,3)表示权重系数,本文权重值设置为ω1=0.1,ω2=ω3=0.45.
-
基于S函数的PIO特征选择通过一个长度等于特征数目的向量来定义鸽群数量,首先使用S函数将鸽子的速度转化为速度向量,然后使用式(10)将鸽子的位置二元化为位置向量,其中位置和速度向量的值最初是介于[0, 1]之间的随机数.
式(10)中:r表示一个均匀随机数.
使用传统方法通过式(3)计算每只鸽子的速度,然后使用一个S函数将速度转换为式(9)提出的二进制形式. 对于二值化的群智能算法,每只鸽子的位置将根据S函数值和(10)给出的在[0, 1]之间随机分布的概率进行更新. 除了在地标算子中更新位置,算法的其余部分将作为传统PIO的工作,进行最优位置的更新,获取全局最优解Xg.
-
第二种方式是利用余弦相似性计算鸽子的速度,由于该方式采用的是二值化,与基于S函数的PIO有3点不同之处:即鸽群个体的表示、新位置和速度的计算、允许鸽群在特定条件下加入新的个体,从而增加了达到最优解的机率.
-
基于余弦相似度的PIO方法中的解是一个具有特征数目长度的向量,解的值由随机二进制值0或1初始化. 值0表示当前解中没有对应的特征,值1表示解中存在对应的特征.
-
磁场因子是根据群中最佳鸽子的速度和位置更新鸽子位置的主要参数. PIO的工作原理是从式(3)所述的鸽群中全局最优位置减去当前鸽子的位置Xi. 但是,在二进制PIO中,需要采用新的方程模拟上述过程,更新鸽的位置Xp和速度,使之向全局最优位置Xg的方向移动. 鸽子速度的计算取决于解之间的相似度,所以每个鸽子都有不同的速度值. 速度的计算基于余弦相似度公式,通过求解局部解Xp与整体解Xg之间的相似比获得. 二进制PIO中的鸽子速度和位置更新由式(11)、式(12)给出
根据式(12),如果解不是全局解邻居,则向全局解更新其位置的概率高于当前解是全局解邻居的概率.
-
地标因子第一部分是计算鸽子的目的地,该部分与基本PIO算法的计算相同. 所有鸽子根据各自的适应度值来排列,在每次迭代中鸽子的数量由式(5)更新,其中只有一半的鸽子被认为是计算中心鸽子的期望位置,其他鸽子通过跟随期望目的地位置来调整它们的目的地. 期望目的地的位置由式(6)计算.
地标因子第二部分,所有鸽子都向所需目的地更新它们的位置,由于所需目的地是一个二进制向量,因此所有鸽子都会通过式(11)计算各自的速度,然后利用式(12)更新位置.
-
另一个二元PIO特征选择的改进之处是在鸽群中引入新的个体. 这个过程的灵感来源于二进制PIO中很可能存在重复的解或鸽子,新个体的加入在磁场算子阶段完成.
2.1. 适应度函数
2.2. 基于S函数的PIO特征选择
2.3. 基于余弦相似度的PIO特征选择
2.3.1. 鸽群个体的表示
2.3.2. 改进的磁场因子
2.3.3. 改进的地标因子
2.3.4. 引入新鸽子
-
为了验证算法的有效性,本文使用KDDCUP 99[11]和UNSW-NB15[12]两个数据集评估基于PIO的特征选择算法,并且将测试结果与基于分类器(SVM)的特征选择技术[1],基于二进制灰狼优化算法(BGWO)的特征选择技术[9],基于递归特征消除和随机森林(RFE-RF)混合的特征选择技术[12],基于贪婪和遗传算法(GS-GA)混合的特征选择技术[13],基于粒子群优化、蚁群算法和遗传算法(PSO-ACO-GA)混合的特征选择技术[14]等其他网络入侵检测系统特征选择算法进行了比较. 所有特征选择算法都使用python语言Scikit学习库的决策树(decision tree,DT)分类器进行评估,使用原因是DT与其他基本分类器相比可以轻松处理特征交互. 测试中使用的个体种群数量为20,迭代次数为100,磁场因子设置为0.3.
-
本文采用KDDCUP 99和UNSW-NB15两个当前流行的数据集对所提出的特征选择算法进行评估.
KDDCUP 99数据集是1999年基于DARPA数据集的一个改进版本,用于开发入侵检测系统,目的是区分坏连接和好连接. 该数据集主要用于模拟4种不同类型的攻击:拒绝服务攻击(DoS)、用户到根攻击(U2R)、远程到本地攻击(R2L)和探测攻击. KDDCUP 99数据集在训练和测试集中分别包含4 898 431和311 029个连接,训练数据集包含24种攻击,而测试集包含14种不存在于训练集中的新类型攻击. KDDCUP 99有41个特征,可以分为3大类:基本特征、流量特征和内容特征.
UNSW-NB15数据集是由IXIA的PerfectStorm平台开发的,用于模拟和生成真实的攻击模型. 它是一个名为Tcpdump的工具,包含多达100 GB的Pcap文件,用于模拟9种不同类型的攻击. 这些攻击包括DOS、外壳代码、蠕虫、模糊器、后门、攻击、分析、通用和侦察. 该数据集具有49种特征,如时间特征、内容特征等.
-
评价特征选择算法的度量值有许多种,本文使用真阳性率TPR、假阳性率FPR、准确率Accuracy和F-分数4个性能指标来评估IDS. 这4个评估指标可以使用基于表 2表示.
根据评估指标定义公式如下:
真阳性率是测量正确识别实际攻击的比例
假阳性率是测量识别为攻击的正常部分比例
准确率是衡量正确分类类别占分类总数的比例
F-分数通过同时考虑精确率和召回率来衡量模型的准确性
-
本文通过TPR、FPR、F-分数和准确率等指标对所研究的算法进行评价,所有的测试结果为运行30次后的平均值. DT通过使用指定特征训练模型来评估用于特征选择的每个算法,然后使用测试集评估模型. 为了保证比较的公平性,所有的模型都在同一数据集上训练,训练方法相同. 表 3给出了不同特征选择算法在KDDCUP 99数据集选定的特征数量及相应的组信息.
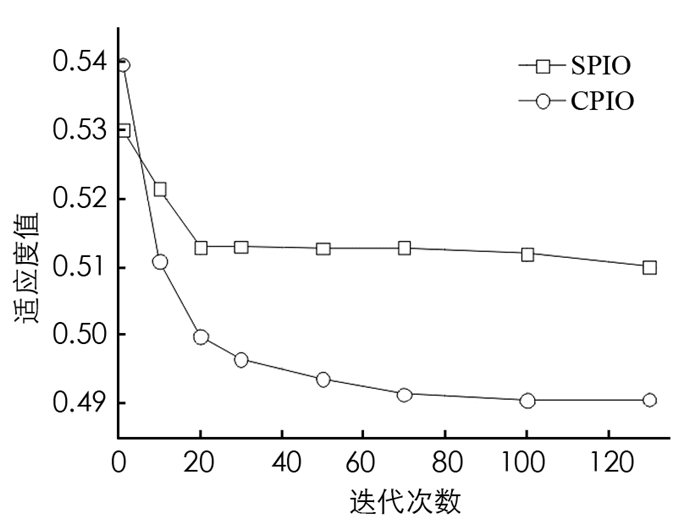
图 1给出了基于Sigmoid函数(SPIO)和余弦相似度(CPIO)的PIO二值化收敛曲线. 本文算法的目标是最小化解的适应度值,测试结果表明基于余弦相似性对解的速度进行二值化的方法比基于Sigmoid函数二值化的方法具有更快的收敛速度. 从图 1中可以看出,在前30次迭代中,CPIO以指数衰减收敛,一直增强解的质量;而SPIO的收敛速度比CPIO慢,并且在第60次迭代时解质量停止了增强,从而证明本文提出的余弦相似法用于离散PIO比传统的离散化连续算法收敛快得多. CPIO引入新鸽群个体加入算法有助于算法保持解的增强,同时容易避免算法陷入局部最优解.
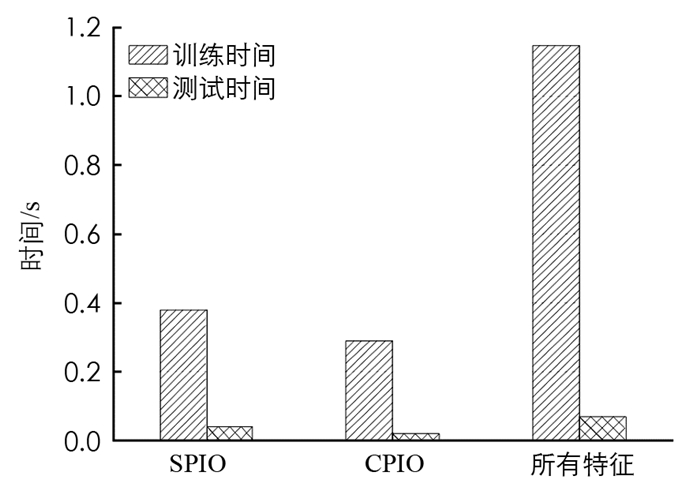
影响特征选择算法解决方案质量的另一个度量是所选特征的数量. 特征数量影响模型构建和测试时间. 图 2给出了3种情况下的训练和测试时间,所采用的数据集为KDDCUP 99:①使用数据集中的所有特征(41个特征);②使用SPIO选择的10个特征;③使用CPIO选择的7个特征. 从图 2中可以看出,特征数目影响了模型的建立和测试所需的时间.
表 4给出了不同特征选择算法在KDDCUP 99数据集上进行测试的TPR、FPR、F-分数和准确率对比结果. 从表 4中可以看出,本文所提出的CPIO方法比其他网络入侵检测系统特征选择算法获得最高的TPR、F-score和准确率,同时最低的误报率(FPR),从而说明本文所提方法的性能更优. 而且,本文所提出的SPIO方法与基于二进制灰狼优化算法的特征选择方法取得了几乎相同的效果,但是使用SPIO进行特征训练的模型比基于二进制灰狼优化的训练模型更稳定.
表 5给出了不同特征选择算法从UNSW-NB15数据集中选择的特征信息. 表 6给出了在UNSW-NB15上训练和测试DT分类器的30次运行的平均值. 表 6中的结果表明,与其他算法相比,本文提出的CPIO方法具有良好的性能,能够在保证高检测率、低误报率的前提下,减少构建鲁棒IDS所需的特征数目.
3.1. 数据集
3.2. 评估指标
3.3. 实验结果
-
本文提出了一种基于改进鸽群优化算法的入侵检测系统特征选择方法,用于解决当前入侵检测系统中存在的检测准确率低、建模时间长以及收敛速度慢等问题. 该方法采用鸽群优化算法对数据中的不相关特征进行优化,在保证高检测率、低误报率的前提下,通过减少构建鲁棒IDS所需的特征数目来降低模型建立所需的训练时间. 在对连续群智能算法进行离散化处理时,通过引入基于余弦相似性的二值化技术,提高了算法的收敛速度. 实验结果表明,与其他算法相比本文方法对真阳性率、假阳性率、F-分数和准确率等指标的测试效果更佳,能够有效处理IDS的检测问题.






 DownLoad:
DownLoad: