Notes on Density of Geodesics on Surface of Constant Curvature

几何是数学中最为直观、具体且与现实生活最为贴近的一门数学分支^[1-2]，非欧几何是欧氏几何的进一步推广，常曲率曲面是欧氏平面的推广，常曲率曲面上测地线集的密度是积分几何中重要的概念. 文献[3]运用常曲率曲面上测地线集的密度将平面上经典的Cauchy-Crofton公式推广到了常曲率曲面上. 关于平面上直线集的密度可参见文献[4-5]. 文献[6-8]研究了常曲率曲面上测地线集的密度. 受文献[7]的启发，本文利用常曲率曲面上基本的三角公式证明了常曲率曲面上的测地线集的密度与坐标选取无关，还得到了常曲率曲面上测地线集密度的其他形式.

曲面的Weingarten变换是曲面切平面到自身的一个自共轭变换. Weingarten变换在P∈S点的两个实特征值称为曲面S在P点的主曲率，分别记为k₁，k₂，K=k₁k₂称为曲面的Gauss曲率. Gauss曲率K为常数的曲面称为常曲率曲面.

记高斯曲率恒为常数ε的曲面为Σ_ε，不失一般性，本文仅考虑ε取1，0，-1的情形. 即ε=1时，Σ₁为单位球面；ε=0时，Σ₀为欧氏平面；ε=-1时，Σ_-1为双曲平面.

Σ_ε上测地曲率恒等于0的曲线称为测地线，欧氏平面上的测地线为直线，单位球面上的测地线为大圆. 在曲面Σ_ε上选一条测地线作为v-曲线：u=0. 取与v-曲线正交的测地线族作为u-曲线：v为常数. 再取u-曲线的正交轨线作为v-曲线. 在这样的半测地线坐标网下，曲面Σ_ε的第一基本形式简化为^[9-11]

定义函数

关于以上函数，有^[2]

Σ_ε上以a，b，c为边，α，β，γ为对应角的测地三角形满足以下公式^{[3, 12]}：

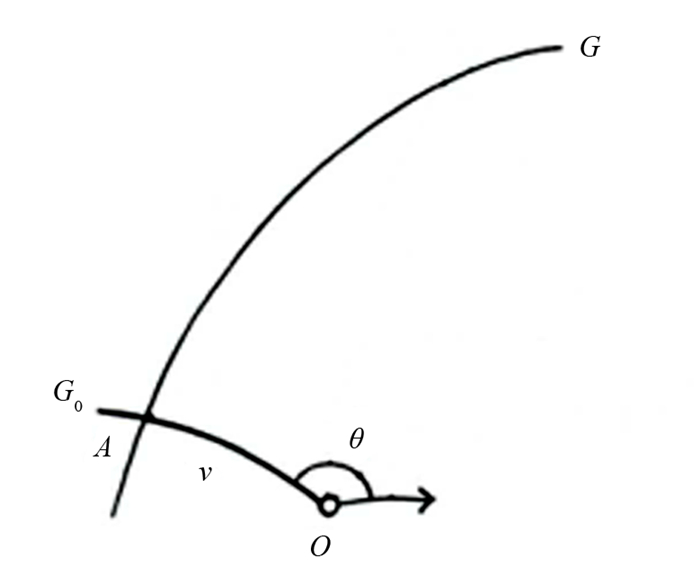
取定Σ_ε上的一点O，以及O处的一个方向. G为Σ_ε上的一条测地线. 已知有唯一一条测地线G₀过O点，且与G正交于点A，记v为O沿G₀到G的距离，即$\hat{O A}=v, \theta $为G₀与O处取定的方向所形成的夹角(图 1). 则测地线集{G}的密度定义为

Σ_ε上测地线集的密度$\mathrm{d} G=c n_{\varepsilon}(v) \mathrm{d} v \wedge \mathrm{d} \theta $是在欧氏空间运动群下的不变密度^{[8, 13]}.

定理1    常曲率曲面Σ_ε上测地线集的密度与固定点O以及点O处的固定方向的选取无关.

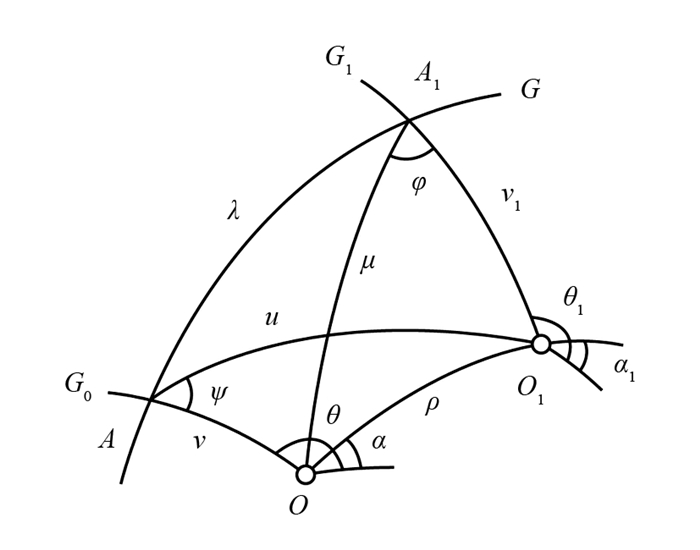
证   现考虑Σ_ε上另一固定点O₁，以及O₁处的一个固定方向. 可知过O₁有唯一一条测地线G₁与G正交. 记G₁与G相交于A₁，且G₁与O₁处的固定方向所形成的夹角为θ₁. 并将OA，OO₁，OA₁用测地线段连接起来. 记α，α₁为测地线OO₁分别与O，O₁处的固定方向所形成的夹角(图 2). 为了方便，我们还记

在测地三角形ΔOO₁A₁中应用(3)式，有

在测地三角形ΔOAA₁中应用(2)式，有

将(7)式代入到(6)式，得

类似地，在测地三角形ΔOO₁A和测地三角形ΔO₁AA₁中先后应用(3)式与(2)式，有

由(8)式和(9)式可知

在测地三角形ΔOAA₁中用(3)式，可得

在测地三角形ΔOO₁A₁中用(2)式，可得

由(11)，(12)式可知

类似地，在测地三角形ΔO₁AA₁和ΔOO₁A中应用(3)式和(2)式，有

则由(13)，(14)式，可将(10)式化简得

即

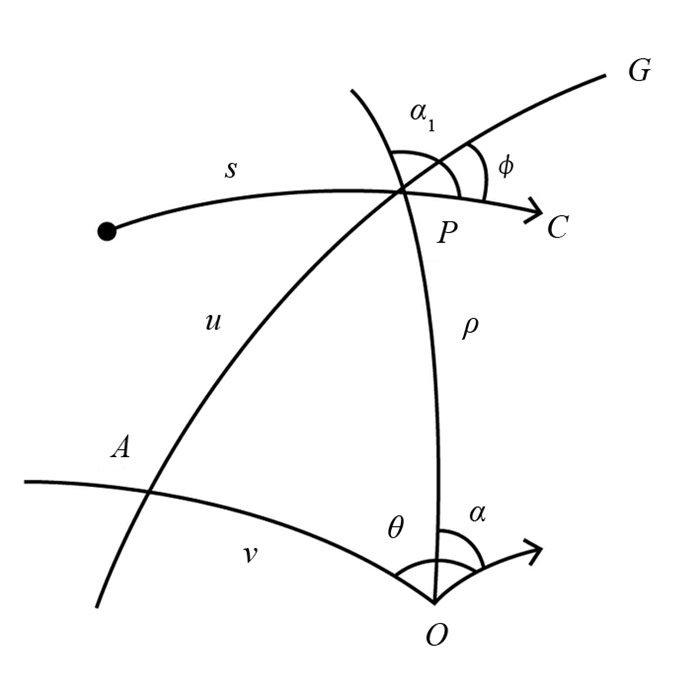
综上所述，测地线集的密度$\mathrm{d} G=c n_{\varepsilon}(v) \mathrm{d} v \wedge \mathrm{d} \theta $并不取决于固定点O以及点O处所选择的固定方向.

定理2    若测地线G与常曲率曲面Σ_ε上一曲线C相交，取其交点之一P，并且在P点，C与G所形成的夹角为ϕ，s为曲线C上P处的弧长参数(对于C上某一初始点). 则测地线集{G}的密度为

证    设G与常曲率曲面Σ_ε上一曲线C相交(图 3).

取v为常数的曲线是和测地线OA正交的测地线，u为常数的曲线是它们正交的轨迹. 曲线C在此半测地坐标网下有

因此，如果测地线G(v为常数)与曲线C相交于点P，并形成夹角ϕ，则

从而

因此(5)式可写作

记ρ为测地线段OP的弧长，u为测地线段AP的弧长，α为测地线OP与O点处固定方向所形成的夹角，α₁为测地线OP与C所形成的夹角. 在测地三角形ΔOAP中，由(3)，(2)式，有

微分可得

又在测地三角形ΔOAP中，由(1)-(3)式可推得

因此

代入到(23)，(21)式后可得

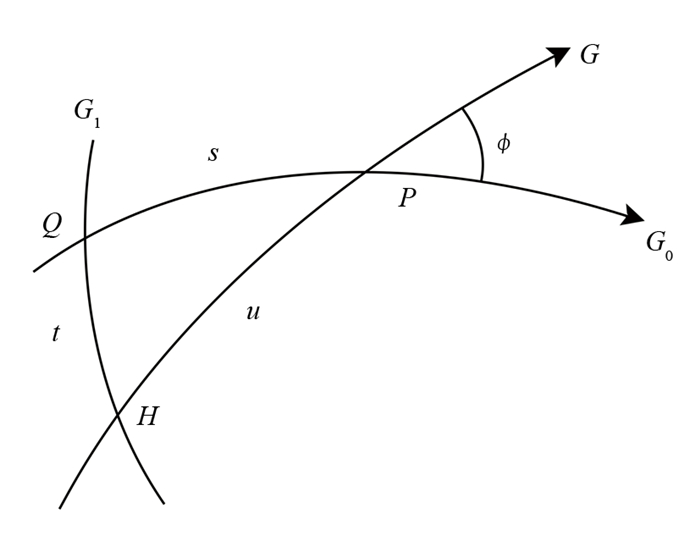
定理3    若测地线G与常曲率曲面Σ_ε(ε≠0)上两相互正交于Q点的测地线G₀，G₁分别相交于P，H，记$\hat{Q P}=s, \hat{Q H}=t $. 则测地线集{G}的密度公式为

证   在测地线G上$ \hat{H P}=u$，点P处G₀与G的夹角为(图 4).

在测地三角形ΔQHP中运用(1)式，可得

微分可得

代入定理2中得到的测地线密度公式，可得

在测地三角形ΔQHP中运用三角公式

可得

代入(29)式，有