A Method for Solving Conflict Problem of Ecological Slope Protection Based on Extension Knowledge Mining

可拓学是我国学者蔡文1983年创立的一门原创性横断学科^[6]. 它以形式化的模型, 探讨事物拓展的可能性以及开拓创新的规律与方法, 并用于解决现实中的矛盾问题, 以摆脱求解矛盾问题时对经验、灵感等个体能力的过度依赖^[7-9]. 可拓学的逻辑细胞是基元, 包括物元M、事元A及关系元R^[9]. 基元形式化地表达为B=(O, C, V), 其中, O为对象, C为特征, V为关于特征所取的量值, 量值可以是定量的数字, 也可以是定性的描述. 可拓知识包括发散型知识、相关型知识、蕴含型知识、可扩型知识和共轭型知识等.

1) 发散分析原理

① 由一个基元出发, 可以拓展出多个同对象基元, 且同对象基元集一定是非空的, 即B=(O, c, v)-|{(O, c₁, v₁), (O, c₂, v₂), …, (O, c_n, v_n)}={(O, c_i, v_i), i=1, 2, …, n}. 根据该原理, 如果某一基元不能解决矛盾问题, 可以考虑利用该基元的对象与其他特征组成的新基元去解决.

② 由一个基元出发, 可以拓展出多个同征基元, 且同征基元集一定是非空的, 即B=(O, c, v)-|{(O₁, c, v₁), (O₂, c, v₂), …, (O_n, c, v_n)}. 根据该原理, 如果一个基元不能解决矛盾问题, 可以考虑利用与它同特征的其他对象构成的新基元去解决.

2) 相关分析原理

给定物元M(t)=(O_m(t), c_m, c_m(O_m(t))), 则至少存在一个同征物元M_c(t)=(O′_m(t), c_m, c_m(O′_m(t)))或同物物元M_O(t)=(O_m(t), c′_m, c′_m(O_m(t)))或异物物元M′(t)=(O′_m(t), c′_m, c′_m(O′_m(t))), 使M(t)~M_c(t), 或M(t)~M_O(t), 或M(t)~M′(t). 符号“~”表示相关. 根据该原理, 用某一物元不能解决矛盾问题时, 可以考虑利用与其相关的物元去解决.

3) 蕴含分析原理

若B₁实现必有B₂实现, 记作B₁@必有B₂@, 或B₁⇒B₂, 称B₁蕴含B₂；若B₁与B₂同时实现必有B实现, 则称B₁, B₂与蕴含B, 记作B₁∧B₂⇒B；若B₁或B₂实现都有B实现, 则称B₁, B₂或蕴含B, 记作B₁∨B₂⇒B；若B₁⇒B₂, B₂⇒B₃, 则B₁⇒B₃, 也可记作B₁⇒B₂⇒B₃. 符号“⇒”左边是下位基元, 右边是上位基元. 根据上述原理, 当上位目标不容易实现时, 可以考虑寻找其下位目标, 如果下位目标容易实现, 则认为找到了解决矛盾问题的方法.

4) 可扩分析原理

可组合性：给定基元B₁=(O₁, c₁, v₁), 则至少存在一个基元B₂=(O₂, c₂, v₂), 使B₁和B₂可以组合成B. 此时, B=B₁+B₂(聚合, 即B₁与B₂可加), 或B=B₁⊗B₂(构成系统, 即B₁与B₂可积)；可分解性：任何基元可以按一定的条件分解为若干基元；可扩缩性：设B=(O, c, c(O)), 则在条件l下, 必存在实数α(α＞0), 使αB=(αO, c, αv), 当0＜α＜1时, 称基元B可缩小为αB, 当α＞1时, 称基元B可扩大为αB. 根据以上原理, 当一个基元不能解决问题时, 可以考虑应用其分解、扩大、缩小后形成的基元, 与其他基元组合成的新基元来解决矛盾问题.

5) 共轭分析原理

任何事物都具有共轭部, 即：实部、虚部、虚实中介部；或软部、硬部、软硬中介部；或潜部、显部、潜显中介部；或关于特征c的负部、正部、负正中介部. 每对共轭部和它们的中介部之和等于原物, 且任何物的一对共轭部中, 某一共轭部至少有一个特征与其对应的共轭部中的某个特征是相关的. 根据以上原理, 当物的某一部不能解决矛盾问题时, 可以考虑应用其对应的共轭部来解决.

某高速公路土质路堤, 设计一级边坡高8 m, 坡率为1∶0.75；二级边坡高6 m, 几乎不具备放坡条件, 现拟对该处路堤进行综合防护, 既保证路堤边坡稳定, 又要确保边坡具有较高的植被覆盖率.

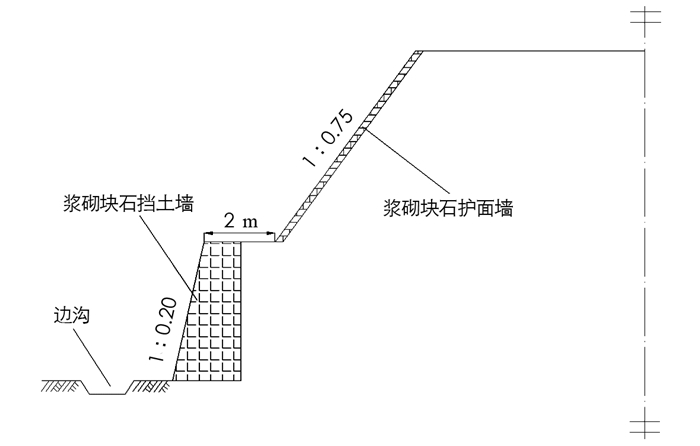
经计算, 若不进行任何防护, 该路堤的稳定性不满足规范要求, 而直接在路堤坡面实施复绿难以快速稳定边坡. 为确保边坡稳定, 一级边坡用浆砌块石护面墙防护, 二级边坡用浆砌块石挡土墙加固, 圬工防护完成后如图 1所示, 由于路堤稳定性验算以及圬工防护部分不是本文讨论的重点, 这里不展开赘述.

该路堤边坡下部采用挡土墙加固, 上部用的传统形式浆砌块石护面墙防护来稳定边坡, 挡土墙可以直接提高边坡稳定安全系数, 而上部的浆砌块石护面墙具有封闭边坡表面、防止雨水冲刷的防护作用, 进而能维持边坡的稳定性. 但是, 使用这些防护措施以后, 坡面已不具备生态防护所需要的种植层, 目标与条件之间存在冲突. 根据前述的可拓学原理, 基元中的对象、特征、关于特征的量值等, 都可以不断地拓展、发散, 形成多个新的基元(即可以挖掘的可拓知识), 这样, 就有可能用这些新的基元来解决这个冲突问题.

该问题的目标是使边坡具有较高的植被覆盖率. 设目标基元G=(边坡, 坡面植被覆盖率, 较高), 条件基元为L, L={l₁, l₂, l₃, l₄, l₅, …}(这里仅列出一些主要条件), 其中l₁=(坡面, 种植层, 无), l₂=(路堤, 防护措施, 下部挡墙∧上部护面墙), l₃=(护面墙, 坡率, 1∶0.75), l₄=(挡墙墙面, 坡率, 1∶0.20), l₅=(护坡道, 宽度, 2 m), 则该冲突问题的可拓学模型为P=G*L, G↑L, 在现有条件L下, 目标G难以实现, 故该冲突问题P是可拓学中的不相容问题.

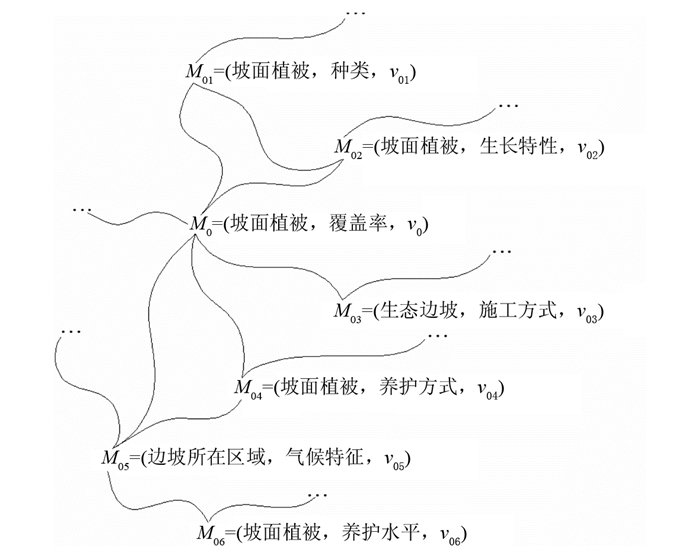
设物元M₀=(坡面植被, 覆盖率, v₀), 参照笔者以前的研究^[10], 以M₀为出发点, 用相关分析原理挖掘其相关型知识, 可建立M₀的网如图 2所示.

对M₀的相关网中的一些物元, 再进行发散分析. 例如对M₀₁中关于坡面植被的特征“种类”的量值进行发散分析, 可得到用发散树形式表示的发散型知识：

至此, 目标G仍无法实现, 因为坡面不具备种植层. 继续对M₀₂, M₀₃中关于特征的量值进行发散分析, 得发散型知识：

由于坡面不具备种植层, 故由M₀₂发散出的物元也不能实现目标G. 结合由M₀₃发散出的物元进行分析, 实际上现在的客土喷播技术可以实现目标G. 为得到更多的生态护坡设计方案, 对施工方式进一步进行发散分析, 得发散型知识.

综合考虑由M₀₁, M₀₂, M₀₃, M₀₃₁发散出的物元, 结合该边坡实际情况, 本专业领域的技术人员应该可以得到以下启示：坡脚(挡土墙下部)边沟两侧具备所需的种植层, 将M₀₃₁, M₀₃₁₃, M₀₁₂, M₀₂₂结合在一起可使目标G实现, 也就是在坡脚边沟两侧的植层上就地种植具有垂吊生长特性的藤本植物, 植物向上生长后可覆盖坡面. 选择哪种藤本植物应结合物元M₀₄, M₀₅, M₀₆以及现有条件l₃, l₄等确定, 用该方法实现目标G的关键是利用了物元(种植层, 位置, v₁)=M₁, 其中, v₁=坡脚边沟两侧, 而目标要求却是实现边坡较高边的植被覆盖率, 即本法的实质是利用目标所指地点之外的条件来实现目标, 消解冲突, 使G↓L.

进一步地, 如果要尽快使边坡实现植被覆盖, 容易想到采取多处同时种植的方式, 为解决边坡其他部位无种植层的问题, 可以对物元M₁继续进行发散分析, 得发散型知识：

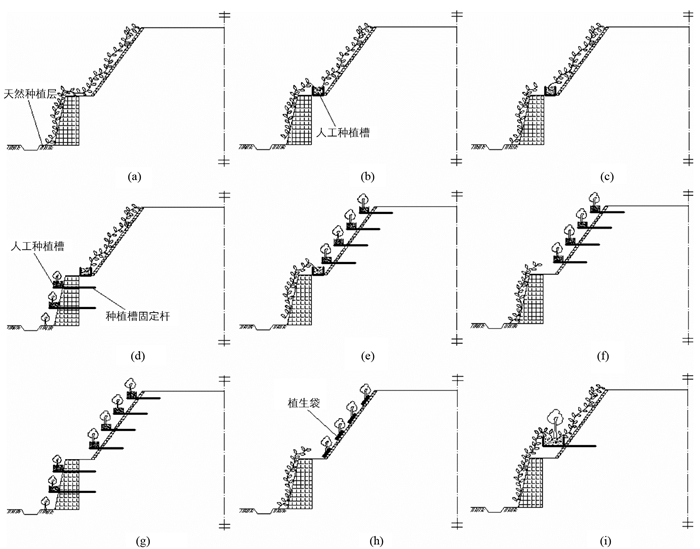
综合考虑由M₁发散出的物元, 可以得到以下启示：将公路土质路基开挖路段可用的弃土, 或(和)公路沿线软基开挖的可用弃土, 或(和)公路范围以外的种植土移运过来, 放在边坡的适当位置, 就可以用作生态护坡的种植层, 实现就地种植, 从而使目标G实现. 移运来的种植土, 可放在坡脚, 或(和)坡面, 或(和)坡顶, 则有物元(种植层, 位置, 坡脚∧(∨)坡面∧(∨)坡顶)=M₂. 由此可得蕴含型知识：M₂⇒M₀₃₁⇒M₀⇒G, 也就是将种植层的位置选在坡脚和(或)坡面和(或)坡顶, 可实现就地种植, 从而实现所需的植被覆盖率, 消解冲突, 使G↓L. 这样就可得到生态护坡的多种方案(图 3)：通过在坡脚的种植层上种植攀援植物, 或(和)在人工种植槽中种植攀援或垂吊植物, 实现边坡的生态防护. 这些方案中, 攀援植物防护^[11-12]、在挡墙上放置种植槽^[13]、植生袋护坡等技术^[14-15]已经在工程中得到了应用. 此时, 坡脚处和(或)坡面上以及坡顶处都有了种植层, 坡面植被实际上已经不限于藤本植物了. 将公路土质路基开挖路段的弃土, 或(和)公路沿线软基开挖的弃土用作种植层, 也体现了共轭型知识的运用, 弃土对于路基施工面言是负部物元(无用的), 而对于边坡种植层而言却是正部物元(有用的). 图 3中(d), (e), (f), (g), (i)等使用的人工种植槽, 还体现了可扩型知识中的可组合型知识的运用, 即：人工种植槽=种植槽⊕固定杆, 这样种植槽便可固定于坡面.

图 3中的方案各具特点, 选择哪种方案应根据工程实际情况, 通过技术经济分析确定. 总体上看, (a)方案施工成本较低, 但植被覆盖大部分坡面所需时间较长；(b), (c), (i)方案需安装人工种植槽, 但复绿较快；(d), (e), (f), (g)方案需要安装多个人工种植槽, 但复绿速度更快, 且容易结合边坡绿化营造艺术景观；(h)方案为植生袋护坡加常规种植的方案, 技术成熟, 复绿也较快.

从以上实例分析可以得知, 以边坡防护的目标基元为出发点, 依据可拓分析原理, 挖掘目标基元的可拓知识, 就可以沿着不同的途径拓展出多个基元, 从而获得更多的有效信息, 为分析和解决矛盾提供大量资料. 在挖掘可拓知识的过程中, 重点在于求量, 应该拓宽思路, 拓展出尽可能多的新基元, 以克服常规设计中的思维定势. 在此基础上, 根据现有客观条件和解决问题的需要, 从可行性、优劣性及相容性等出发, 对拓展得到的大量基元进行评价, 筛选出符合条件的少量基元, 即进行收敛分析, 收敛分析的要点是求质. 解决矛盾问题的方法不应该是单一的, 可以确定, 如果对物元M₀相关网中的相关关系进行变化^[16], 或者继续扩大对物元M₀的相关分析, 并不断对其拓展出的相关基元中的对象、特征、关于特征的量值等进行发散分析, 还将得到更多的生态护坡创意方案.

在坡面不具备种植层时, 运用可拓知识挖掘方法获取边坡生态防护创意方案的一般流程如下：

1) 明确生态护坡的目标, 并将其以基元的形式表达出来.

2) 挖掘目标基元的相关型知识, 以相关网的形式表达这种知识.

3) 挖掘相关网中的基元的发散型知识, 以发散树的形式表达这种知识.

4) 从上述发散型知识中, 结合专业知识, 寻找能解决问题的基元或基元的组合, 从而形成能使目标实现的蕴含型知识, 最终形成生态护坡的潜在方案.

通过实施上述分析, 通常可以得到多个生态护坡潜在方案, 第4步完成后应对各方案进行技术经济比较, 选择较优方案. 笔者用该流程分析过许多生态护坡实例, 多数情况可用该流程解决问题, 得到较好的防护方案, 若遇到不能得到较好方案时, 可参考以下思路：

在第2步中, 继续挖掘目标基元的相关型知识, 即将目标基元的相关网扩大, 确保不漏掉对实现生态护坡目标有影响的主要因素；在第3步中, 除挖掘基元的发散型知识外, 再挖掘基元的蕴含型知识和可扩型知识, 如果目标基元是以物元的形式表示的, 还可以挖掘其共轭型知识, 在第3步中, 应特别重视对坡面植被种类、生态护坡施工方式的发散分析.

针对坡面不具备种植层这一条件与生态护坡目标相冲突的矛盾问题, 本文提出了一种基于可拓知识挖掘的冲突消解方法. 运用可拓知识挖掘的方法解决矛盾问题、化解冲突, 其核心思想是“拓展”, 通过对基元中的对象、特征、关于特征的量值等不断进行拓展分析, 形成有助于解决问题的新知识, 从而能够结合专业知识, 形成解决问题的方案. 事实上, 边坡防护中很多新技术的发明过程, 也是有意或无意地运用了可拓知识的过程, 运用可拓知识进行边坡生态防护设计, 最大的优势在于可以摆脱设计过程中对个体能力、经验、灵感等的过度依赖. 从本文的案例分析可以看出, 在新理念公路设计的背景下, 将可拓知识运用于边坡的生态防护设计中是可行的, 具有重要的工程应用价值.