-
本文考虑下面的无约束优化问题:
这里f:
${\mathbb{R}^n} \to \mathbb{R}$ 是一个光滑函数,$\mathbb{R}^n$ 表示n维欧氏空间,函数f的梯度记为g(x):=▽f(x). 在实际求解大规模无约束优化问题中,建立一些具有低存储的快速数值算法是十分重要的. 共轭梯度法是求解大型无约束优化问题(1)的一类十分有效的方法[1],其通常的迭代形式如下这里xk∈
$\mathbb{R}^n$ 是一个解的第k次逼近,αk > 0是由一种合适的线搜索所确定的步长,dk∈$\mathbb{R}^n$ 是搜索方向,其定义如下其中:gk表示梯度g(xk),βk∈
$\mathbb{R}$ 为共轭参数. 步长αk由标准的Wolfe线搜索或者强Wolfe线搜索
确定,其中0 < δ < σ < 1. 不同的共轭梯度法对应不同的共轭参数βk. 众所周知的共轭梯度法包括Hestenes-Stiefel(HS)[2],Polak-Ribière-Polyak(PRP)[3-4],Dai-Yuan(DY)[5],Liu-Storey(LS)[6],Fletcher-Reeves(FR)[7]和Conjugate-Descent(CD)[8],它们所对应的共轭参数如下
其中yk-1:=gk-gk-1且||·||表示欧氏范数. 目标函数是一个严格凸二次函数并且步长由精确线搜索得到,且在一般情形下,它们的理论性质和数值表现不尽相同. 众所周知,DY法、CD法和FR法具有良好的收敛性质,但它们的数值计算效果一般;相反,PRP法、HS法和LS法具备出色的数值表现,但它们可能不收敛. 为了获得收敛性数值效果的算法,不少学者对共轭参数自身作了一些改进[9-10]和一些混合[11-12]. 本文主要考虑共轭梯度法的混合形式. 文献[13]通过对PRP法和DY法进行凸组合,得到一种新的共轭梯度法,其共轭参数如下
其中参数θk∈[0, 1]由共轭条件
$\boldsymbol{y}_{k-1}^{\mathrm{T}} \boldsymbol{d}_{k}=0$ 确定. 最近,文献[14]对PRP法和FR法进行凸组合,引进了一种混合共轭梯度法:这里参数θk∈[0, 1]根据求解优化问题
$\mathop {\min }\limits_{_{{\theta _k}}}\left\{\left\|\boldsymbol{d}_{k}^{H C G}-\boldsymbol{d}_{k}^{Z Z L}\right\|^{2}: k \geqslant 1\right\}$ 得到. 在标准的Wolfe线搜索条件下,该算法具有全局收敛性和良好的计算表现.受文献[14]的启发,本文构造了一种新的混合共轭梯度法
这里
其中
为优化问题
$\mathop {\min }\limits_{_{{\theta _k}}}\left\{\left\|\boldsymbol{d}_{k}^{\mathrm{NH}+}-\boldsymbol{d}_{k}^{\mathrm{NYF}}\right\|^{2}: k \geqslant 1\right\}$ 的最优解. 基于共轭参数βkNH+所得相应的共轭梯度法称作NH+算法或NH+法. 因为文献[15]提出的ZZL法是文献[16]提出的NYF法特殊情况. 因此,文献[14]提出的方法是NH+法的特殊情况(当pk=gk即为文献[14]中的方法).
HTML
-
基于共轭参数βkNH+的计算公式(5),所得的NH+算法如下:
NH+算法
步骤1:给定初始点x1和精度ε. 置k=1,令d1=-g1.
步骤2:若||gk||≤ε,终止. 否则,转步骤3.
步骤3:通过(3)式计算搜索方向dk.
步骤4:由标准的Wolfe线搜索(4)确定步长因子αk.
步骤5:由(2)式计算下一个迭代点xk+1.
步骤6:令k:=k+1,转步骤2.
-
为了论证算法NH+的收敛性,给出了如下的基本假设.
假设1 水平集S={x:f(x)≤f(x0)}有界,即存在
$\tilde a$ > 0,对于任意x∈S,有‖x‖≤$\tilde a$ .目标函数的梯度函数在S的某邻域U内Lipschitz连续,即存在常数L > 0,对任意x,y∈U,有‖g(x)-g(y)‖≤L‖x-y‖.
由假设可知存在常数γ > 0,对任意x∈S,有
以Zoutendijk条件为基础给出如下引理1. 这个引理在论证共轭梯度算法的全局收敛性过程中具有重要的作用.
引理1 假设1成立,算法NH+的搜索方向是下降的,步长满足标准Wolfe线搜索条件,则Zoutendijk条件即
$\sum_{k=0}^{\infty} \frac{\left(\boldsymbol{g}_{k}^{\mathrm{T}} \boldsymbol{d}_{k}\right)^{2}}{\left\|\boldsymbol{d}_{k}\right\|^{2}}<\infty$ 成立.证 由标准Wolfe线搜索条件(4),知
另一方面,由假设1和(2)式,有
再结合算法NH+的下降性,得
进一步由(4)式知
对(7)式从k=1,2,…,∞求和,并注意目标函数f(x)有下界,即知Zoutendijk条件成立. 因此,结论得证.
下面的引理是论证算法NH+全局收敛性的关键. 这个引理的具体论证过程可参见文献[17].
引理2[17] 假设1、充分下降性、标准Wolfe线搜索条件均成立. 若
$\sum_{k=0}^{\infty} \frac{1}{\left\|\boldsymbol{d}_{k}\right\|^{2}}=\infty$ ,则$\mathop {\lim \inf }\limits_{k \to \infty } \left\|\mathit{\boldsymbol{g}}_{k}\right\|=0$ .注 通常利用的是引理2的逆否命题,即若
$\mathop {\lim \inf }\limits_{k \to \infty }\left\|\mathit{\boldsymbol{g}}_{k}\right\| \neq 0$ ,则$\sum_{k=0}^{\infty} \frac{1}{\left\|\boldsymbol{d}_{k}\right\|^{2}}<\infty$ . 对于共轭梯度算法,文献[18]给出了性质(*),当sk:=xk+1-xk变小时,βk也将变小.性质(*)[18] 对于共轭梯度算法,若任意k≥0,都有0 < γ ≤ ‖gk‖. 而且,若常数b > 1,λ > 0,使得|βk|≤b和
$\left\|\mathit{\boldsymbol{s}}_{k}\right\| \leqslant \lambda \Rightarrow\left|\beta_{k}\right| \leqslant \frac{1}{2 b}$ 都成立,就称算法具有性质(*).接下来,假设全局收敛性不在有限步发生.
引理3 若假设1、充分下降性、标准Wolfe线搜索条件均成立. 如果性质(*)成立,则dk≠0且
$\sum_{k=1}^{\infty}\left\|\boldsymbol{u}_{k}-\boldsymbol{u}_{k-1}\right\|^{2}<\infty$ ,其中$\boldsymbol{u}_{k}:=\frac{\boldsymbol{d}_{k}}{\left\|\boldsymbol{d}_{k}\right\|}$ .证 由dk≠0,gk≠0及充分下降性知,uk的定义有意义.
现定义
$\boldsymbol{\rho}_{k}:=\frac{-\boldsymbol{g}_{k}}{\left\|\boldsymbol{d}_{k}\right\|}$ 和以下式子由(3)式和(5)式,对任意k≥1,有
基于‖uk‖=‖uk-1‖=1和(9)式,得
由于βkNH+≥0,则(8)式中的ωk≥0. 此外,利用三角不等性和(10)式,可得
由Zoutendijk条件、充分下降条件和(8)式知
利用性质(*)、(11)式和(12)式,有
$\sum_{k=1}^{\infty}\left\|\boldsymbol{u}_{k}-\boldsymbol{u}_{k-1}\right\|^{2} \leqslant 4 \sum_{k=1}^{\infty}\left\|\boldsymbol{\rho}_{k}\right\|^{2}<\infty$ ,结论得证.现令
${\mathbb{N}_ + }$ 为非零自然数集. 给定正常数λ和正整数Δ,定义其中|Kk,Δλ|表示Kk,Δλ的元素个数.
引理4 若引理3的所有假设条件都成立. 算法NH+满足性质(*),则存在常数λ和k0,对任意Δ∈
${\mathbb{N}_ + }$ 和$\tilde k$ ≥k0,使得证 利用反证法论证. 假设存在Δ∈
${\mathbb{N}_ + }$ 和常数k0,对任意正常数λ和任意k≥k0,有b > 1和η > 0是性质(*)中的常数. 令λ=η,由性质(*)和(13)式,有
因此
对任意i≥1,k0≤l≤k0+iΔ,存在i′,使得
再由b > 1和(14)式得
其中c1=(2b2)Δ+1.
通过性质(*)、(6)式、(15)式和(16)式,有
其中c2=‖dk0‖. 所以,
$\sum_{k=0}^{\infty} \frac{1}{\left\|\boldsymbol{d}_{k}\right\|^{2}} \geqslant \sum_{i=1}^{\infty} \frac{1}{\left\|\boldsymbol{d}_{k_{0}+i \mathit{\Delta}}\right\|^{2}} \geqslant \sum_{i=1}^{\infty} \frac{1}{2 \overline{\gamma^{2}}+2 b^{2} c_{1}(i \mathit{\Delta}-1)+c_{2}}=\infty$ .由引理2知
$\mathop {\lim \inf}\limits_{k \to \infty } \left\|\mathit{\boldsymbol{g}}_{k}\right\|=0$ ,这与假设矛盾. 因此,原结论成立.结合引理3和4,利用文献[14]的论证方法易得下面的定理1. 限于篇幅,这里略去证明过程.
定理1 若假设1和标准Wolfe线搜索都成立. 如果算法NH+满足下面3个性质:
(p1) 对任意k≥1,有βkNH+≥0;
(p2) 充分下降性和Zoutendijk条件均满足;
(p3) 性质(*)成立,而且存在正常数M,使得θk≤M‖sk-1‖.
则算法NH+全局收敛.
-
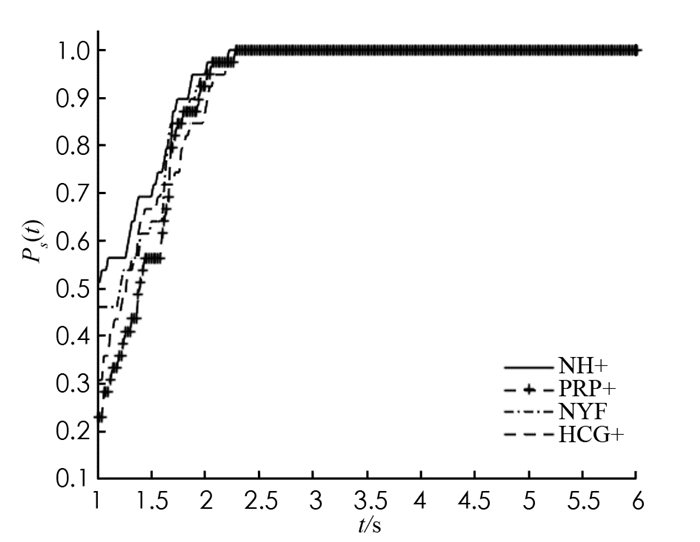
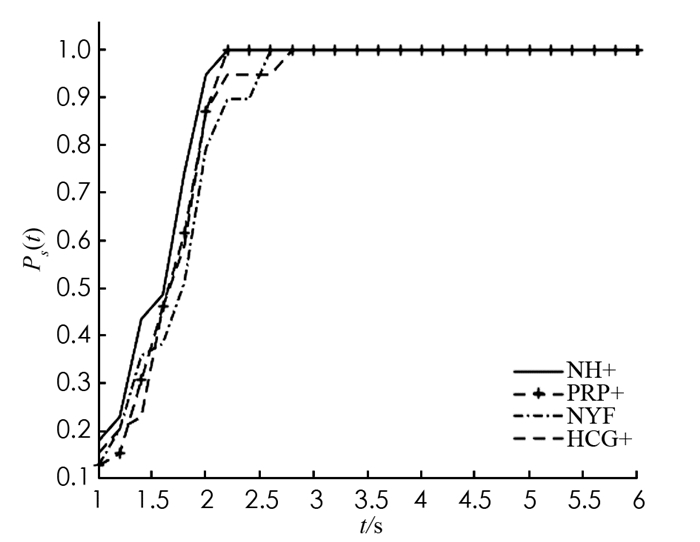
为了比较算法NH+与算法NYF[16]、算法HCG+[14]、算法PRP+[18],对文献[19]中的63个测试函数进行实验. 4种算法均利用Matlab程序实现,且在Windows 7操作系统、AMD Athlon(tm) Ⅱ Dual-Core M320 CPU和2 GB内存环境测试运行. 常数σ=0.95,δ=0.000 1. 令pk=gk. 终止准则为‖gk‖≤10-6或迭代时间超过3 600 s. 部分数值结果见表 1. 所有数值实验具体结果请参见链接https://weibo.com/2145331053/IsvzxrnEi?from=page_1005052145331053_profile&wvr=6&mod=weibotime&type=comment.
此外,利用文献[20]提出的性能理论刻画算法的计算效率和稳定性. 为此,以迭代时间、迭代次数为度量,纵轴为性能指标Ps(t),描绘出下面的性能图(图 1,图 2). 实验结果表明:NYF和PRP+在1.8 s前收敛速度都比NH+稍慢,之后都与NH+接近,并都达到稳定;HCG+比其他3种算法的收敛速度都慢;NH+一直快于其他3种算法,最终与PRP+同时稳定. 原因可能是NH+法充分利用了PRP和NYF的加速特性以及FR的良好收敛性. 因此,NH+是一个有效的算法.






 DownLoad:
DownLoad: