-
忆阻器是Chua等[1-2]提出的一种新型两端元件,考虑到电路变量之间的对称性,忆阻器的状态变量可以通过电荷和磁通之间的关系来表征. 此后,惠普实验室Strukov等[3]在纳米结构中观察到了忆阻效应,表明纳米级两端元件表现为忆阻器是可能的. 这个重要的发现做出了巨大的科学贡献,人们陆续在许多其他材料中发现了电阻开关效应. 近年来,忆阻器引起了人们的广泛关注,有大量研究致力于忆阻器建模、忆阻电路动力学分析及忆阻器在实现类脑神经计算机上的应用等[4-6].
细胞神经网络(CNN)[7]是一种实时处理信号的大规模非线性模拟电路. 与细胞自动机(CA)[8]类似的是,细胞神经网络由大量有规律、间隔的细胞组成,这些细胞通过它们最近的邻居相互通信. 在细胞神经网络中,细胞以非线性的方式与相邻细胞相互作用. 每个细胞单元由一个非线性压控电流源、一个线性电容器和几个线性电路元件电阻组成[9]. 与人工神经网络相比,细胞神经网络具有易于在硅片中实现的优点[10].
然而,随着细胞神经网络中细胞数量规模的增大,例如需要利用细胞神经网络处理大尺寸的图像时,细胞神经网络的电路结构会变得复杂,这样会给权重模板[11-12]的更新带来不便. 因此,在神经形态结构和神经网络中,利用纳米技术的忆阻器可以被用于实现突触连接,以减少面积消耗和功耗[13-14]. 由于忆阻器具有天然的记忆特性,因此忆阻细胞神经网络的信息处理能力可以进一步提高[15-16]. Itoh等[17]利用非线性无源忆阻器设计了一个细胞自动机和一个离散时间细胞神经网络. Kim等[18]利用基于忆阻器的突触构建了细胞神经网络的电路结构. 在文献[14]和文献[19]中,CNN细胞中的电阻被替换为忆阻器. 因此,CNN和忆阻器[5, 20]在多个领域都可以被认为是非常有效的工具.
忆阻神经网络的优势如下:①将纳米级尺寸的忆阻器作为人工神经突触,使得突触的高密度连接成为可能,增加了人工神经网络的连接数量;②忆阻器的阻值与流经其的磁通或电荷有关,拥有自然的信息记忆功能,因此它作为突触具备学习及存储的功能;③忆阻器的掉电不丢失性可以降低功耗;④大多数制作忆阻器的材料都和互补金属氧化物半导体(CMOS)工艺相兼容,可紧密结合忆阻器与传统电路,从而有望构成忆阻神经网络高密度集成电路的结构. 本文综合前人的研究成果,构造了新的忆阻细胞神经网络,用其代替传统细胞神经网络电路中相应的线性电阻,并构建出新型忆阻桥突触电路. 该模型除了具有传统突触桥电路的优点外,同时还简化了电路结构,可不经过转换直接输出电压信号,并且和传统忆阻突触桥电路相比,权值的更新条件更简单. 本文利用SPICE仿真证实了该模型可以实现相应权值的更新操作,并通过实验验证了该忆阻细胞神经网络可应用于图像去噪及边缘提取.
HTML
-
忆阻器是电阻可调的非线性器件,惠普忆阻器模型符合欧姆定律:
式(1)中M(t)为忆阻器的阻值:
式(2)、式(3)中D为其对应的氧化物薄膜层的总宽度,w(t)为缺氧的TiO2-X层的宽度,0≤w(t)≤D. ROFF即是当w(t)=0时忆阻器对应的高阻态,RON是当w(t)=D时对应的低阻态. μV是氧空位的平均迁移率.
由式(1)的欧姆定律,式(3)可表达为:
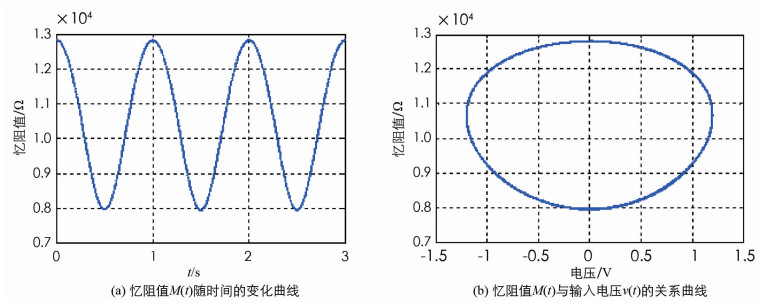
式(5)中k表示忆阻值M(t)和输入电压v(t)之间的函数关系. 设定忆阻器模型的参数为RON=100 Ω,ROFF=16 kΩ,D=10 nm,μV=10-14m2/sV. 当给其施加一个正弦激励v(t)=sin(2πt)时,忆阻值M(t)关于时间t及电压v(t)的变化曲线如图 1所示.
-
本文探讨二维M×N的忆阻细胞神经网络,即总共有M行、N列. 细胞神经网络的基本单元称为细胞,记第i行、j列的细胞为C(i,j). 其中每个细胞都同其相邻的细胞相关连,且彼此之间存在直接影响. 设作用范围是r,则一个细胞拥有一个(2r+1)×(2r+1)邻域矩阵. 本文讨论r=1的情况.
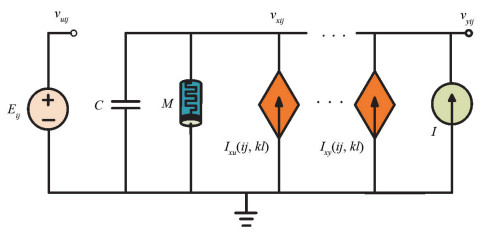
本文提出的忆阻细胞神经网络基本电路单元的原理图如图 2所示,它包含一个忆阻器、一个电容、一个独立电压激励、一个电流激励及不超过2n个的受控电流源. n表示相邻细胞的个数. 这里u,x,y分别代表输入、状态、输出. 与传统的细胞神经网络类似,每一个细胞的电路单元都含有相同的电路结构和参数[7]. 在r=1对应的细胞神经网络,各个细胞C(i,j)都能接收到来自8个邻域的输入信号,同时每个细胞C(i,j)也要提供8个输出细胞给相应的8个邻域细胞. 值得注意的是,各个细胞的总输入信号不仅来自其各个邻域细胞的输入信号,还来自其自身的输出反馈信号及独立电流源. 所以,一个细胞本身也包含于自己的邻域细胞中[7].
根据基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL),可得到单个忆阻细胞的状态方程为:
式(6)中C(k,l)∈Nr(i,j),表示(2r+1)2个相邻的细胞,即C(i,j)细胞及所有邻域细胞. 这里r的值为1. vxij表示C(i,j)的状态电压,vukl及vykl(t)表示C(k,l)的输入及输出反馈电压. Ixu(ij,kl)和Ixy(ij,kl)都是线性电压控制电流源,并满足Ixy(ij,kl)=Aij,klvykl(t),Ixu(ij,kl)=Bij,klvukl. M(t)是忆阻值,它取决于两端输入电压.
一个细胞C(i,j)的状态取决于一个独立电流源I,一个独立电压源vuij,其本身的状态vxij、输出反馈及输入控制. 输出反馈依赖于3×3的反馈模板Aij,kl,而输入控制依赖于3×3的控制模板Bij,kl,这两个模板共同决定了邻域细胞之间相互连接的权值. 权值的设定和运算可由忆阻桥电路实现.
-
在细胞神经网络对应的信号和图像处理应用中,模板有举足轻重的影响. 当细胞神经网络起不一样的作用时,其模板也应有相应的更新. 在传统的细胞神经网络电路中,权值运算用放大器和乘法器来实现,电路一旦建立,放大器的增益固定,不容易实现权值的改变.
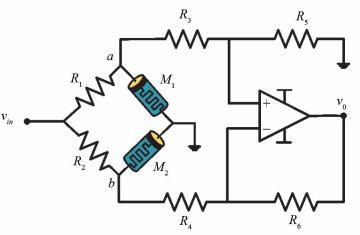
该突触模型主要由忆阻器和电阻构成,如图 3所示. 在此模型中存在两个可变器件,忆阻器M1与M2具有相反的极性,R1和R2为两个电阻. 若给该电路施加正向激励,M1和M2的阻值可以产生相反的改变. 利用减法器实现节点a与b之间的电势差. 与传统的忆阻桥突触电路相比,减法器代替了晶体管和有源负载组成的差分电路,且不再需要电流信号与电压信号之间进行转换,简化了对应的突触电路结构. 输出电压v0表示为:
令R3=R4=R5=R6,则式(7)可以表示为:
这里可以把输入v0和输出vin之间的关系表示成:
k即为该忆阻桥突触的权值,根据式(8),k可以进一步表示为:
突触权值k可以看作是与两个忆阻值相关的函数. 当M1R2>M2R1时,k大于0,突触权值为正;当M1R2 < M2R1时,k小于0,突触权值为负;当M1R2=M2R1时,k值等于0,则该电路处于稳定态,其对应的权值为零.
若令R1=R2,则k可以表示为:
此时,在突触电路模型中,其对应的权值改变的表达式可看作与M1及M2相应的方程,即:
由式(12)可知,与具有4个忆阻器的突触电路模型相比,此突触电路进一步简化了权值改变条件.
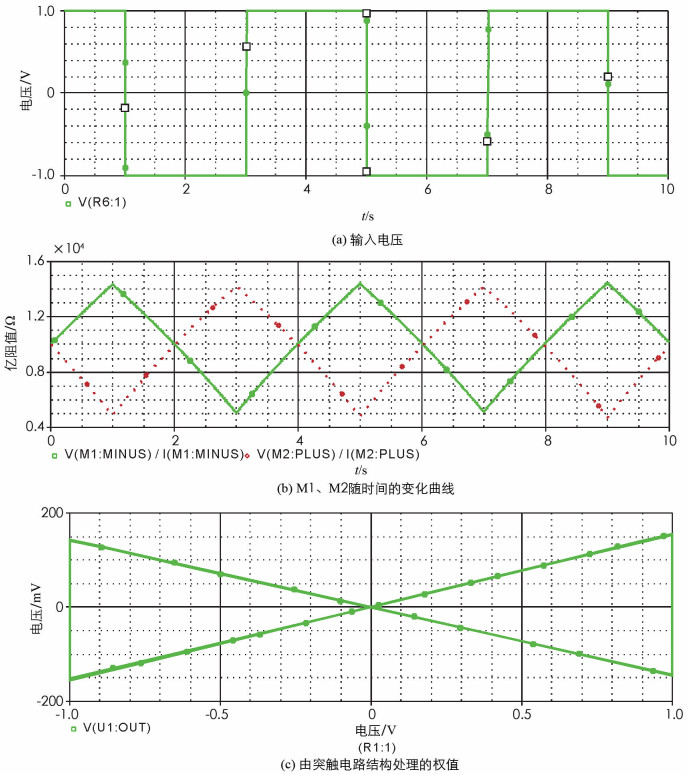
本文对该忆阻桥突触模型做了SPICE实验. 设R1=R2=30 kΩ,减法器4个阻值R3=R4=R5=R6=50 kΩ,忆阻参量RON=100 Ω,ROFF=20 kΩ,D=10 nm,μv=10-14m2/sV,并且其对应的初始条件M1(0)=M2(0)=10 kΩ. 设定仿真时间是10 s,施加的激励是周期4 s、幅值1 V的方波电压,如图 4a. 图 4b显示了忆阻桥电路中两个忆阻值和时间的关系,绿色实线表示忆阻值M1随时间变化的轨迹,红色的虚线表示忆阻值M2随时间变化的轨迹. 由图 4b可以看出,仿真结果验证了本文提出的忆阻桥突触电路能实现式(12)的结果,即能实现零、正、负的突触权值. 图 4c表征了式(7)对应的忆阻桥突触模型的权值k,横轴是输入激励,纵轴是输出信号.
-
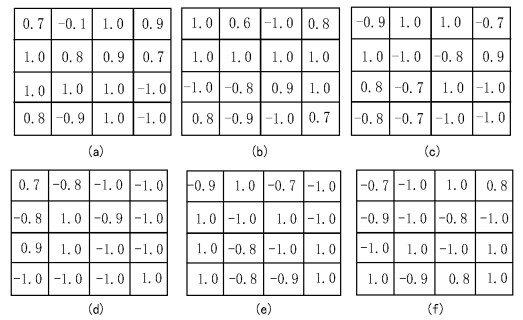
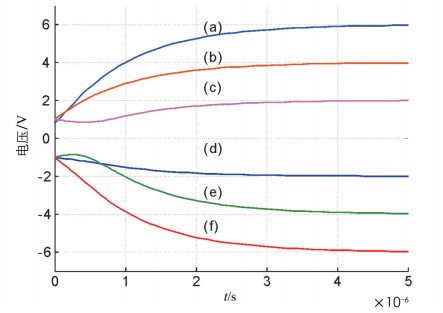
图 5为细胞C(2,2)6组不同的初始条件,细胞C(2,2)相对于图 5的6组初始条件的6个瞬时状态如图 6所示. 从图 6可以明显看出,虽然给细胞C(2,2)输入不同的初始条件,但忆阻细胞神经网络的输出状态最终都可以达到稳定状态. 设定反馈模板、控制模板和电流源的值分别为:
-
在日常生活中,输入的图像信息总是叠加一些噪声干扰. 在图像信息处理过程中,从图像中滤除该干扰最简单的方法是使用平均算子. 因此,本文选择平均算子作为去噪神经网络对应的动态规则,表示为:
另外,令控制模板和电流为:
输入一个加了高斯白噪声的指纹图片,方差σ=0.1,由图 7(a)可见,最终输出结果如图 7(f)所示. 结果表明忆阻细胞神经网络有良好的图片去噪效果,且比传统的细胞神经网络电路结构更简单.
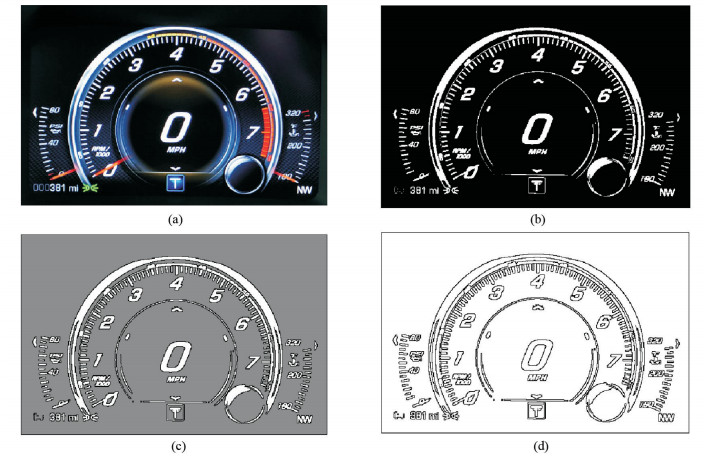
图像边缘囊括了图片大量有用的讯息,特征提取为图像处理过程中另一个关键的应用. 本文给忆阻细胞神经网络输入一张图片,如图 8(a)所示,忆阻细胞神经网络处理的结果如图 8(d)所示. 本文用的反馈模板和控制模板如式(16)所示. 由图 8可以看出,将忆阻细胞神经网络用于图像处理中,可以拥有良好的边缘选取效果.
4.1. 稳定性分析
4.2. 忆阻细胞神经网络在图像处理中的应用
-
在生命科学及信息工程中,忆阻器作为突触被广泛地应用到人工神经网络的相关研究中. 本文研究了一个新的忆阻细胞神经网络,利用忆阻器替换传统细胞神经网络电路里出现的线性电阻,并通过该突触电路用于突触权值运算. 本文改进了传统的忆阻桥突触电路,使之除了具有传统的突触桥电路的优势外,还具有更加简化的电路和简化的权值变化条件. 因此,本文提出的忆阻细胞神经网络可以减小电路尺寸,提高运算速度,电路结构具有更紧凑和更通用的优点,易于大规模集成电路的实现. 本文使用SPICE模型仿真证实了该突触结构可以实现权值运算. 另外,本文将忆阻细胞神经网络用于图像处理的去噪和边缘提取,实验结果表明其在图像处理的相关应用上具有良好的效果,并且此结构有助于促进人工神经网络进一步的硬件实现.







 DownLoad:
DownLoad: