-
目前的人口普查数据主要以不同级别的行政区划为统计单元进行统计,难以与自然、人文要素相匹配,不利于多源数据间的融合分析. 人口空间网格化具有解决行政单元边界不稳定、同级规模悬殊的效果[1],使人口空间分布更接近实际,可以实现人口与社会经济、自然资源、生态环境等的有效融合[2]. 国内外学者对人口空间网格化进行了诸多研究,利用与人口相关程度高且数据来源较为容易的相关数据进行人口网格化分析成为目前的研究目标. 赵鑫等[3]基夜间灯光、土地利用等构建指标体系后采用主成分赋权法确定权重后的广州市人口网格化; 李翔等[4]基于夜间灯光数据和空间回归模型在乡镇域尺度下对上海市常住人口格网化; 柏中强等[5]基于土地利用数据、居民点信息、DEM、夜晚灯光数据等多源数据,利用多元回归方法进行人口分布格网化. 诸多文献研究多以土地利用、居民地、交通廊道、夜间灯光数据、DEM、居住建筑斑块、通信、POI等[6-8]多源辅助数据为主进行空间网格化,但多源数据存在获取难度大,获取的多源数据常常出现时间和空间尺度不一的问题.
根据福建省乡镇域尺度的第7次人口普查统计数据以及NPP-VIIRS夜间灯光、NDVI植被指数等数据,本文利用NANI、VANUI[9]、HSI[10-11]3种灯光修正模型,采用直接面向网格的加权个案(样本加权)及加权最小二乘法(Weighted Least Squares,WLS)分别对3种修正模型的回归建模进行人口网格化,根据两两余弦相似系数、绝对距离差异系数等同一性指标互证模型合理性,并随机抽取不同比例乡镇域尺度下的网格化结果,采用MAE,RMSE,MRE和加权MAE,RMSE,MRE验证网格化精度.
HTML
-
①福建省行政区划数据:源于福建省1∶20万比例尺的栅格地图经几何校正后投影为UTM后的矢量化数据(包含县域、乡镇域等面状数据). ②网格数据:采用GIS软件“渔网”功能构建的1 km×1 km网格,与福建省区划数据相交叠加分析得到全省1 km×1 km基准网格. ③人口统计数据:福建省第7次人口普查的常住人口统计数据,往上汇总分别作为乡镇域、县域尺度的矢量数据属性值. ④NPP-VIIRS夜间灯光数据:利用2020年12个月的NPP-VIIRS月份数据合成为年均数据[12]. ⑤NDVI植被指数数据:利用2020年12个月的NDVI月份数据经算术平均合成为年均数据.
-
NPP-VIIRS、NDVI数据采用最邻近法设置为
$1 \mathrm{~km} \times 1 \mathrm{~km}$ 尺度像元后, 将夜间灯光的DN值、NDVI的DN值分别转点后, 通过空间叠加分析分别赋值基准网格. 为便于NPP-VIIRS灯光修正数据与人口建模, 将最大值规范化变换后的变量记为$x_k \cdot x_k=d n_k / n t l_{\max }, x_k \in[0, 1]$ , 当$x_k=0$ 表示为无灯光,$x_k=1$ 表示为夜间灯光饱和.
1.1. 研究区数据
1.2. 数据预处理
-
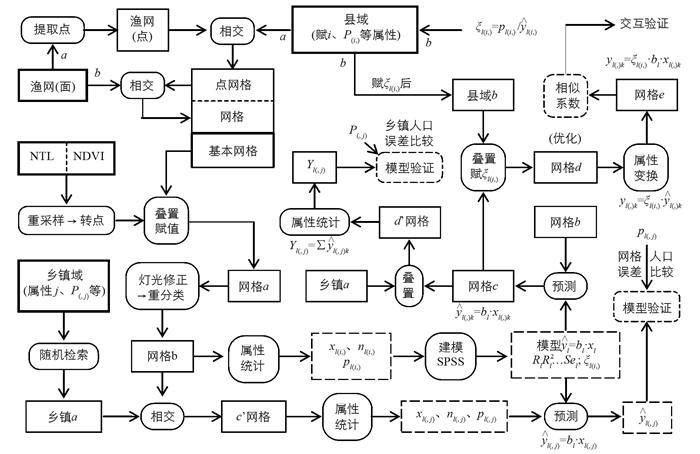
将县域用于建模与网格化,乡镇域人口数据用于模型外推与网格化结果精度验证,网格化处理流程分为4个步骤(图 1):①夜间灯光修正模型构建; ②加权个案及加权最小二乘法回归建模; ③模型外推、网格化精度验证; ④人口网格化及“零误差”优化调整.
-
由于NDVI数据的分辨率与精度优于NPP-VIIRS数据, 二者融合可有效嵈解灯光像元饱和溢出效应, 强化夜间灯光区域的内部强度差异. 为便于表达融合后的灯光修正模型, 本文将其设为
$x_l$ ($l$ 表示修正方法,$l=$ $1, 2, 3)$ , 分别代表NANI修正模型$\left(x_1\right)$ 、VANUI修正模型$\left(x_2\right)$ 和HSI修正模型$\left(x_3\right)$ , 计算方法如下.NANI修正模型记为x1,计算公式如下
VANUI修正模型记为x2,计算公式如下
HSI修正模型记为x3,计算公式如下
式中: 下标
$($ ,$) 中省略了网格继承的县域、乡镇域的 \operatorname{ID}$ 码$i$ 和$j$ , 全文下标$k, (, )k, (i, )k, (, j) k$ 均指网格ID码等于$k$ 的网格,$i, j$ 仅为强调处在$i$ 县域、$j$ 乡镇域中.$n d v i_k$ 为第$k$ 网格的NDVI的DN值;$x_{1(, ) k}$ $=x_{1(i, )k}=x_{1(, j)k}=n a n i_k$ 为$k$ 的NANI值,$x_{2(, ) k}=x_{2(i, )k}=x_{2(, j)k}=v a n u i_k$ 为$k$ 的VANUI值,$x_{3(, ) k}$ $=x_{3(i, )k}=x_{3(, j)k}=h s i_k$ 为$k$ 的HSI值. 当$n d v i_k <0.1$ 或$n d v i_k>0.9$ 时, 为不适合居住区或无常住人口区; 当$0.1 <n d v i_k <0.9$ 时, 为适合居住区中; 当$x_k=0$ 时, 说明夜间少有人类活动, 属尚无人口居住区, 网格按$x_{l(, ) k} \neq 0$ 为有人网格和$x_{l(, )k}=0$ 为无人网格重新划分为两类. -
设个案
$i$ (即县域) 的因变量$y_l$ 、自变量$x_l$ 、变量$n_l$ 的值($i$ 县域$y_l, x_l, n_l$ 的代表值,$\left.\forall i, l\right)$ 分别记为$p_{l(i, )}, x_{l(i, )}, n_{l(i, )} ; x_{l(i, )}, p_{(l, i, )}$ 代表$n_{l(i, )}$ 个有人网格的属性值, 根据图 1流程先确定权重.(1) 加权个案权重
$\gamma_{l(i, )}$ 的确定. 个案由$n_{l(i, )}$ 个有人网格平均而成, 顾及$n_{l(i, )}$ 县域人口规模差异在建模中的作用, 回归分析时将$n_{l(i, )}$ 作为$\gamma_{l(i, )}$ , 即取$\gamma_{l(i, )}=n_{l(i, )}$ 进行$x_{l(i, )}$ 和$p_{l(i, )}$ , 加权.(2) 加权最小二乘法(WLS) 权重
$\beta_{l(i, )}$ 的确定. 由于加权个案可能导致异方差, 当$n_{l(i, )}$ 值越大, 则$x_{l(i, )}, p_{l(i, )}$ , 的代表性越好、可靠性越大、精确性越高、对同方差贡献越大; 反之越小, 则$\beta_{l(i, )}=$ $n_{l(i, )} / \sum n_{l(i, )}$ .再以
$x_{l(i, )}, p_{l(i, )}$ 分别为自变量和因变量及以$\gamma_{l(i, )}, \beta_{l(i, )}$ 分别为加权个案、WLS的权重, 在网格中通过加权个案结合加权最小二乘法的回归分析, 以$n_{1, i}$ 为权重的$x_{l(i, )}$ 加权平均值与全省有人网格$x_{l(i, ) k}$ 的平均值相等,$p_{l(i, )}$ 的加权平均值分别与全省有人网格$p_{l(i, ) k}$ 及其预测值$\hat{y}_{l(i, ) k}$ 的平均值均相等, 即为无偏, 而$x_{l(i, ) k}, p_{l(i, ) k}$ 则分布在临近其平均值两侧,$p_{l(i, ) k}$ 预测值$\hat{y}_{l(i, ) k}$ 精度较高、可靠性较大, 见公式(4). 考虑到$x_{l(, ) k}=0$ 时$y_{l(, ) k}=0$ , 处理过程不勾选“在等式中包含常量”复选框.式中:bl为回归系数,表示网格xl值增/减1个单位后其yl值随之增/减bl个单位; xl为因变量、
$\hat{y}_l $ 为因变量的回归值,分别表示网格中的xl值的人口预测值/回归值. -
根据不同比例随机抽取乡镇域样本, 从不同尺度对模型进行验证, 预测乡镇人口外推, 预测风格人口网格化. 随机抽样派生乡镇
$a$ : (1)$a$ 与网格$b$ 相交得$c$ , 网格,$c$ , 属性统计得到$n_{l(, j)}$ , 及有人网格$x_l$ 平均值$x_{l(, j)}\left(x_{l(, j)}=\sum x_{l(, j) k} / n_{l(, j)}\right), x_{l(, j)}$ 代人式(4) 计算得$\hat{y}_{l(, j)}\left(\hat{y}_{l(, j)}=b_l \cdot x_{l(, j)}外推于乡镇域)\right.$ , 根据$n_{l(, j)}$ 计算$p_{l(, j)}\left(p_{l(, j)}=\sum p_{l(, j) k} / n_{l(, j)}=P_{(, j)} / n_{l(, j)}, p_{l(, j) k}\right.$ 为$j$ 的第$k$ 网格人口); (2)$a$ 与经网格$b$ 属性$x_l$ 代人公式(4) 计算派生的网格$c$ 相交得$d'$ , 网格,$d'$ , 属性统计得$\hat{Y}_{l(, j)}, \hat{Y}_{l(, j)}=\sum \hat{y}_{l(, j) k}, \hat{y}_{l(, j) k}=b_l$ -$x_{(1, j)k }$ 应用于网格化. 得到数据后代人下式验证精度.式中:MAEl,RMSEl,MREl为xl的人口预测误差,分别表示网格或乡镇域尺度人口平均或加权平均的绝对误差、方根误差、相对误差.
-
将网格
$b$ 属性$x_l$ 代人公式(4) 派生的网格$c$ , 即网格$b$ 的属性$x_l$ 的第$k$ 网格值$x_{l( , ) k}$ 代人公式(4) 得$\hat{y}_{l(, ) k}=b_l \cdot x_{l(, ) k}(\forall k)$ 赋值给新建属性$\hat{y}_{l(, )}, \hat{y}_{l(, )}$ 为上节随机抽样验证的初步网格化值. 对于回归分析, 不管个案与最小二乘法加权与否都是全局的, 都忽略了空间异质性、非平稳性, 而公式(4) 的回归系数是全省各县域共有平均值. 有学者[13-14]提出通过地理回归来解决空间异质性、非平稳性问题, 但不可否认存在一定尺度的局域稳定性, 与建模数据的空间尺度相对应, 设在县域内具同质性、稳定性, 因此根据$i$ 县域的自变量值$x_{l(i, )}$ 回代至公式(4) 中得的回归值$\hat{y}_{l(i, )}\left(\hat{y}_{l(i, )}=b_l \cdot x_{l(i, )}\right)$ 与$p_{l(i, )}$ 的不一致, 通过对每个县域确定一个回归的调节系数使$p_{l(i, )}$ 的回归值$\hat{y}_{l(i, )}$ 与$p_{l(i, )}$ 相等优化调节$\hat{y}_{l(i, ) k}$ , 使其达到全省、县域人口零误差调整. 公式为式中:
$p_{l(i, )}, y_{l(, )}, b_l, x_{l(, ) k}, \hat{y}_{l(, ) k}$ 与公式(4) 相同;$\xi_{l(i, )}$ 为$i$ 县域中回归系数的调节系数;$y_{l(, ) k}$ 为$\hat{y}_{l(, ) k}$ 的优化值.引入聚类统计量作为3种修正指数模型的人口网格化结果数据集之间的同一性指标交互验证,如下:
式中:
$l, h$ 这2种不同灯光修正模型$x_l, x_h ; y_{l(, ) k}, y_{h(, ) k}$ 分别为与$x_l, x_h$ 对应的网格$e$ 的第$k$ 网格的人口;$m$ 为全省全部网格的个数;$\theta_{l, h}$ 为余弦相似系数(其值越接近1则越相似);$d_{l, h}$ 为平均绝对距离(其值越大差异越大、反之趋向同一).
2.1. 面向网格的人口网格化处理流程
2.2. NPP-VIIRS修正模型
2.3. 加权个案的加权最小二乘法回归
2.4. 改进效果验证
2.5. 人口网格化结果优化
-
根据图 1的处理流程进行灯光像元饱和与溢出效应修正等处理后,分别进行有加权个案的WLS(改进后)与个案无加权的OLS(改进前)回归分析建模,结果见表 1所示.
由表 1可知:①在F检验中,改进后的F值与第2自由度远大于改进前,均通过了p=0.001的有统计学意义的检验; ②回归系数bl的t检验在p=0.001有统计学意义下均通过线性假设的有统计学意义检验; ③相关系数R,从改进前的0.542~0.590增至改进后的0.927~0.945,趋于1,相关性明显增大. ④模型的决定系数R2,整后为0.859~0.892,较改进前增加了2.5倍,拟合精度更高; ⑤反映模型实用价值的估计/预测标准误差Se,改进后减少210倍,精度得到提高,代表性的增强有统计学意义.
综上,3种不同方法灯光修正模型都通过了有统计学意义的检验,说明改进后比改进前效果更好.
-
按比例随机抽取的不同容量乡镇域样本验证模型外推于乡镇域与应用于网格化的结果见表 2和表 3. 由表 2可知:①网格人口绝对误差(MAE/人). 对于不同灯光修正模型xl,改进后MAE介于360~516人,不同xl没有明显差别,但都明显比改进前缩小,改进效果更有统计学意义; ②网格人口均方根误差(RMSE/人):与MAE类似,改进后的平均与加权平均分别比改进前缩小3.7~4.7倍、4.3~6.6倍,改进效果有统计学意义; ③网格人口相对误差(MRE/%):改进后分别比改进前缩小3.4~5.6倍、5.0~8.2倍,改进效果有统计学意义.
综上,改进后MAE,RMSE,MRE都小于改进前,通过了模型外推与改进方法效果的验证.
由表 3可知:①乡镇域人口绝对误差(MAE/人). 3种修正模型改进后的乡镇域MAE无明显差异,分别比改进前减少5.0~8.2倍、6.2~9.2倍,改进后明显更优; ②乡镇域人口均方根误差(RMSE/人). 改进后的平均与加权平均RMSE比改进前分别减少27.9~38.0倍与25.7~35.0倍、比改进前分别减少5.9~8.0倍与6.1~8.4倍,明显优于改进前; ③乡镇域人口相对误差(MRE/%). x1模型改进后的平均与加权平均MRE分别比改进前减少5.9~66倍与7.0~7.8倍,明显优于改进前; x2模型改进后的平均MRE只有1件样本大于46.3,其余6件中有3件小于44.62,加权平均的除1件为46.3外其他6件均小于44.62,而且改进后比改进前至减少5.0倍多,改进后优于改进前并介于x1和x3模型改进后; x3模型改进后的平均与加权平均MRE分别较改进前减少了7.3~8.2倍与7.9~9.2倍,改进后优于改进前. 综上可见在MAE,RMSE,MRE这三方面都极其明显比改进前优,且改进模型通过了网格化验证.
-
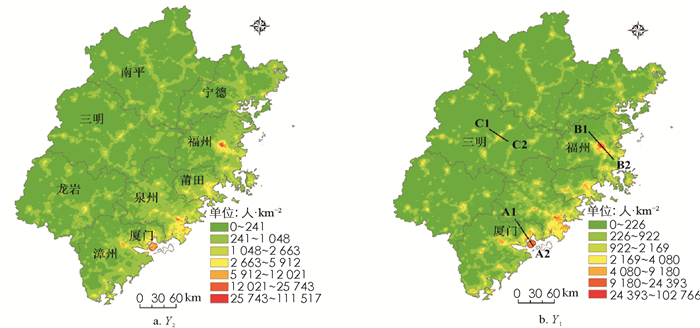
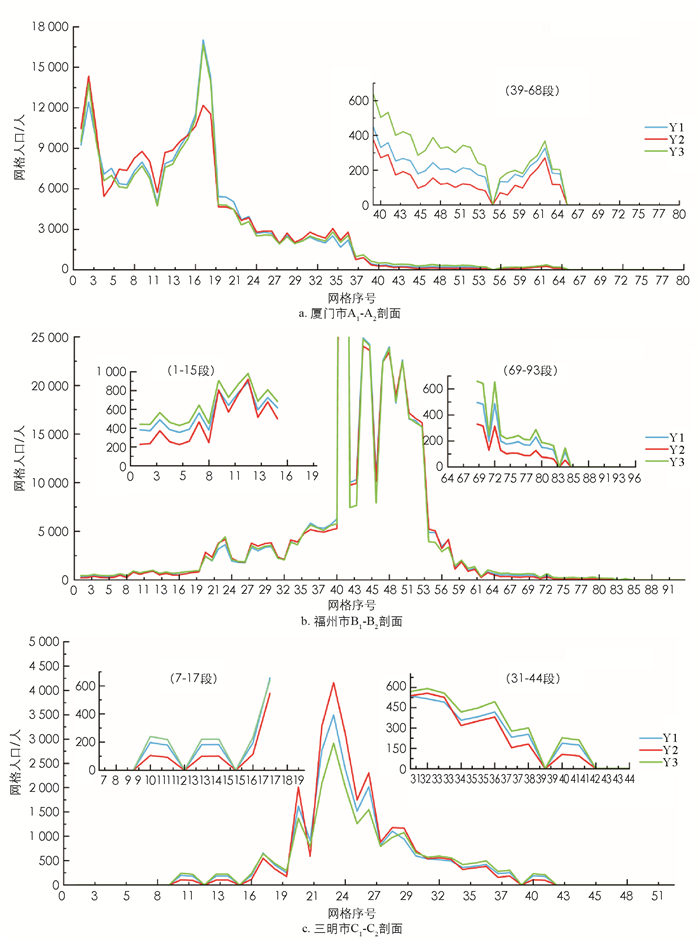
根据公式(8)-(9)对县域内人口网格化“零误差”调整,最终空间网格化结果见图 2-a和2-b所示. 由图 2可知,Y1与Y2具有高度相似的人口空间分布特征,均呈现网格人口(密度)空间分异,有统计学意义,总体上东部人口相对稠密而西部相对稀疏,并呈NE向为主与NW向为次的带状、串珠状分布,二者组合呈现为不甚规则的网状,交叉处为局域人口密集中心,其中全省的人口高值区、中心分布于闽东南沿海的福州市区、泉州市区、厦门市区等地. 其次,利用与x1,x2,x3对应的人口网格化结果绘制基于NANI模型(Y1)、VANUI模型(Y2)、HSI模型(Y3)剖面可视化折线图,见图 3-a,b,c,图 3为图 2-b横穿厦门市A1-A2、福州市B1-B2、三明市C1-C2城市中心区的网格人口(密度)表面的剖面,从中可见Y1,Y2,Y3的网格人口(密度)都是从城市中心到郊区、远郊从高值变为低值再逐渐过渡为0,与实际的人口空间分布规律相吻合,各市的Y1,Y2,Y3网格人口(密度)变化曲线不仅总体形态相似,而且剖面上相邻网格的人口增减趋势也完全一致.
将
$Y_1, Y_2, Y_3$ 的$\hat{y}_{l(i, ) k}(l=1, 2, 3 ; \forall i, k)$ 代人公式(10)计算余弦系数,$\theta_{1, 2}=0.988, \theta_{1, 3}=0.996, \theta_{2, 3}=$ 0. 981, 3种模型的余弦系数均接近于1, 可见$Y_1, Y_2, Y_3$ 两两间相似性非常大; 代人公式(11) 得平均绝对距离$d_{1, 2}=57.6, d_{1, 3}=29.1, d_{2, 3}=75.8, Y_1, Y_2, Y_3$ 两两间差异性小、同一性大.综上,从综合相似性、差异性两方面可以说明Y1,Y2,Y3趋于同一,并从图 2-a、图 2-b、图 3-a、图 3-b、图 3-c能相互印证,说明3种不同灯光修正模型的人口空间网格化结果可以互证.
3.1. 人口网格化建模结果分析
3.2. 随机样本验证模型应用与改进效果分析
3.3. 福建省人口网格化的结果
-
以NANI,VANUI,HSI 3种指数像元饱和与溢出效应修正后的模型的灯光强度为自变量,分别构建人口网格化回归模型,考察改进后与改进前的各项相关指标差异,发现改进后的加权个案及WLS建模与改进前的个案无加权的WLS建模入选模型模糊了方法改进效果,解决了人口统计单元与网格间尺度差异、统计单元间规模差异等可变面元问题,证实了改进效果的有效性,拟合优度增大了2.5倍多,预测标准误差缩小了210多倍,乡镇域随机样本的外推与网格化验证的网格人口、乡镇域人口的MAE,RMSE,MRE和加权MAE,RMSE,MRE分别缩小了3.4~8.2倍与5.0~9.2倍、3.7~6.6倍与5.9~8.4倍、3.4~8.2倍与5.0~9.2倍,提高了人口网格化精度.
3种修正模型彼此间余弦系数
$\theta_{1, 2}=0.988, \theta_{1, 3}=0.996, \theta_{2, 3}=0.981$ , 均接近1, 平均绝对距离$d_{1, 2}=$ $57.6, d_{1, 3}=29.1, d_{2, 3}=75.8$ , 两两间差异性小、同一性大, 说明不同灯光修正模型的人口网格化结果可以互证.改进方法以相关程度高的指标网格化,降低了多源数据时间和空间尺度不一和处理难度,其统计单元间、统计单元与网格间空间规模差异的方法也适用于GDP等社会经济统计数据的网格化/空间化. 此外,改进方法的加权个案等方法在时空数据(截面数据、面板数据)的一些分析方法中,也可以借鉴参考.






 DownLoad:
DownLoad: