-
随着信息化时代的到来,大数据的应用越来越广泛,同时也不可避免地出现了异质性问题,表现出异方差特性. 而当数据中存在异方差误差或异常点时,变量选择的结果将不再稳定. 目前变量选择方法主要分为非贝叶斯方法和贝叶斯方法. 基于惩罚函数的变量选择是非贝叶斯方法的主流[1-9],最常见的包括LASSO(Least Absolute Shrinkage and Selection Operator)及其改进方法,如:EN(Elastic Net)、自适应LASSO(ALASSO)、组LASSO、SCAD(Smoothly Clipped Absolute Deviation)、MCP(Minimax Convex Penalty)、最小绝对偏差LASSO[7]等. 尽管非贝叶斯方法已经取得了不错的成果,但这类方法都不能提供令人满意的标准差估计.
文献[1]表明当回归参数具有独立且相同的拉普拉斯先验时,LASSO估计可以解释为后验众数估计. 因此,基于该联系和贝叶斯思想,文献[10]提出了贝叶斯LASSO(BLASSO)并构造了全贝叶斯分层模型和相应的采样器. 文献[11]证明在预测均方误差方面,贝叶斯LASSO的表现与频率派LASSO相似甚至在某些情况下更好. 基于文献[10-13]的研究,本文将贝叶斯LASSO与异方差误差先验相结合,以实现稳健的变量选择与系数估计,同时该法能自动产生各参数的置信区间.
HTML
-
考虑以下线性回归模型
其中:Y为n×1维的因变量,X为n×p维的解释变量,误差ε服从异方差的多元正态分布,V =diag(V1,…,Vn),则该模型的似然函数如式(2)所示
将该模型的似然函数与各参数的先验分布相乘,可得联合后验分布为
基于式(3),可得β的全条件后验分布服从均值为B -1 X T V -1 Y,方差为σ2 B -1的多元正态分布,其中:B = X T V -1 X + D τ-1;σ2的全条件后验分布服从形状参数为
$\frac{n}{2}+\frac{p}{2}+\alpha$ ,尺度参数为$\frac{(\boldsymbol{Y}-\boldsymbol{X} \boldsymbol{\beta})^{\mathrm{T}} \boldsymbol{V}^{-1}(\boldsymbol{Y}-\boldsymbol{X} \boldsymbol{\beta})}{2}+$ $\frac{\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{D}_{\boldsymbol{r}}^{-1} \boldsymbol{\beta}}{2}+\gamma $ 的逆伽马分布;$\frac{1}{\tau_j^2} $ 的全条件后验分布服从形状参数为λ′=λ2,均值参数为$\mu^{\prime}=\sqrt{\frac{\lambda^2 \sigma^2}{\beta_j^2}}$ 的逆高斯分布;文献[12]得出V的全条件后验分布服从以下形式的卡方分布式中ei项为向量e = Y - Xβ的第i个元素,V -i=(V1,…,Vi-1,Vi+1,…,Vn),i=1,…,n. 根据各参数后验分布可构造出稳健贝叶斯LASSO的Gibbs采样算法:
算法1:稳健贝叶斯LASSO的Gibbs采样器 输入:Y,X,迭代次数Tdraw,预热次数Tomit,初值β(0),σ(0)2,τ(0)2,V(0) 输出: $\hat{\boldsymbol{\beta}}, \hat{\sigma}^2, \hat{\tau}^2, \hat{\boldsymbol{V}} $ 1:k←1 2:当k≤Tdraw 3: 从后验分布p(β|Y,X,σ(k-1)2,V(k-1),τ(k-1)2)中抽样并记为β(k) 4: 从后验分布p(τ2|Y,X,β(k),σ(k-1)2,V(k-1))中抽样并记为τ(k)2 5: 从后验分布p(σ2|Y,X,β(k),V(k-1),τ(k)2)中抽样并记为σ(k)2 6:从后验分布p(V|Y,X,β(k),σ(k)2,τ(k)2)中抽样并记为V(k) 7:k←k+1 8:结束 9:删去前Tomit轮样本,取后Tdraw-Tomit轮样本计算各参数的后验平均值作为估计值 -
关于超参数λ2的选取,借鉴文献[10]提出的基于边际最大似然的经验贝叶斯法,具体算法如下:
1) 令k=0并设初值为
$ \lambda_{(0)}=\frac{p \sqrt{\hat{\sigma}_{\mathrm{wLS}}^2}}{\sum\limits_{j=1}^p\left|\hat{\boldsymbol{\beta}}_{\mathrm{wLS}}^2\right|}$ ,其中$\hat{\sigma}_{\mathrm{WLS}}^2 \text { 和 } \hat{\boldsymbol{\beta}}_{\mathrm{WLS}}^2$ 为以普通线性最小二乘估计残差值的绝对值的倒数为权重的加权最小二乘估计值;2) 令λ=λ(k)并利用上述Gibbs采样器从β,σ2,τ 2,V的后验分布中生成第k轮样本;
3) 利用第k轮样本近似计算更新
$\lambda_{(k+1)}=\sqrt{\frac{2 p}{\sum\limits_{j=1}^p E_{\lambda_{(k)}}\left[\tau_j^2 \mid \boldsymbol{Y}\right]}}$ 并令k=k+1;4) 重复步骤2)-3)直至所需的收敛水平.
由于经验贝叶斯法需要多次Gibbs采样,因此该法计算量极大. 文献[14]提出了一种基于随机近似的单步方法作为替代,该方法可以仅使用单次Gibbs采样器来获得超参数的极大似然估计,从而极大减少计算量. 该法首先作变换λ(k)=es(k),具体算法如下:
1) 令k=0并设初值为s(0)=0,θ (0)=(β (0),σ(0)2,τ (0)2,V (0));
2) 从Ks(k)(θ(k),·)中生成θ(k+1),其中Ks为联合后验分布p(· |Y,s)的Gibbs采样器的马尔科夫核;
3) 令
$s_{(k+1)}=s_{(k)}+a_k\left(2 p-\mathrm{e}^{2 s_{(k)}} \sum\limits_{j=1}^p \tau_{j, (k+1)}^2\right) $ 令k=k+1;4) 重复步骤2)-3)直至所需的迭代次数.
其中{ak,k≥0} 为一个非降的正数序列,并满足以下性质
1.1. Gibbs采样器
1.2. 超参数选取
-
本节将评估异方差误差先验下稳健贝叶斯LASSO的实验特性与优点. 根据式(1)生成数据,令X=[ιn,X′],ιn为n维的单位向量,X′= [X1,X2,…,Xp-1]为多元正态分布N(0,Σ)生成,其中Σij=0.5|i-j|. 为了考虑系数向量不同的稀释度,所有模拟均设置n=100和p=50并令非零系数的个数q∈{10,20}. 此外,为了测试收缩的适应性,一半的非零系数从正态分布N(0,1)中生成,另一半非零系数从正态分布N(0,5)中抽样,从而使得一半的非零系数接近于0,另一半的非零系数则表现出更大的变化,剩余系数则设置为0. 每次模拟均使用5 000次迭代并取后2 500次抽样计算各参数的后验均值作为估计值,为了避免偶然性,模拟均重复100次. 为了考察所提方法对异常值的稳健性,本文考虑了4种不同的ε.
例1(异方差误差):为了生成异方差误差,对于样本量n按照文献[15]生成随机组,其中组的个数由均匀分布U(3,20)抽样得出. 如果组个数大于10,则将该组所有样本的方差设置为等于组个数,否则将方差设置为组个数倒数的平方,并令ε的第i个元素为
其中:σi为第i个观测样本的标准差,ξi来自独立同分布的标准正态分布N(0,1).
例2(污染分布):ε服从污染分布,其中前90%来自标准正态分布,后10%服从标准柯西分布.
例3(柯西分布):ε服从标准柯西分布.
例4(拉普拉斯分布):ε服从标准拉普拉斯分布.
为了衡量系数估计与变量选择的性能,本文采用均方误差(MSE)与平衡准确率(BAR)作为指标. 平衡准确率能综合衡量变量选择方法正确选择、错选、漏选变量的个数,其计算公式如下
其中TP,TN,FP,FN分别表示真阳性、真阴性、假阳性和假阴性的数量.
将本文提出的稳健贝叶斯LASSO方法简记为RBLASSO. 表 1列出了不施加异方差误差先验下几种常见方法与RBLASSO的实验结果,其中每项指标为基于100次模拟的平均值. 值得注意的是,贝叶斯方法的变量选择结果基于参数的95%置信区间. 若95%置信区间含0,则可认为该参数被识别为0.
从模拟结果可得,本文方法在大多数情况下都具有较好的综合表现,其中当误差分布为异方差时RBLASSO的各项性能指标均为最优. 根据对比可得,当非零系数的个数q增大时,即系数向量越密集时,每种方法的估计值往往会稍差,这是因为需要用相同数量的观测值估计更多的非零参数. 当误差分布服从标准柯西分布,即例子3时,不施加异方差误差先验下的贝叶斯LASSO的
$\operatorname{MSE}(\hat{\boldsymbol{\beta}})$ 相比其他误差分布大得多,而RBLASSO依然能保持较好的系数估计与变量选择能力,甚至在q增大时$\operatorname{MSE}(\hat{\boldsymbol{\beta}})$ 反而减小,这表明了施加异方差误差先验对抵抗异常值具有重大作用.
-
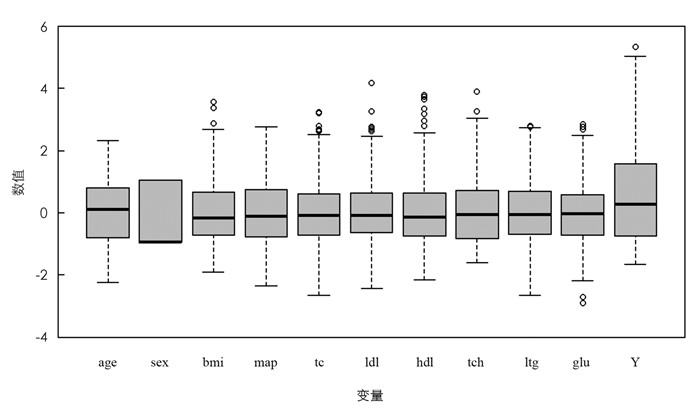
将本文提出的稳健贝叶斯LASSO方法应用到糖尿病数据集中,该数据集由文献[16]提供,共有442个样本和11个变量,其中10个解释变量分别为年龄(age)、性别(sex)、体重指数(bmi)、平均血压(map)及6种血清测量(tc,ldl,hdl,tch,ltg,glu),因变量为基线点一年后疾病进展的定量测量. 本文所使用的数据集来自R包care,所有变量均已标准化使得均值为0、方差为1. 为了研究所提方法的稳健性,随机选取20%的样本在因变量上加上噪音c,其中c取为3倍的因变量标准差,并随机划分70%的数据集作为训练集,剩余30%作为测试集. 评估指标采用预测均方误差(MSE)与中值绝对预测误差(MAPE).
图 1为该数据集各变量的箱线图,初步可得解释变量和因变量均存在异常值;图 2为学生化残差与帽子统计量关系图,其中圆圈面积与观测点的Cook距离成正比,垂直两条虚线分别为两倍和三倍平均帽子值的参考线,水平两条虚线分别是学生化残差为0及2的参考线,进一步分析可得该数据集中样本295和305为离群点,样本323和354为高杠杆值点,若以
$\frac{4}{n-k-1} $ 为Cook距离的阈值则有35个强影响点.各模型估计结果如表 2所示,其中标粗体的系数估计值代表其置信区间含0. BLASSO和RBLASSO均排除了7个相同的非重要变量,而LASSO和ALASSO仅排除了4个非重要变量,且这4个非重要变量均为4个模型所排除的共同变量,分别为sex,ldl,tch,glu. 根据MSE和MAPE,本文所提方法的预测误差最低. 此外,由图 3可得相比BLASSO,施加了异方差先验的RBLASSO具有更短的置信区间. 因此,所提方法的结果应具备更高的可靠性.
-
文献[17]数据集包含了315名患者,均在3年内进行过活检或切除肺、结肠、乳腺、皮肤、卵巢或子宫的非癌病变,选取其中的273名女性患者作为研究对象. 该数据集共有11个变量,10个解释变量分别为年龄(age)、吸烟状态(smokstat)、Quetelet指数(quetelet)、维生素使用(vituse)、每天摄入的卡路里数(calories)、每天摄入的脂肪克数(fat)、每天摄入的纤维克数(fiber)、每周摄入的酒精饮料数量(alcohol)、胆固醇摄入量(mg/天,chol)、膳食β-胡萝卜素消耗量(mcg/d,betadiet),因变量为血浆β-胡萝卜素(ng/ml). 所有变量均已标准化使得均值为0、方差为1,随机划分70%的数据集作为训练集拟合模型,将剩余30%作为测试集并通过计算预测均方误差(MSE)与中值绝对预测误差(MAPE)来评估模型的预测能力.
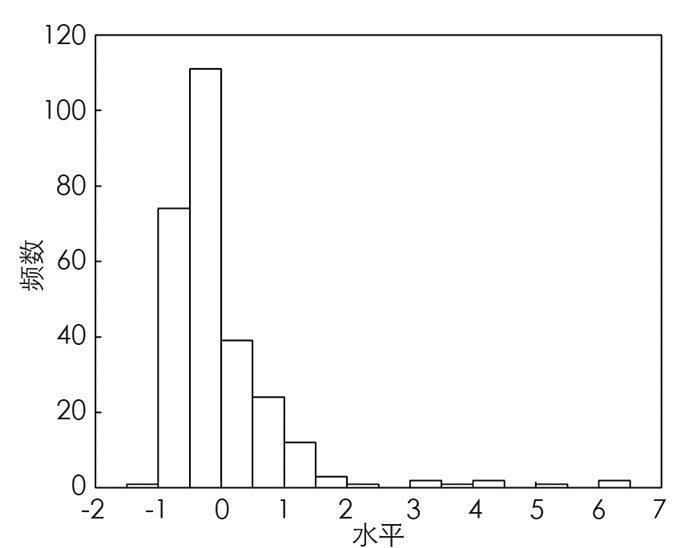
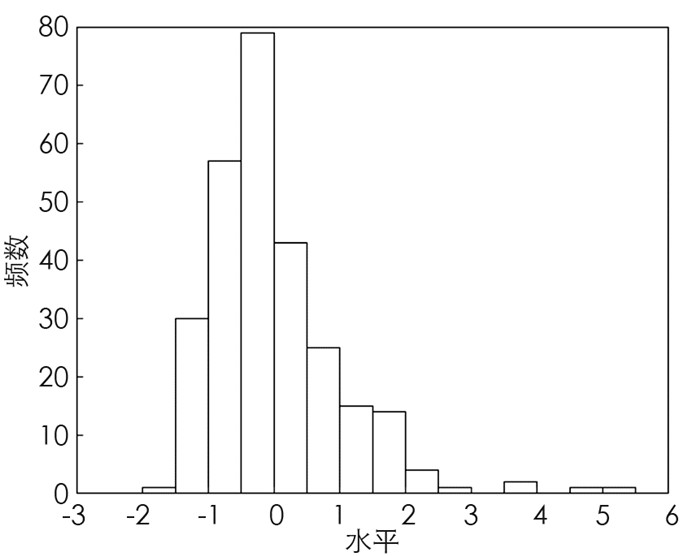
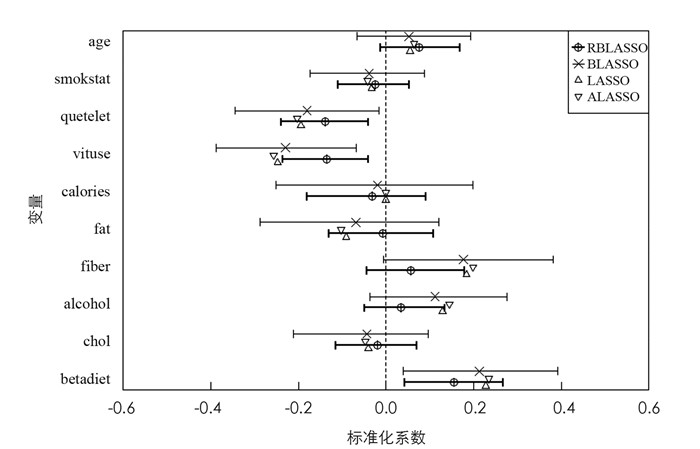
图 4和图 5分别为血浆β-胡萝卜素和胆固醇的直方图,由图可得这两个变量均含有异常值. 将各模型应用于该数据,估计结果如表 3所示,其中BLASSO和RBLASSO均认为quetelet,vituse和betadiet为重要变量,而LASSO和ALASSO仅排除了calories变量. 尽管RBLASSO的MAPE不是最低,但与MAPE最低的BLASSO差距甚小,且RBLASSO的MSE远低于其他方法,综合来说RBLASSO模型的预测能力最优. 此外,从图 6可得RBLASSO明显比BLASSO具有更短的置信区间,估计精度更高.
3.1. 糖尿病数据集
3.2. 血浆β-胡萝卜素水平数据集
-
本文通过将异方差误差先验引入贝叶斯LASSO,提出了贝叶斯LASSO的稳健模型并建立了相应的贝叶斯分层模型与Gibbs采样器,从而提高了对异常值及异方差误差的稳健性. 数值模拟和实证分析表明当存在异常值或异方差误差时,该方法能实现较简洁的模型与较低的误差,从而实现稳健的变量选择. 此外,该模型立足于贝叶斯思想,能方便地得到估计值的置信区间,从而弥补了LASSO类方法不能给出较好可信度评估的劣势.








 DownLoad:
DownLoad: