On Teaching Design of Curriculum Ideological and Political Education in Basic Courses of College Mathematics——Take the Ideological Course of Probability Theory and Mathematical Statistics as an Example

习近平总书记在2016全国高校思想政治工作会议上的讲话^[1]吹响了“三全育人”，加快课程思政建设的号角，也为新时期的大学数学基础课程教学提出了新要求.

概率论与数理统计作为工科类专业的大学数学公共基础课，覆盖面广，理论和方法有着十分广泛的应用，其思想也渗入到各个学科，具有较强的课程思政研究背景和要求.概率论主要研究随机现象及其数量规律性，内容兼具传统的数学课程重“理”重“术”的特点和独有的随机性量化分析，能有效培养学生数学素养和创新意识.从思政背景来看，概率论所蕴含的偶然与必然、矛盾与对立、现象与本质的辩证唯物主义思想能引导学生从事物的两面性去认识世界，有利于培养正确的人生观和价值观.统计部分主要研究如何通过收集分析数据对具体问题作出推断和预测，这与我们的生活密切相关.可以这样说，凡是有数字的地方，都离不开数理统计. “从实践中来，用数据说话”，这正是数理统计所蕴含的人生哲理，对培养学生实事求是的社会主义核心价值观有着重要的意义.

课程思政不是一门或一类特定的课程，也不单纯等于课程加思政，而是以知识传授为基本出发点，充分挖掘课程中的隐形教育资源，合理融合思想政治教育的新模式、新理念.但“硬核”的数学课程，以计算、逻辑推理为主，很难与思政教育水乳交融.因此，我们有必要结合教学实际，推动概率论与数理统计的课程思政研究.近年来，已有大量教师结合不同学校学科实际情况开展了数学基础课程思政的实践和探索，如：文献[2]探讨了在数学分析课程中融入课程思政的途径; 文献[3]研究了大学数学课程中开展课程思政的方法和特点; 文献[4]提出了高等数学中的大量数学思政案例等.本文将从以下几个方面构建概率论与数理统计课程思政的逻辑框架.

教学是一项需要师生共同完成的人才培养活动，课程思政亦是如此.从教师层面，首先，坚定的社会主义核心价值观和扎实的专业知识是大学数学教师必须具备的基本素质，“学高为师，身正为范”，方能潜移默化，引导学生树立正确的人生观、价值观; 其次，教师要提高自身落实课程思政的觉悟和素质.在数学基础课程的教学中，教师往往会把重点放在理论知识的讲解，认为数学课程和思想政治是两条平行线，无法相交，缺乏进行思政教育的主观能动性.事实上，数学是一切高科技的基础，中华民族有着悠久的数学历史和卓越的成果.在教学过程中积极启发和引导学生去感受数学魅力和文化底蕴，就能帮助学生坚定文化自信，建立实事求是、严谨认真的价值观.

从学生层面，新时代的大学生有较强的自我意识，价值取向务实功利，大一高等数学课程的学习使部分同学产生了大学数学课程难，对生活无用论等先入为主的认识.在针对本校2019级学生的对概率论与数理统计课程的感兴趣程度的课前问卷调查中，仅20%的同学选择很感兴趣，而选择无所谓和不感兴趣的同学多达50%.合理的课程思政能直达内心去激发学习热情，帮助学生树立对本课程的正确认识，使学生从感兴趣到主动学习，达到数学能力及学习品格和意志的双提升.

固化“术道结合”的教学目标是确保课程思政理念下的概率论与数理统计教学顺利实施的根本出发点.在知识目标上，要让学生掌握基本概念、方法和理论等传统的数学元素以及随机性量化分析方法，数据拟合检验等独特的教学内容及全新的思维模式.在能力目标上，针对大数据背景，结合学生专业情况合理向实际应用倾斜.要求学生能充分结合数学建模思想，有基本解决实际概率问题和数据分析处理能力.此外，课程思政模式下的教学还应凸显育人目标，即充分延拓本课程的数学内涵，让学生体会概率思维，并通过思政案例培养学生形成正确的人生观和价值观，实现课程工具理性和价值理性的统一.事实上，育人目标对其他目标起到提纲挈领的作用，是大学课程教学的终极目标^[5].最后，教学的目标不应只针对学生，对同为教学参与者的教师来说，应在每一次的教学过程中感悟本课程的知识和价值发展，实现自身素质的提高.

当今社会，教学资源和内容的获得变得多元化.传统纸质教材与网络平台资源的充分融合使教学内容更加丰富.在深挖课本的同时，整合网络教育资源和同期各种热点问题，这本身就蕴含着与时俱进的思政思想，也是实现教学相长的重要途径.以本课程重点内容区间估计为例. 2020年1月新冠疫情爆发初期，发表在知名医学期刊《柳叶刀》上最早确认新冠肺炎具有“人传人特征”的论文中就估计出2019-nCoV的基本再生数95%的置信区间为[3.6，4.0].结合本节教学内容，引入变量X表示再生基本数，上述结论可表示为P{3.6≤X≤4.0}=1-5%=95%，由此引出95%为置信度，3.6为置信下限，4.0为置信上限，[3.6，4.0]为置信区间等专业术语，相信学生不仅能直观理解基本概念，更能从这场全民参与的共同胜利中体会民族自豪感，从而激发学习兴趣和热情，由此达到课程思政的目的.

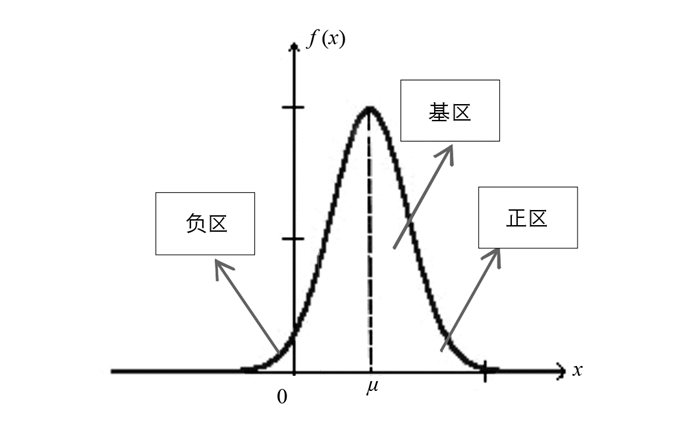
再以3种典型的连续型随机变量教学内容为例.对均匀分布U[a，b]，其密度函数为 $f(x) = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{{b - a}}}&{x \in [a, b]}\\ 0&{x \notin [a, b]} \end{array}} \right.$，随机变量X落在子区间上的概率只依赖于子区间的长度，与子区间的位置无关.若将密度函数作为努力系数，区间长度作为付出度，均匀分布对应了付出与成功成正比的公平公正原则，由此引导学生培养积极正向的学习态度；对指数分布E(λ)，其分布函数为 $F(x) = \left\{ {\begin{array}{*{20}{c}} {1 - {{\rm{e}}^{ - \lambda x}}}&{x > 0}\\ 0&{x \le 0} \end{array}} \right.$，可以证明指数分布具有“无记忆性”，即对任意s>0，t>0，都有P{X>s+t|X>s}=P{X>t}.此公式表明若过去的s h不尽人意，不必气馁，努力(s+t) h，仍能提升成功概率.往日不可谏，来者犹可追，可针对性的鼓励部分差生重拾信心，把握现在.而对正态分布N(μ，σ²)，密度函数为 $f(x) = \frac{1}{{\sqrt {2\pi } \sigma }}{{\rm{e}}^{ - \frac{{{{(x - \mu )}^2}}}{{2{\sigma ^2}}}}}$，-∞ < x < +∞，该密度函数如图 1所示.

此图像以对称轴x=μ为中心，标准差σ为半径分为基区、负区和正区，三区各有权重，协同而立.由此引导学生在学习生活中，要立足基区，放眼负区和正区，培养学生有的放矢，集中主要精力解决主要问题.

此外，我国概率论与数理统计的发展史，是中华民族传统文化与概率思维不断碰撞的成长史，也是数学家们不惧艰难，勇于挑战的斗争史.在教学内容中，合理增加“歧路亡羊”“三人行，必有我师焉”等典故，可呈现概率与传统文化的完美结合; 也可从许宝騄、王梓坤等概率学先驱的学习和成长故事中，感受数学家献身祖国、献身数学的奉献精神，从而引出学生的家国情怀和社会责任感，让思政教育深入人心，激励学生为实现中华民族的伟大复兴而自觉努力学习.

教学过程是实施课程思政的核心环节.教学过程中的课程思政必须遵循课程自身规律.本课程教学过程中的课程思政主要集中于教师对教学内容的思政引导，包括数学家、数学史的介绍，定义定理的发散，经典案例的引入，学生统计实验的探究与体会等.以第一节课为例，教师应首先对本课程起源、发展、应用等做相关介绍，如概率起源于费马和帕斯卡的7封解决贵族博弈点数问题的信件，不仅能有力驳斥数学对生活无用的错误思想，还能让学生感受数学家攻坚克难、脚踏实地的数学精神和优良品质，让课程思政合理融入课堂教学，润物无声.其次在介绍概率论和数理统计的基本内容时，可强调二者相辅相成，课程之间的相互融合能更有利于学科的发展.由此启发同学之间相互合作，建立小组制的学习模式，共同完成课程设计、答疑、小论文等相关问题，利于学生养成友善团结，协同发展的优良品质.

此外，疫情期间线上教学也引发了对教学过程新的思考.线上教学能获得更多的数据资料和思政元素，使教学过程更加多元化.如在学习统计部分的基本概念时，可利用教学平台上某116人的教学班在4月22日到5月22日间的到课人数及出勤率(表 1).

由表 1设计出勤率X的样本均值 $\bar X = \frac{1}{9}\sum\limits_{i = 1}^9 {{x_i}} = 96.7\% $，样本方差 ${S^2} = \frac{1}{{9 - 1}}\sum\limits_{i = 1}^9 {{{({x_i} - \bar X)}^2}} = 0.051\;7\% $.该教学过程设计既巩固了基本概念，锻炼学生的动手能力，又贴合统计主题让学生积极参与课堂感受让数据说话的魅力，同时还用数据提醒学生积极到课，对组织管理较为松散的线上教学起到监督的作用，由此达到课程思政的目的.此外，文献[6]指出，大部分学生能在线上教学中感受到职业道德和风险意识等方面的思政教育，这也是线上教学的思政体现之一.

合理有效的教学手段与方法是实施课程思政的重要载体.针对本课程普遍的逻辑性.理论性和实用性等特点，可多采用研究型教学法和案例教学法相结合的形式，应用启发式、引导式的教学手段，结合每个章节给出相关数学建模实例或衍生问题，让学生自己查阅相关资料，借助统计软件，提出解决办法.以正态分布的密度函数的学习为例，可给出积分计算问题 $\int_a^b {{{\rm{e}}^{ - {x^2}}}} {\rm{d}}x$让学生进行思考.由于该原函数的特殊性，学生可利用高等数学中Γ函数的知识去思考，也可借助数学软件matlab，mathmatica等进行计算，还可结合本节知识利用连续型随机变量概率的计算方法进行反解.在此过程中，学生可以感受数学各分支之间的相互交融，理解学术研究的整个过程，提升创新意识，培养探知未来的勇气，这也从侧面巩固了课程思政的理念.

建立以学生为主的多元评价体系有利于更好进行本课程相关课程思政模式的探索.以单元、期中、期末成绩测验和课程思政小论文、实际应用小论文为切入点，对平行班级采取表 2所示评价体系开展过程性对比研究.

同时还应结合不同班级整体学习态度、课堂表现、考试认真程度、作业完成情况等综合对比分析，为概率论与数理统计的课程思政的系统化提供有力支撑.