The Development of Research on Pedagogical Content Knowledge and Its Value

舒尔曼1986年发表的《理解者：教学中的知识增长》是教师知识研究领域公认的经典之作。这篇文章首次对学科教学知识进行了系统的界定，认为学科教学知识主要包括两层含义：(1)学科教学知识是学科思想最有效的呈现形式，是其最有力的类比、显示、例证、解释和演示；(2)学科教学知识是对一些困难知识的处理技巧，由于不同年龄和不同背景的学生对学习内容持有不同的概念和前概念，所以教师需要具备帮助学习者理解困难知识的能力^[1]。

学科教学知识概念提出后，引发了一系列经验研究。最初的研究大部分是质性研究，即通过具体的案例探讨学科知识与学科教学知识之间的关系，并且对学科教学知识进行细致的分类，描述学科教学知识对教师课堂教学的影响。这些研究主要聚焦在两个方面。

一是基于具体的学科内容来阐述学科知识与学科教学知识之间的关系，以此探讨学科知识对学科教学知识的影响。鲁哈马·埃文(Ruhama Even)选择函数作为研究内容，通过对新手教师和成熟型教师进行比较研究后指出，教师自身具备的函数知识，对教师在课堂中如何向学生解释函数的定义、怎样确定教学重点以及选择什么样的方式帮助学生理解函数，都有明显的影响^[2]。因此，学科知识对学科教学知识具有决定性的作用。斯登(Mary Kay Stein)、巴克斯特(Juliet A. Baxter)和莱因哈特(Gaea Leinhardt)以一位具有18年教龄的小学数学教师为个案，分析了该教师的25节函数和图形的课堂视频。研究结果表明，与专家型教师相比，普通教师的学科知识结构化程度较低，因此，普通教师往往拘泥于事物的表象，难以领会知识的本质，在课堂教学中不能清晰而富有逻辑地解释函数的概念及其应用，也不能准确把握学生在理解函数过程中可能遇到的困难，课堂教学流于表层^[3]。

二是对学科教学知识进行进一步细化研究，探讨学科教学知识对教学与学业成绩的影响。彼得森(Penelope L. Peterson)等人从学科教学知识中分离出学科教学信仰，提出了检验学科教学信仰的理论框架，并以对39位教师的调查为依据，探究了学科教学信仰对学生学习成绩的影响^[4]。卡彭特(Thomas P. Carpenter)等人提出学科教学知识测量的3个维度：(1)教师对不同类型数学问题的认识程度；(2)教师对学生解决数学问题所应用策略的了解程度；(3)教师对解决学生不同类型数学问题所应用的策略的辨析水平。基于这3个维度，研究者对教师的学科教学知识进行了调查，并分析了教师的学科教学知识对学生学业成绩的影响^[5]。这两项研究都把学科教学知识作为一个重要变量，分析它对学业成绩的影响，以此寻找学科教学知识与学业成绩之间的内在机制。但是，这两项研究对学科教学知识的界定和测量仍处于初步发展阶段。

除上述针对数学学科的研究之外，还有对英语、科学、社会研究等科目教师教学知识的经验研究。这些研究大多采用质性研究方法，主要是对教师的个案研究、专家与新手教师的比较研究等。美国学者鲍尔(Deborah Loewenberg Ball)指出，在1986年至2008年间学科教学知识被引用1 300多次，平均每年被引用60多次。但是，如此高频率的引用和研究并没有推动该领域的深入发展。很多研究只是沿用此概念，并没有回答这个概念的真实内涵以及在具体的学科教学中如何体现等问题。学科教学知识的真实意义被掩盖，不能有效地帮助我们认识教师知识的真实状态。此外，对学科教学知识的经验验证并未有明显的进展，客观测量学科教学知识的量表未被研制出来。学科教学知识究竟对教学质量和学生学业成绩有怎样的影响，还缺乏深度的量化研究^[6]。

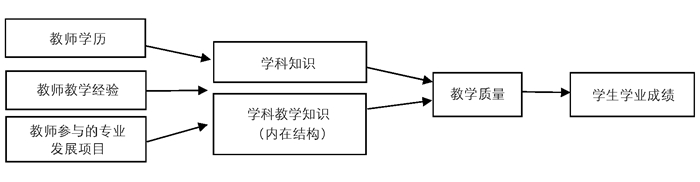
针对上述对学科教学知识研究的质疑，以密歇根大学鲍尔为首的研究群体对学科教学知识进行了细致深入的实证研究，把学科教学知识既作为因变量，也作为自变量，通过精确测量，探讨了学科教学知识的影响因素以及对其教学质量和学生学业成绩的影响。这一系列研究主要围绕3个方面展开：一是学科教学知识的构成，即是否存在一个具体的指标可以来测量学科教学知识；二是影响学科教学知识的要素，即从教师学历、教师教学经验和教师参与的专业发展项目等方面，探讨学科教学知识受哪些因素的影响；三是学科教学知识的作用，即通过数据分析来验证教师的学科知识、学科教学知识对教学质量和学生学业成绩是否有实质性的影响。这3个方面构成一个经验模型，具体如图 1所示。

2004年以来，鲍尔和希尔(Heather C. Hill)连续发表多篇文章，对学科教学知识结构进行了新的分析，并开发了学科教学知识测量量表。希尔等人把数学教师教学所需的知识分为两类：一类是内容知识，主要包括一般的数学知识和专门的数学知识，这与舒尔曼所指的学科知识是一致的；另一类是有关内容与学生的知识，这类知识不是数学家所具备的知识，而是教师在课堂中面对学生时，所具备的有效解释、评价和引导学生学习数学的知识。这类知识虽然与数学知识也有关，但主要是关于在课堂情境中传授数学知识的策略与方法的知识，集中体现在教学任务的设置中，如选择恰当的数学表征、分析学生的学习难点、评价学生的学习方法以及准备课程资料等。

对照这两种类型的知识，2004年希尔等人编制了小学数学中有关数的概念、运算、图形和函数等内容的测试题。为验证这些题目的效度和信度，希尔等人以加利福尼亚州数学教师培训项目的数据为基础，分析了这些测试题的内在结构和有效性。实证研究结论表明：(1)通过对量表中不同类型题目进行相关性分析后发现，内容知识和关于内容与学生的知识是两类不同的专业知识；(2)数学教学知识量表能够较准确地测量教师的数学教学内容知识，有很高的信度水平。该量表的编制对学科教学知识的实证研究发展产生了重要的推动作用^[7]。

一直以来，由于对学科教学知识的测量缺乏统一标准，研究者在研究学科教学知识与学生学业成绩的关系时，很难分辨出究竟是学科知识还是学科教学知识对学生学业成绩产生了影响。在舒尔曼看来，教师对学生的认识程度，以及积累起的帮助学生掌握正确概念的方法和经验，是学科教学知识的重要组成部分，这实际上是关于内容与学生的知识(knowledge of content and student，简称KCS)。为了更精确地测量KCS，2008年希尔等人专门开发了针对KCS的量表，并验证了其效度和信度^[8]。该量表较2004年的量表更加细化和深入。学科教学知识实证研究的关键是对其科学性的检测。从这个意义上来说，希尔等人多年来执著地推动学科教学知识的量化研究，尝试通过具体的量表把学科教学知识和学科知识精确地区别开，是深化学科教学知识研究所必需的，其针对学科教学知识测量所进行的研究工作具有奠基意义。

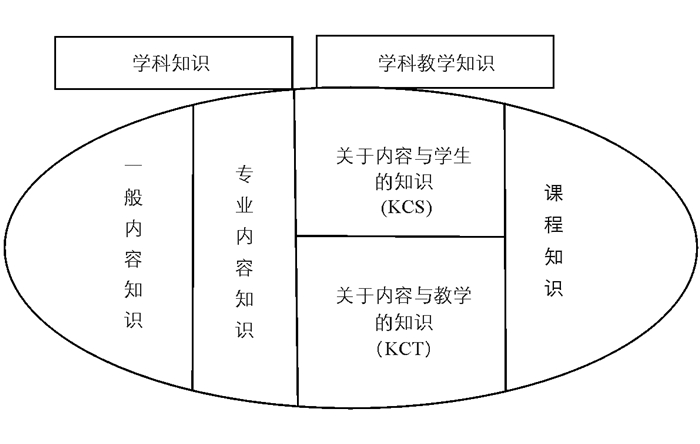
在上述对学科知识和学科教学知识测评的基础上，鲍尔等人在2008年发表的《教学所需的内容知识：什么使其专业化？》一文中提出了学科教学知识的分析框架，强调要解决教师掌握什么样的知识才能有效地开展教学工作的问题，必须坚持实践的观点，即要“自下而上”地追问教师在教学过程中必须要掌握哪些知识。鲍尔等人对舒尔曼的教师知识类型进行了新的分类，提出了教师知识结构的新分类框架^[6]，具体如图 2所示。

从图 2可以看出，学科知识分为一般内容知识和专业内容知识。前者是指最普通的知识，也是教师要掌握的基础知识；后者是指教师在教学过程中要具备的专业知识，这类知识是教师为了完成教学任务所应具备的学科知识。

从图 2还可以看出，学科教学知识分为关于内容与学生的知识和关于内容与教学的知识。前者是指那些可以把学科知识与学生知识相结合起来的知识。主要体现为：当选择一个例子时，教师要能预测到学生将从中发现哪些有趣的内容以及从哪些方面可以激发学生的学习动机；当确定一个教学任务时，教师要能预测到学生可能会如何完成，学生是觉得简单、容易还是复杂、困难。因此，教师必须能够清楚地捕捉到学生对学科知识不完全理解的方面。后者是指那些可以把学科知识与教学知识相结合起来的知识。学科中许多学习任务需要有与教学设计相对应的教学知识。主要体现为：当需要安排教学内容顺序时，教师要判断哪一个例子最先讲授，哪一个例子用来帮助学生理解更深奥的内容；当需要评价一个具体的教学主题时，教师要清楚地知道其表征方式在教学上的优劣；当开展课堂讨论时，教师要决定何时将学生进行分组，何时借用学生的评价展开观点，何时提出一个新问题或者新教学任务，以便引导学生进一步学习；等等。

鲍尔等人基于实证研究的成果，对学科教学知识进行了细致分类，试图通过对学科教学知识的测量，准确地分析出教师知识中哪些知识对学生的学业成绩产生了影响，哪些没有产生影响，这对学科教学知识的验证性研究具有重要意义。从现有的研究成果看，上述4类知识中，鲍尔率领的研究团队已经借助因素分析法和项目反应理论，对一般内容知识、专业内容知识以及关于学生和教学的课程知识是否能够独立存在，以及相互之间是否存在关联，都进行了深入研究。结果表明，这3类知识在教师知识结构中是独立存在的。鲍尔率领的研究团队已经开发出相对完整的测量量表，并且得到了广泛应用。

从理论上讲，教师学科教学知识的增长能提高学生的学业成绩，但这一假设是否真的成立，还需要有效的验证。希尔、罗恩(Brian Rowan)和鲍尔通过样本设计，最大程度地排除了其他变量如学校类型、学生家庭背景、教师学历和经验等影响因素的干扰，以考察教师学科教学知识与学生学业成绩之间的关系。他们对教师学科教学知识的测量沿用了希尔等人于2004年编制的量表。首先对取样教师的学科(数学)教学知识进行了测量，然后运用线性混合模式来估算学生变量、教师变量和学校特征对学生学业成绩的影响。研究的主要结论体现在3个方面：其一，教师的学科教学知识与教师的经验和职前准备没有显著的相关性；其二，通过统计分析发现，教师的学科教学知识是学生学业成绩的一个重要预测因素，其影响主要体现在教师学科教学知识每增加一个标准差，学生的学业成绩便会提高2.2个百分点，且教师的学科教学知识对学生学业成绩的影响要大于教师学历背景变量和教师每天平均教学时间对学生学业成绩的影响；其三，教师的学科教学知识对学生学业成绩的影响不是恒定的，具体而言，20%的数学教学知识水平较低的教师所教学生的数学成绩，可能与20%的数学教学知识水平较高的教师所教学生的数学成绩是相同的。这项研究力图通过对变量的控制来验证学科教学知识对学生学业成绩的影响。在所取样本中，学业成绩发生变化的学生中有6%或7%的人是由于受到了学校内部因素的影响。在学校内部因素变量中，数学课的时间、教师的准备和学历等都对学生的学业成绩没有产生独立的影响，但教师的数学教学知识对学生学业成绩的变化有直接影响。由此可见，教师的数学教学知识与学生学业成绩之间存在一定的相关性，或者教师的数学教学知识对学生学业成绩有一定影响，但至于两者之间是否存在因果关系，这项研究的数据尚不能得出结论^[9]。

从量化研究逻辑看，仅仅测量出学科教学知识是不够的，还要研究学科教学知识对学生学业成绩产生了怎样的影响以及如何产生影响等一系列问题。这使对变量的设计面临很大的挑战。这项研究通过对变量的控制和对统计方法的应用，分析出了学科教学知识对学生学业成绩的影响效应，在研究设计上有很大的贡献。

学科教学知识是通过课堂教学来影响学生学业成绩的，因此要揭示学科教学知识对学生学业成绩的影响机制，就需要探究学科教学知识对教学质量的影响。希尔等人于2008年开展了一项混合研究，对学科(数学)教学知识与教学质量之间的关系进行了细致研究。

这项研究指出，已有的关于学科(数学)教学知识的研究可以分为两类：一类是缺失性研究，就是研究教师缺少哪些学科教学知识以及其对教学的影响；另一类研究是丰富性研究，就是研究教师拥有哪些学科教学知识以及这些学科教学知识对教学有哪些影响。根据这两类研究，希尔等人提出了一个检验数学教学质量的基本框架。该框架分为6个指标：(1)数学错误；(2)对学生的不恰当对待；(3)把课堂教学实践与数学知识相结合；(4)数学的丰富性；(5)对学生的恰当应对；(6)数学语言。希尔等人应用数学教学知识测量量表和数学教学质量框架，选择参加数学教育工作坊的10位教师为研究对象，对这10位教师的数学教学知识和教学质量进行了测量。为便于比较研究，希尔等人按照数学教学知识和教学质量的得分情况，选择了其中的5位教师作为个案进行跟踪研究。这5位教师分为3种类型。第1类是一致型教师。就是数学教学知识与教学质量的变化是一致的，即：数学教学知识得分较高，数学教学质量也高；数学教学知识得分较低，数学教学质量也低。一致型教师有两位。第2类是不一致型教师。就是数学教学知识与教学质量的变化是反向的，即：数学教学知识得分较高，但教学质量较低；数学教学知识得分较低，但教学质量较高。不一致型教师也有两位。第3类是混合型教师。就是数学教学知识得分高，但教学质量处于中等水平的教师。混合型教师有一位。

基于这一设计，希尔等人收集了这5位教师的课堂视频进行质性分析，重点探讨了数学教学知识是如何影响课堂教学的，以及数学教学知识转化为课堂教学行为的阻碍因素等问题。通过对不一致型教师的分析，可以找出将数学教学知识转化为实际教学的阻碍因素。通过对一致型教师的分析，可以看出数学教学知识是如何转化为实际教学行为的。经过对个案的比较分析，可以准确地描述数学教学知识对课堂教学的影响机制^[10]。最终的质性分析结果表明，影响数学教学知识转化为教学质量的中介因素是：教师的数学教学方法、学生学习的兴趣和信念，以及教师对课程资料的掌握程度。

希尔等人的研究成果发表在国际顶尖期刊《认知与教学》上。这项研究的真正贡献不在于研究的结论，而在于其体现了一种独特的方法论意识——定量研究与质性研究的融合。目前，测量评价教学质量是教学研究中最为棘手的问题之一，由于教学活动有很大的不确定性，量化指标有时不一定能够客观地反映课堂教学的真实情况。希尔等人借助量化研究和质性研究两种方法，对学科教学知识与教学质量之间的关系进行了深入分析，弥合了定量研究与质性研究的分歧，在学科教学知识研究方法论上实现了重大突破，是混合研究的典型。

尽管研究显示学科教学知识是一种独立的知识，而且可以被较为精确地测量，但是这种知识能否通过培训获得以及其发展受哪些因素的影响等问题，还需进行实证研究才能得出可信的结论，这对教师教育政策的制定有直接影响。

希尔等人开展过两项关于教师学科教学知识影响因素的研究。其中，2004年的研究主要针对加利福尼亚小学数学教学培训项目。由于涉及的变量较多，研究运用了分层线性模型，主要探究了培训项目对提升教师学科教学知识是否有直接影响问题。数据分析结果表明：当培训能为教师提供参与数学分析、推理和交流的机会时，教师的学科教学知识会有显著提升，两者的相关系数为0.76；培训中的其他因素如教师学习动机、数学教学内容等对学科教学知识的影响不明显^[11]。

希尔等人于2007年开展的研究是通过测量初中教师的数学教学知识结构，分析了教师的数学教学知识与教师学历、教学经验和教学任务之间的关系。其相关性分析表明，初中教师的数学教学知识与其学历、接受的培训课程有直接关系。该项研究只是通过数据描述了数学教学知识的构成及其与教师自身变量之间的关系^[12]。

在舒尔曼提出教师知识分类理论30多年间，尽管针对不同的学科，出现了不同的学科教学知识分类框架，如格罗斯曼(Grossman)的英语学科教学知识^[13]、整合信息技术的学科教学知识^[14]等，但这些研究总体上依然没有摆脱舒尔曼的教师知识分类框架，只是针对具体学科内容进行了细化、重组和整合。真正体现研究深化的是由鲍尔、希尔等人领导的研究团队对学科教学知识所进行的一丝不苟的实证研究，这些研究使学科教学知识的研究摆脱了仅对新手教师与专家型教师进行简单的比较研究，以及对某类教师的案例研究等狭窄领域的束缚，构建了一个可验证和可解释的经验模型，这无疑是学科教学知识研究的一个重要转变，应该引起我们的关注。学科研学知识研究的现实意义主要体现在3个方面。

学科教学知识作为一个有学术生命力的概念，要真正指导实践，还必须通过切实可靠的验证。希尔等人之所以不厌其烦地追求对学科教学知识及其效果的精确界定和量化分析，就是要找到学科教学知识的内在结构及其对教学质量、学生学业成绩产生独立影响的证据。他们不盲目相信已有的有关学科教学知识的观点，即便一些已经被看作是常识的观点，如学科知识与学科教学知识是两类独立的知识、学科知识对学科教学知识有直接影响、学科教学知识水平高的教师教学质量高、学科教学知识水平高的教师对学生的学业成绩有直接影响等，而是力图通过可靠的证据，描述教师学科教学知识作为一种知识的内在结构对教学质量和学生学业成绩的影响，从而揭示学科教学知识发展的影响因素。这种证据本位的研究理念对深化学科教学知识研究具有重要的借鉴意义。

学科教学知识是教师在课堂情境中体现出的知识，具有情境性和默会性特征。如何揭示学科教学知识的独特要素和主要特征，成为其深化研究的关键性问题^[16]。在常规的研究中，通过个案的比较分析，可以揭示出学科教学知识的特征，但这些研究成果的普遍性常常受到质疑，无法在大规模的学科教学知识研究中应用。因此，要突破个案研究的局限，从量化研究的视角，探讨学科教学知识的一般特征以及对教学的影响等，就需要开发相应的研究工具，进行混合研究设计，以大规模的定量研究为主，辅以深度的个案分析，从而揭示学科教学知识发展的特征、过程和作用机制^[17]。研究设计上的这些突破，为准确认识学科教学知识结构及其发展路径提供了客观依据，提高了学科教学知识研究的学术质量。

学科教学知识的新研究以海量的数据、细致的统计方法、深入的案例研究为特点，客观地呈现了教师学科教学知识的现状以及学科教学知识对教学质量和学生学业成绩的影响，这对教师资格准入制度、教师培养政策的制定都具有重要意义。在我国教师资格认定中，研究者要逐步开发类似希尔等人开发的学科教学知识测量工具，对新入职教师的学科教学知识进行客观诊断，进而形成职前教师培养政策和内容框架^[18]。在职后教师培养过程中，相关单位要通过对经验型教师学科教学知识的精确测量，确定教师学科教学知识现状，制订有针对性的校本和区域教师培训方案，提高教师培养的针对性、科学性和实效性^[19]。

对学科教学知识的研究表明，教师专业发展的关键在于提高学科教学知识。希尔等人以准实验的研究方式，探讨了教师学科教学知识增长的有效路径，如采取探究、质疑、批判和互动等培训方式^[20]。学科教师知识的增长是教师基于课堂情境主动建构的过程，近年来学习科学的研究成果对教师专业发展提供了重要启示，应把学习的科学成果融入学科教学知识研究中，使教师成为主动学习者，并积极构建适合教师学科教学知识增长的学习环境和课程资源，这是未来教师专业发展的重要方向^[21]。

30多年来，国外学科教学知识的研究已积累了相当丰富的成果。在国内，李琼的研究系统探讨了学科知识与学科教学知识之间的关系，以及学科知识和学科教学知识对教学质量和学生学业成绩的影响^[22]。徐章韬的研究吸收了鲍尔等人的分析框架，选择个案的方式对师范生数学教学知识的发展路径进行了质性研究，但在研究方法上主要运用定性分析，而缺乏大规模的数据分析^[23]。未来，我国研究者要着重做好以下工作：吸收国外学科教学知识研究及职前职后教师培训的新成果^[24]；积极开展对我国教师学科教学知识的大样本测量；加强对我国教师学科教学知识现状的分析；更加精确地解释学科教学知识对教学质量和学生学业成绩的影响；逐步完善针对不同发展水平教师的学科教学知识增长培养路径；进一步推动学科教学知识研究成果的实践转化。