40年来经济高速增长所创造的奇迹，使得我国成为世界第二大经济体。按照世界银行(2014)划分标准，2010年我国人均GDP达4 382美元，已成功跨越贫困陷阱，正式跻身中等收入国家行列。截至2018年底，我国人均GDP达9 780美元，尚未达到12 736美元的高等收入界限。

但2010年以来，中国所面临的国内外环境发生重大变化，已由高速增长期进入增长速度换挡期，经济发展正在结构转型中迈向新常态，促进经济高速增长的传统动力机制逐渐弱化，经济发展面临着诸如人口老龄化、劳动力成本上升、投资效率降低、资源环境瓶颈等现实问题。深度转型期的中国面临着陷入“中等收入陷阱”的风险。

“中等收入陷阱”概念最早由世界银行于2006年在《东亚经济发展报告》中提出，表现为当一个国家(地区)的人均国民收入成功从低收入水平达到中等收入水平后，由于不能顺利实现经济发展方式的转变，或以往的发展路径难以保证总产出的持续增长时，导致经济增长动力不足，经济较长时期处于增速放缓甚至陷入停滞的一种稳定状态。这表明在经济发展的不同阶段，经济增长的动力机制是不同的，在低收入阶段能够有效促进经济增长的动力因素到中等收入阶段很可能失效。因此，能否在中等收入阶段转变经济增长方式，是一个国家能否成功跨越“中等收入陷阱”，跻身高等收入国家行列的关键。

国内外学者们围绕如何跨越“中等收入陷阱”进行了深入研究，其解决方案大致可以分为如下三类：一是缩小社会不公平，例如，Kuznets认为扭转收入分配不均的状况是中等收入阶段经济成功转型的关键^[1]，乔俊峰指出韩国采取的社会均等化政策为跨越“中等收入陷阱”提供了可靠保证，促进了高速增长和社会均等化发展^[2]；二是转变经济发展方式，例如，胡卫和高桂芳提出中国只有完成经济发展模式的转型，放弃原来依靠廉价劳动力的低成本出口导向战略，在产业结构、要素结构、内需结构等方面进行大刀阔斧的改革，才能进入高收入国家^[3]；三是提高科技创新能力，例如，Paus指出技术创新是中等收入国家向高收入国家迈进的驱动力^[4]，陈亮和陈霞认为我国应通过自主创新提高国际竞争力，以产业转移提升国际分工位置，为跨越“中等收入陷阱”提供更大的推力^[5]。当然，还有其他很多学者从金融发展规模、财政分权、市场化程度等视角对跨越“中等收入陷阱”提出了政策建议。

这些政策建议涉及范围很广，可见跨越“中等收入陷阱”是一项需从全方位因素去考虑的重大工程，但当前经济现实在体制、政策、技术诸方面都产生了经济结构调整和社会结构转型的极大掣肘，不消除这些因素，中国恐难跨越“中等收入陷阱”，保持经济的长期可持续增长。

本文的视角基于这样一个事实：资本积累在经济增长与发展过程中通过技术进步机制发挥着极其重要的作用。无论是物质资本积累所促进的生产要素效能提高，还是人力资本外溢性所引致的规模经济报酬递增，技术进步下资本存量的外部性程度对经济增长的作用越来越显著，从而影响到我国跨越“中等收入陷阱”的跃迁战略。

从外部性角度说明经济增长过程中技术进步的作用，经济增长理论已经有比较成熟的研究。Arrow就指出知识外溢来源于资本积累过程中的“干中学”，从而在经济外部性条件下，知识增长能够被资本积累增长指数化，生产函数表现出规模报酬递增^[6]。Romer将生产的收益递增视为知识外溢和资本积累所带来的正外部效应^[7]。Lucas则分析了人力资本对劳动生产率的递增收益，并指出资本的正外部效应还将引致他人资本及其他生产要素的收益递增，因而这种规模收益递增是长期经济增长的不竭之源^[8]。在实证研究方面，Grier最早构建了联合内生模型对拉丁美洲18个国家的相关数据分析表明，物质资本与人力资本两种生产要素之间存在互补性，即表现为正的外部性^[9]。胡永远利用我国1996-2000年省际区域数据进行GMM估计，分析出我国物质资本与人力资本之间也存在显著的双向关系，从而共同推动经济的持续增长^[10]。张小雪等构建了要素积累外部性与可持续增长的理论模型，指出人力资本与物质资本的非均衡导致了物质资本积累的正外部性显著下降，从而影响我国实际GDP增长放缓^[11]。

上述对资本外部性的研究，都把资本要素作为知识积累的外生变量，阐述了物质资本和人力资本作为生产要素在生产过程中对经济增长的促进作用。事实上，生产者通过在生产过程中不断地学习知识和积累经验，从而使其被资本积累指数化，成为一个内生变量。同时，在经济外部性的条件下，单个生产者的知识增长还将引致整个社会普遍受益。正是这种源于经济系统内部的技术进步机制及其外溢效应，使得产出表现为递增收益，经济增长才得以持续，顺利推动我国跨越“中等收入陷阱”。

出于这种观察，本文试图基于资本外部性程度的视角，深入研究技术进步机制中资本积累与外溢效应对我国经济增长及跨越“中等收入陷阱”的内在作用机理。我们也利用1978-2018年时间序列数据构建ARIMA模型，对我国人均国内生产总值和资本正外部性程度进行预测分析，以估算出我国跨越“中等收入陷阱”的时间维度。

首先考虑一个标准的索洛模型。假设经济表现为规模报酬不变的总量生产函数，即，Y=AK^αL^1-α，0＜α＜1，其中Y、A、K、L分别表示总量上的产出、技术进步水平、资本存量和劳动力。记y=Y/L，k=K/L分别为人均产出和人均资本存量，则总量生产函数的集约式表示为y=f(k)=AK^α，0＜α＜1。

资本积累方程为：

其中储蓄率s和折旧率δ均外生给定。假定人口增长率也外生给定，即$\dot{L} / L=n>0 $。把该式以集约形式表达：

此即标准索洛模型的核心方向。现在引入内生技术进步。内生技术进步表现为标准的干中学方式，即假设技术进步内生依赖于社会平均资本存量，A=f(k)=A₀k^γ，A₀＞0，其中，γ>0代表资本存量投入的外部性程度。该技术进步函数表明，社会平均资本积累水平越高，则技术水平越高。

因此，公式(2)变成：

当$ \dot{k}=0$时，得到稳态：

其中k^*为稳态人均资本存量水平。稳态的稳定性取决于下列条件：

可见，若α+γ＜1时，即资本收入份额与资本存量外部性程度之和小于1时，(5)式为负，稳态是稳定的。

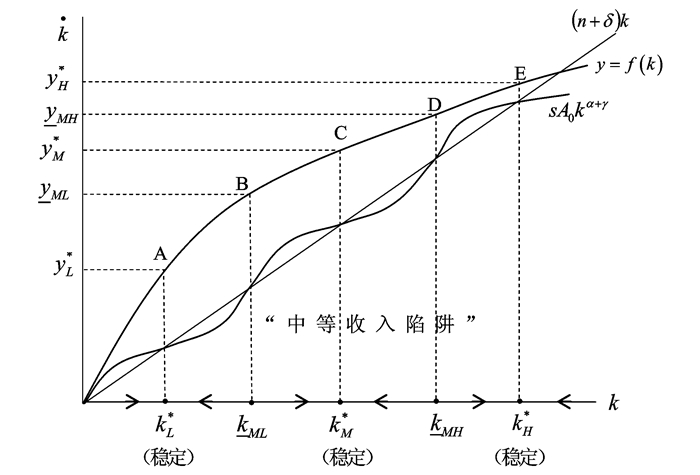
按照通常的定义，我们可以把“中等收入陷阱”理解为一个有着中等水平人均资本存量和人均产出的稳定状态，“陷阱”是指这种稳态是稳定的，即一旦偏离这一稳态，经济有着回复到该稳态的趋向。根据本文上述动力模型，可以得到图 1^①。

① 对函数sA₀k^α+γ=h(k)，h′=(α+γ)sA₀k^α+γ-1＞0决定其图形始终正斜率，但h″=(α+γ-1)(α+γ)sA₀k^α+γ-2不确定，当时α+γ＜1时h″＜0，α+γ＞1时h″＞0。假设存在这种相互交替变化的情形。

图 1考虑了动态经济系统(3)存在多重均衡的情形，其中，分别对应于低、中、高收入的人均资本积累水平k_L^*、k_M^*和k_H^*都是具有稳定性质的稳态，而不稳定的稳态水平k_ML和k_MH代表某种门槛值，一旦达到这一门槛值，经济便趋于停留在这些稳态。例如，当资本积累处于k＜k_ML时，经济无法起飞而落入低收入陷阱之中，当资本积累处于k_ML＜k＜k_MH时，经济会陷入“中等收入陷阱”，只有资本积累k＞k_MH时，才能突破“中等收入陷阱”，而向高收入均衡运动。

可见，在一个经济体的平均资本积累由中等水平向高等水平运动的过程中，存在着一个中高水平的门槛(k_MH)。跨越这一门槛，经济体系将趋于高收入水平；反之，经济体会一直徘徊在中等收入水平，即落入“中等收入陷阱”区间(k_ML，k_MH)。

经济增长过程中会出现这种情况吗？模型的关键在于动力系统(3)的非凸性质。可以这样理解，低水平发展阶段经济主要依赖于报酬递减盛行的传统农业，而现代工业的崛起会使得经济更多地呈现报酬递增，而随着机器大生产的好处被耗尽，经济重归报酬递减^[12]。如果经济找到新的发展动力，例如改革开放，或网络等新经济，或结构调整，规模报酬递增就可能再度居支配地位。如此反复，就导致了经济发展中的起飞、停滞与跃迁。

下面基于中国经济1978-2018年时间序列数据，运用软件Eviews 8.0构建ARIMA(p, d, q)模型，对我国人均国内生产总值进行预测分析，以估算出在经济发展新常态背景下，我国跨越“中等收入陷阱”的时间维度。具体方法如下：首先，对样本时间序列进行平稳性检验，以保证数据的平稳性；然后，运用AIC信息准则、SC施瓦茨准则及Q统计量方法，识别与检验最优模型；最后，对最优模型进行参数估计，并对样本数据进行预测与分析。

以时间序列理论为基础，本文选取改革开放以来1978-2018年我国支出法核算人均国内生产总值(PGDP)为基础数据资料，并用1978年不变价的国内生产总值指数剔除物价因素，数据均来自《中国统计年鉴》。

ARIMA(p, d, q)模型即单整自回归移动平均模型，是美国统计学家G.E.P.Box和G.M.Jenkins(1976)首次提出，广泛运用于时间数据分析的一种预测精度相当高的短期预测方法。但ARIMA模型只适用于平稳的时间序列，因此为了保证时间序列的平稳性，需要对样本数据进行平稳性检验。

首先，消除数据的异方差性，对样本数据进行对数化处理，设定Ln(PGDP)表示人均国内生产总值。通过描绘原始时间序列图看出，我国原始Ln(PGDP)呈现出明显的上升趋势，不具有周期变化和季节波动，即是非平稳的。同时，观察相关图和偏相关图也得到同样的结论，Ln(PGDP)的相关图衰减得很慢，说明原始序列非平稳。

为消除原始数据的趋势性，选择用差分的方法对样本数据进行平稳化处理。对原始序列进行一、二阶差分，设定DY是Ln(PGDP)的一阶差分序列，DZ是Ln(PGDP)的二阶差分序列。

经过差分处理，从表 1单位根检验结果可以看出，二阶差分序列在1%、5%、10%的显著性水平下均拒绝原假设，接受不存在单位根的结论，则认为二阶差分后序列平稳。因此，可确定Ln(PGDP)序列是2阶单整序列，即Ln(PGDP)~I(2)。

获得平稳时间序列后，ARMA(p, q)模型的识别与定阶则可通过采用AIC信息准则和SC施瓦茨准则来确定。通过比较发现，ARMA(1, 3)模型的AIC和SC值均较小，因此选取ARMA(1, 3)模型进行下一步检验。

为进一步确定最优模型的参数，对ARMA(1, 3)模型进行显著性和白噪声检验。通常采用Box Pierce(1970)提出的Q统计量方法来完成模型残差序列的白噪声过程检验。检验结果表明，ARMA(1, 3)模型的Q值小于对应自由度卡方分布的检验值，且Prob列读出拒绝原假设的概率较大，即残差序列为白噪声序列，故选择ARMA(1, 3)模型为最终模型。

使用软件Eviews 8.0对ARMA(1, 2, 3)模型的OLS估计结果如下：

并运用上述ARMA(1, 2, 3)模型，对我国2019-2025年人均GDP进行预测，预测结果如下表 2所示。

按照世界银行2014年标准，人均GDP低于1045美元为低收入国家，在1 045~4 125美元间为中等偏下收入国家，4 126~12 735美元之间的国家被归类为中等偏上收入国家，高于12 736美元为高收入国家。

参照于此，我们可以从经验上定义一些门槛值。例如，进入中等收入水平国家行列的最低人均收入门槛值为y_ML=1 045美元，进入高收入水平国家行列的最低人均收入门槛值为y_MH=12 735美元。

2018年我国人均GDP达9 780美元，因此可以判定目前我国经济处于图 1中CD段(中高收入阶段)，人均GDP趋向回复到稳态C。只有超过门槛值D点即y_MH，人均GDP才将向稳态E点运动，达到高等收入水平。我们的模型预测表明，2022年我国人均GDP将超过门槛值y_MH，也就是我国会成功跨越“中等收入陷阱”。

这一预测分析结果也得到了其他学者的印证。例如郑秉文认为，在其他条件不变情况下，按照目前的增长速度推测，我国大约在“十四五规划”期间实现“第三次跨越”，顺利进入高收入组国家^[13]。胡鞍钢、周绍杰假定中国人均GDP实际年平均增长率为7%，不考虑人民币升值情况下，中国将在2022-2023年达到高收入水平门槛，从人口比例上看，到2020年有2/5左右人口达到高收入水平，到2025年有2/3以上人口达到高收入水平^[14]。世界银行(2012)在《2030年的中国》研究报告中指出，中国经济在经历了30多年后的高速增长后，潜在增长率很大可能转入中速增长阶段，但如果中国经济仍能以6%~7%的增长速度持续增长10~20年，将会成功进入高收入社会^[15]。

根据前面第二部分的理论模型，可以得到经济的稳态人均产出水平为：

进而可以推断资本存量投入外部性：

我们需要估算出一个资本积累外溢效应水平，它能够使得经济达到高收入水平最低门槛值即y_MH=12 735美元。这意味着我们也需要知道经济体的其他基本参数，包括技术参数A₀，社会储蓄率s，人口增长率n，折旧率δ，以及资本收入份额α。通常使用校准法得到这些参数值：

技术参数A₀。该值代表均衡技术水平，只有水平效应，没有波动效应，故通常取值A₀=1。

储蓄率s。根据国民收入核算公式Y=C+S，故国内总储蓄等于支出法核算的国内生产总值减去最终消费支出，储蓄率即为国内总储蓄与国内生产总值的比值。我们取储蓄率为过去10年(2009-2018年)的平均值，即s=0.487 3。

人口增长率n。取值为过去10年人口自然增长率的平均值，即n=0.004 9。

折旧率δ。国际上认为季度折旧率一般取值为0.025，年度折旧率为0.1，本文假设我国固定资产使用年限平均为10年，故δ=0.1。

资本收入份额α。通过对总量生产函数加以估计，参考文献中的通常做法，令α=0.46。

因此，在给定这些参数值的条件下，计算出突破“中等收入陷阱”的资本外溢程度为γ=0.400 2。该值是一个理论值。

目前，我国已经进入中高收入国家行列，2018年人均GDP达9 780美元，再结合当年实际的国民储蓄率、人口增长率与资本收入份额，可以估算出2018年资本外溢程度为γ=0.332 5。可见，它离上述理论值还有一段差距。

要根据公式(8)估算经济中资本存量外部性，需要知道稳态人均产出y^*。按照宏观经济学基本原理，它是使得经济中储蓄投资平衡的产出。我们在《中国统计年鉴》支出法GDP核算中，按照最终储蓄率估计出总储蓄，假设它全部转化为投资，使用这一数据替换掉原来支出法里的资本形成总额，就可以得到一个均衡产出序列。在此基础上来估计经济中的资本存量外部性。其变动情况如图 2所示。

可以看出，1978-2018年能够实现稳态产出的资本存量外部性呈不断波动的上升趋势。2000年时资本存量正外部性程度达到最大值0.388 4，随后小幅下降，直到2009年开始回升，根据变化趋势判断，资本存量正外部性程度依然会继续增大，这似乎与我国人均实际国内生产总值的变动特征趋同。按照世界银行划分标准，2001年我国人均GDP达1 053美元，实现从低收入国家过渡到中等偏下收入国家，但并未完全跨越“贫困陷阱”。随后在2010年，人均GDP突破4 126美元，顺利跻身中等偏上收入国家行列，正逐步向高等收入国家进阶。这是一种巧合？还是说资本存量正外部性与人均国内生产总值之间有着密切的关系？

学者们的研究表明，内生技术进步下的资本存量正外部性确实对人均GDP的增长有着显著的影响。阿罗^[6]通过“干中学”模型对技术进步内生化作了最初的尝试，他认为技术进步是资本积累的副产品，并且知识积累或资本积累具有外部性，提高一个厂商的资本存量会导致其知识存量以及生产率相应增加，其他厂商也可通过积累经验提高生产率，从而整个社会的生产函数具有报酬递增。罗默^[7]指出内生技术进步的来源之一就是经济外部性，主要体现在知识外溢和人力资本积累的外在效应上，而后者对技术进步的正外部效应则更加显著。他借用马歇尔“外部经济效应”的概念，认为生产者在生产物质资本时，经验的增长被资本积累的增长指数化，从而在经济正外部性条件下，促使整个社会普遍受益，即出现了知识外溢。卢卡斯^[8]把人力资本从物质资本中分离出来，分析了人力资本对自身劳动生产率的递增收益，并指出这种正外部效应还将引致他人生产要素收益递增，这样经济增长机制才得以持续。

前述理论分析表明，技术进步内生依赖于资本存量，无论是物质资本积累所促进的生产要素效能提高，还是人力资本外溢性所引致的规模经济报酬递增，技术进步下资本存量的正外部性对经济增长的作用越来越显著。那么其应保持如何的增长水平才能促进我国成功跨越“中等收入陷阱”，顺利跻身高等收入国家呢？

对资本存量投入外部性程度进行估算得到，“十三五”时期我国年平均资本存量投入外部性程度为0.399 4，“十四五”时期增长到0.401 7。可见，要保证我国经济规模报酬持续递增，并在“十四五”时期顺利跨越“中等收入陷阱”，资本存量需要通过技术进步机制发挥更大的正经济外部效应。

本文基于我国经济发展新常态下资本要素积累对产出的显著影响，通过技术进步机制中物质资本积累或人力资本投资的外溢效应，解释了我国经济持续增长以及跨越“中等收入陷阱”的内在作用机理。并利用1978-2018年时间序列数据构建ARIMA模型，对我国人均国内生产总值和资本正外部性程度进行预测分析，以估算出我国跨越“中等收入陷阱”的时间维度，得到以下结论：

第一，中等水平的资本存量以及由其所决定的中等收入水平是稳定的“稳态”，即“中等收入陷阱”是一个有着中等水平人均资本存量和人均产出的稳定状态。要想打破这种均衡的状态，人均GDP必须超过中等偏上收入水平的节点，才将收敛于高收入水平方向运动，否则将陷入“中等收入陷阱”。

第二，技术进步机制下，随着“干中学”中物质资本积累以及人力资本投资的溢出效应，我国资本存量投入始终表现为经济正外部性，并且对经济增长的作用不断显著。根据变动趋势判断，为保证产出规模报酬持续递增，物质资本和人力资本需要通过技术进步机制发挥更大的正经济外部效应。

第三，根据模型估算结果，2018年我国人均GDP为9 780美元，再用5年时间，我国人均GDP将在2022年成功跨越“中等收入陷阱”。但考虑到目前国际市场汇率波动较大，且近年来人民币贬值，故有可能推迟我国跨越“中等收入陷阱”的时间维度。

基于本文研究结果，结合当前我国经济发展进入新常态的事实，对我国跨越“中等收入陷阱”提出如下政策建议：首先，加快经济社会结构转型，推动经济发展由“要素驱动”向“创新驱动”转变，提高自主创新能力，为经济的可持续性发展提供新的动力机制；其次，加大物质资本和人力资本投资，特别强调人力资本积累的外溢效应，鼓励技术创新，实施创新人才发展战略，提升以知识为导向的经济增长质量与效益。同时，还要兼顾社会公平问题，在推动我国新型城镇化建设稳步向前发展的过程中，坚持城乡一体、协调发展、互惠互利、共同富裕的原则，进一步缩小城乡收入差距，实现城乡统筹协调发展。