-
文献[1]的第ⅩⅤⅠⅠ章引入了复形的投射和内射分解的概念,该分解现在被定义为Cartan-Eilenberg分解,简记为CE-分解.文献[2]引入了CE-内射分解与CE-投射分解的概念,并考虑了复形的CE-内射分解和CE-投射分解的存在性.文献[3]讨论了CE-投射、CE-内射和平坦复形及其CE-分解的存在性,并证明了每个复形有CE-内射包络和CE-平坦覆盖.设
$ \mathscr{A} $ 是一个Abelian范畴,$ \mathscr{C} $ 是$ \mathscr{A} $ 的一个加法满子范畴.文献[4]提供了如何由短正合列中两项(余)真$ \mathscr{C} $ -分解的存在性得到第三项(余)真$ \mathscr{C} $ -分解的存在性的方法.受以上工作的启发,本文研究了关于满子范畴$ \mathscr{C} $ 的CE-(余)真分解的存在性及构造.本文中,
$ \mathscr{A} $ 是一个Abelian范畴,并且$ \mathscr{C} $ 是$ \mathscr{A} $ 的加法满子范畴.其它未定义的术语参见文献[5].定义1[3] 如果以下序列是正合的:
(ⅰ)
$ 0 \longrightarrow {C_0} \longrightarrow {C_1} \longrightarrow {C_2} \longrightarrow 0 $ ;(ⅱ)
$ 0 \longrightarrow Z\left( {{C_0}} \right) \longrightarrow Z\left( {{C_1}} \right) \longrightarrow Z\left( {{C_2}} \right) \longrightarrow 0 $ ;(ⅲ)
$ 0 \longrightarrow B\left( {{C_0}} \right) \longrightarrow B\left( {{C_1}} \right) \longrightarrow B\left( {{C_2}} \right) \longrightarrow 0 $ ;(ⅳ)
$ 0 \longrightarrow {C_0}/Z\left( {{C_0}} \right) \longrightarrow {C_1}/Z\left( {{C_1}} \right) \longrightarrow {C_2}/Z\left( {{C_2}} \right) \longrightarrow 0 $ ;(ⅴ)
$ 0 \longrightarrow {C_0}/B\left( {{C_0}} \right) \longrightarrow {C_1}/B\left( {{C_1}} \right) \longrightarrow {C_2}/B\left( {{C_2}} \right) \longrightarrow 0 $ ;(ⅵ)
$ 0 \longrightarrow H\left( {{C_0}} \right) \longrightarrow H\left( {{C_1}} \right) \longrightarrow H\left( {{C_2}} \right) \longrightarrow 0 $ ;则称复形序列
$ 0 \longrightarrow {C_0} \longrightarrow {C_1} \longrightarrow {C_2} \longrightarrow 0 $ 是CE-正合的.注1 由文献[3]可知,在定义1的序列中,若(ⅰ)与(ⅰⅰ)或(ⅰ)与(ⅴ)正合,则(ⅰ)-(ⅴⅰ)都正合.
定义2 设M∈
$ \mathscr{A} $ ,称CE-正合列(长度有限或无限)为M的CE-
$ \mathscr{C} $ -分解,其中Ci∈$ \mathscr{C} $ .定义3 如果定义2中的CE-正合列是M的
$ \mathscr{C} $ -分解,且为Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,则称该正合列为M的真CE-$ \mathscr{C} $ -分解.对偶地有M的CE-
$ \mathscr{C} $ -余分解与M的余真CE-$ \mathscr{C} $ -余分解的定义.定理1 设
是
$ \mathscr{A} $ 中的CE-正合列.令是X0的一个CE-
$ \mathscr{C} $ -分解,且是X1的一个真CE-
$ \mathscr{C} $ -分解.则:(ⅰ)有以下两个CE-正合列:
(ⅱ)如果CE-正合列(2)与(3)是Hom
$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,则序列(4) 是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的;(ⅲ)如果CE-正合列(2) 是Hom
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,则序列(4) 是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的;(ⅳ)如果CE-正合列(1) 是Hom
$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合(Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合)的,则序列(5) 是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合(Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合)的.证 (ⅰ)对i≥1,令:
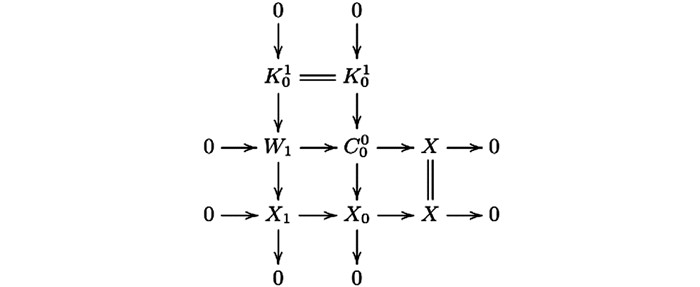
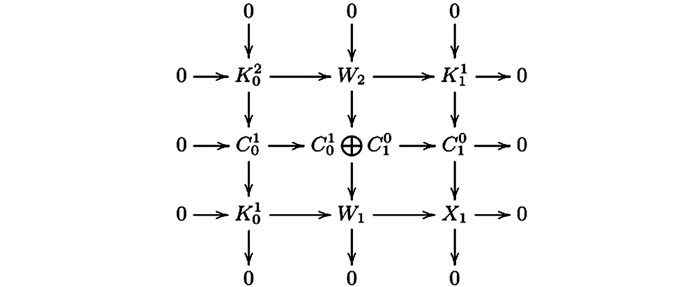
考虑拉回图 1.
图 1的第三列是Hom
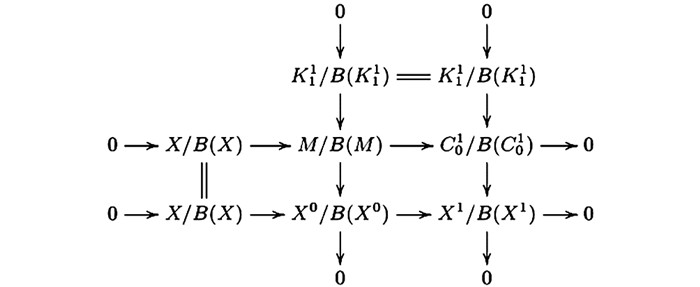
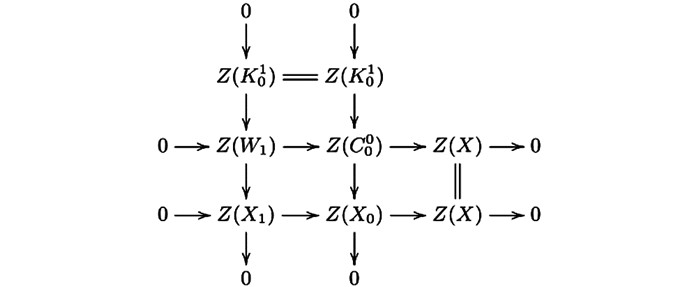
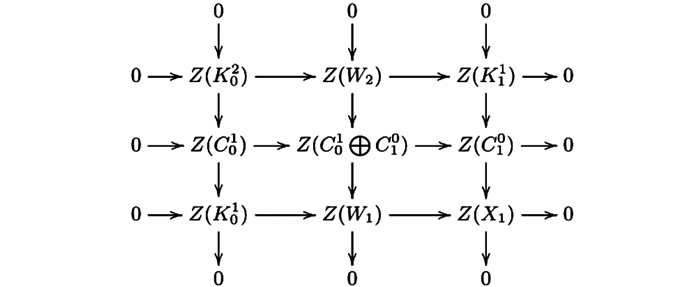
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,所以由文献[4]的引理2. 4(1) 知,第二列是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的.根据图 1可得交换图 2.因为图 1中的第三行及第三列是CE-正合的,所以图 2的第三行与第三列是正合的.因为—/B(—)是右正合-函子,所以第二行与第二列是左正合的.因此图 1的第二行与第二列是CE-正合的.再由文献[4]的3.1(1),我们有行与列正合的交换图 3.其中
因为图 3中第二行与第三行是Hom
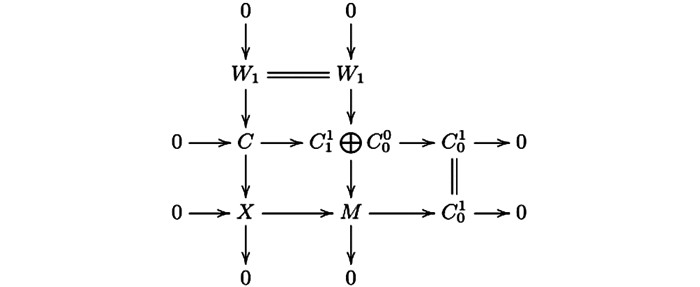
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,所以第一行是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的.根据图 3,我们可以得交换图 4.因为图 4的第一列与第三列是正合的,根据蛇引理可得第一行与第二列是正合的.因此图 3的第一行与第二列是CE-正合的.我们有拉回图 5,则可得交换图 6.
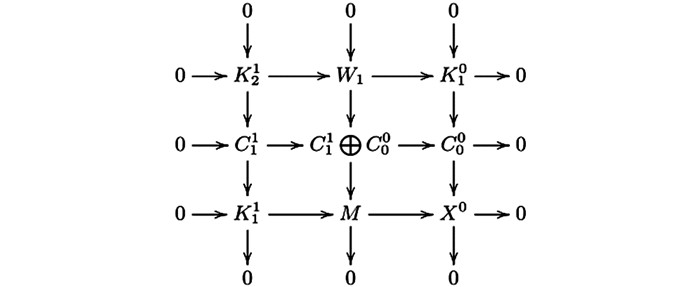
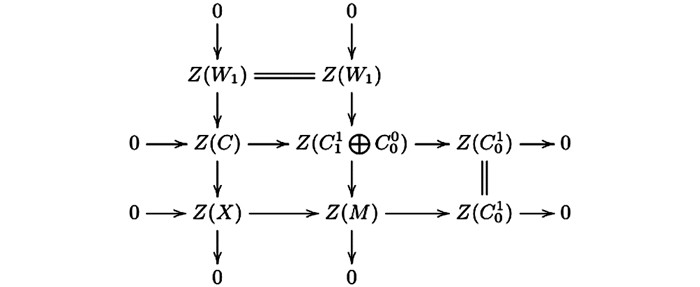
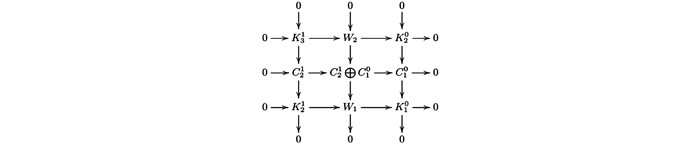
因为交换图 6的第二行是正合的,由蛇引理可知第一列是正合的,因此图 5的第二行与第一列是CE-正合的.再由文献[4]的3.1(1),我们有以下行与列正合的交换图 7,其中
$ {W_2} = {\rm{Ker}}\left( {C_2^1 \oplus C_1^0 \longrightarrow {W_1}} \right) $ ,且图 7中第一行是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的.根据以上证明可得图 7的第一行与第二列是CE -正合的.重复以上过程可得序列(4) 与(5) 是CE-正合的.(ⅱ)因为CE-正合列(2) 与(3) 是Hom
$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,所以在图 3中第一列与第三列是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,由文献[4]的2.5(1) 知,第二列是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的.因此图 5的第一列是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,且图 7的第二列是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的.故序列(4) 是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的.(ⅲ)因为CE-正合列(2) 与(3) 是Hom
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,所以在图 3中第一列与第三列是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的.由(ⅰⅰ)的证明可得到Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合列:因此可得序列(4)是Hom
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的.(ⅳ)如果CE-正合列(1) 是Hom
$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,则图 1中第二行是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,且图 5中第二行是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的.故序列(5) 是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的.如果CE-正合列(1) 是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,由文献[4]的引理2. 4(1) 知,图 1中第二行是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,且图 5中第二行是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的.故序列(5) 是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的.对偶于定理1,我们有如下定理:
定理2 设
是
$ \mathscr{A} $ 中的CE-正合列.令是Y0的一个CE-
$ \mathscr{C} $ -余分解,且是Y1的一个余真CE-
$ \mathscr{C} $ -余分解.则:(ⅰ)有以下两个CE-正合列:
(ⅱ)如果CE-正合列(7) 与(8) 是Hom
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,则序列(9) 是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的;(ⅲ)如果CE-正合列(7) 是Hom
$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,则序列(9) 是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的;(ⅳ)如果CE-正合列(6) 是Hom
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合(Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合)的,则序列(10) 是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合(Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合)的.定理3 设
是
$ \mathscr{A} $ 中的CE-正合列.令是X0的一个真CE-
$ \mathscr{C} $ -分解,且是X1的一个CE-
$ \mathscr{C} $ -分解.则:(ⅰ)有CE-正合列
(ⅱ)如果CE-正合列(11)-(13) 是Hom
$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,则序列(14) 是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的;(ⅲ)如果CE-正合列(11) 与(13) 是Hom
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,则序列(14) 是Hom$ \mathscr{A} $ $ \mathscr{C} $ ,—)-正合的.证 (ⅰ)对1≤i≤n-j(j=0,1),令
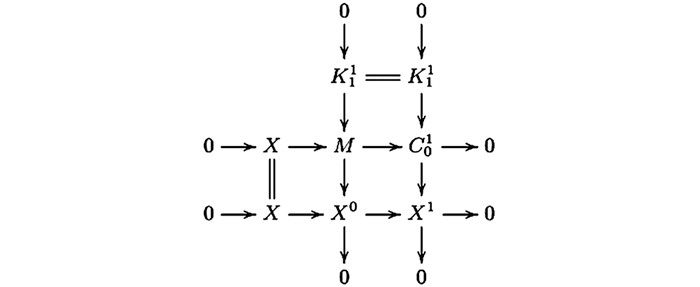
$ K_j^i = {\mathop{\rm Im}\nolimits} \left( {C_j^i \longrightarrow C_j^{i - 1}} \right) $ .考虑拉回图 8.因为图 8中第二列是Hom
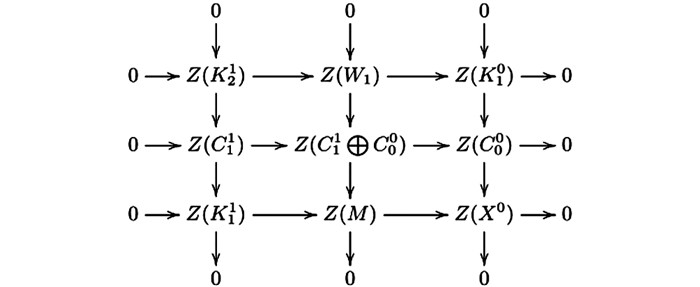
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,所以由文献[4]的引理2.4(1) 知,第一列是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的.我们有交换图 9.因为图 8中的第三行与第二列是CE-正合的,所以图 9的第三行与第二列是正合的.因为交换图 9的第二行是正合的,再由蛇引理可得第一列是正合的.则图 8的第二行与第一列是CE-正合的.由文献[4]的引理3. 1(1) 知,有如下行与列正合的交换图 10,其中
$ {W_2} = {\rm{Ker}}\left( {C_0^1 \oplus C_1^0 \longrightarrow {W_1}} \right) $ .因为图 10的第二行与第三行是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,所以由文献[4]的引理3.1(1) 得第一行是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,其中:由蛇引理可得图 11中第一行与第二列是CE-正合的.因此序列(14) 是CE-正合的.
(ⅱ)因为图 8的第三行与第二列是Hom
$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,由文献[4]的2.5(1) 知,图 8的第二行是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的.再由图 10的第一列与第三列是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,可证图 10的第二列是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的.因此序列(14) 是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的.(ⅲ)因为图 8的第三行与图 10的第三列是Hom
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,所以由文献[4]的引理2.5(2) 可证图 8中第二行与图 10中第二列是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的.因此序列(14) 是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的.对偶于定理3,我们有如下定理:
定理4 设
是
$ \mathscr{A} $ 中的CE-正合列.令是Y0的一个余真CE-
$ \mathscr{C} $ -余分解,且是Y1的一个CE-
$ \mathscr{C} $ -余分解.则:(ⅰ)有CE-正合列
(ⅱ)如果CE-正合列(15)-(17) 是Hom
$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的,则序列(18) 是Hom$ \mathscr{A} $ ($ \mathscr{C} $ ,—)-正合的;(ⅲ)如果CE-正合列(15) 与(17) 是Hom
$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的,则序列(18) 是Hom$ \mathscr{A} $ (—,$ \mathscr{C} $ )-正合的.
Cartan Eilenberg-(Co) Proper Resolutions
-
摘要: 设$ \mathscr{A} $是一个Abelian范畴.定义了Cartan Eilenberg(余)真分解(简称为CE-(余)真分解),给出了短正合列中CE-(余)真分解的构造及与函子Hom$ \mathscr{A} $(——,-)的关系.Abstract: Let $ \mathscr{A} $ be an Abelian category. This paper defines the Cartan Eilenberg-(co) proper resolution (referred to as CE-(co) proper resolution), provides a method to construct a CE-(co) proper resolution in a short exact sequence, and gives some relationship between it and the functor Hom$ \mathscr{A} $(——, -).
-
Key words:
- CE-(co) proper resolution /
- exact /
- CE-exact sequence .
-

-
图 2 关于图 1的-/B(—)函子
图 4 关于图 3的循环的函子
图 6 关于图 5的循环的函子
图 9 关于图 8的循环函子
图 11 有关图 10的循环函子
-
[1] CARTAN H, EILENBERG S. Homological Algebra [M]. State of New Jersey: Princeton University Press, 1956: 362-376. [2] doi: https://webusers.imj-prg.fr/~georges.maltsiniotis/jlv.html VERDIER J L. Des Catégories Dérivées Des Catégories Abéliennes [J]. Astérisque, 1996, 239: 227-229. [3] ENOCHS E E. Cartan-Eilenberg Complexes and Resolution [J]. J Algebra, 2011, 342(1): 16-39. doi: 10.1016/j.jalgebra.2011.05.011 [4] doi: http://maths.nju.edu.cn/~huangzy/papers/Journal%20of%20Algebra/progor.pdf HUANG Z Y. Proper Resolutions and Gorenstein Categories [J]. J Algebra, 2012, 393(11): 142-169. [5] 陈文静, 杨晓燕.强和强泛Gorenstein FP-内射模[J].西南大学学报(自然科学版), 2014, 36(8): 75-78. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-XNND201408012.htm -



 下载:
下载: