-
反应扩散方程的边界控制问题有广泛的工程背景.在对一维的反应扩散方程的边界控制的研究中,最早考虑在容器的一端加控制的情况[1-2].当区间的一端移动时,在移动端加控制的情况已被解决[3-4].并且对输入时滞系统的边界控制的研究也取得成功[5].对高维系统的边界控制的研究,现在只解决了矩形区域和立方体区域[6],以及圆形区域上温度的边界控制[7].在其它高维区域上的反应扩散方程的边界控制问题尚无很好的结果.因此本文首先考虑曲边矩形上的系统的边界控制,即系统
其中:a,λ>0;φ(x)在[0,l]上可微;P={(x,y)|0<x<l,0<y<φ(x)};u(x,y,t)为温度;U(x,t)为边界控制输入.随后考虑曲顶柱体上的系统
其中:a,λ>0;Ω⊂ℝ2是有界开域;V={(x,y,z)|(x,y)∈Ω,z∈(0,f(x,y))};D是Ω的边界;f(x,y)在Ω上连续;u(x,y,z,t)为温度;U(x,y,t)为边界控制输入.
本文利用反步控制(Backstepping)方法,先给出一个指数稳定的目标系统,找到边界控制将原系统转化为目标系统.随后用李雅普诺夫方法证明目标系统是指数稳定的,并证明在所给出的边界控制下闭环系统稳定.
全文HTML
-
考虑系统(1)-(3) 的控制设计.引入变换
边界控制为
-
将(8) 式两边同时对t求导,再分别同时对x,y求二阶偏导数并化简,可得
取核函数满足
得到
此时(8) 式将系统(1)-(3) 转化成目标系统
文献[2]中已给出方程(10)-(12) 的解为
-
定理1 当a>0时,系统(13)-(14) 指数稳定.即存在常数M,N>0,使得
其中
-
设(8) 式的逆变换为
类似k(y,z)的求解过程,可解得
在边界控制(9) 下,系统(1)-(3) 指数稳定.
1.1. 控制器设计
1.2. 目标系统的指数稳定性
1.3. 逆变换及稳定性
-
考虑系统(4)-(7) 的控制设计,引入变换
边界控制为
-
变换(15) 两边分别对x,y,z求二阶偏导数,对t求偏导数,并化简,可取核函数满足:
得到
此时(15) 式将系统(4)-(7) 转换成目标系统
其中Γ为V的边界.
方程(16)-(18) 的解为
-
定理2 目标系统(19)-(20) 指数稳定,其中
-
记(15) 式的逆变换为
可知
下证系统(4)-(7) 指数稳定.
对(21) 式两边求范数,得
由施瓦茨不等式可知
由于对任意(x,y)∈Ω∪D,q(z,s)在{(z,s)|z∈(0,f(x,y)),s∈(0,z)}上有界,故存在连续且在Ω∪D上有界的函数K(x,y),满足
从而有
由此可得
由于K(x,y),f(x,y)在Ω上有界,存在常数C>0,满足
从而
于是,存在常数C1>0,使得
类似可证明存在常数C2>0,使得
从而有
故u(x,y,z,t)指数稳定.
2.1. 控制器设计
2.2. 目标系统的指数稳定性
2.3. 逆变换及稳定性
-
考虑如下系统
其中
当
时,原系统变为
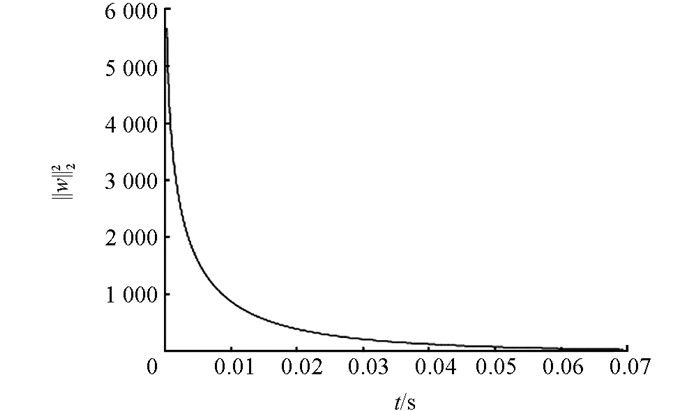
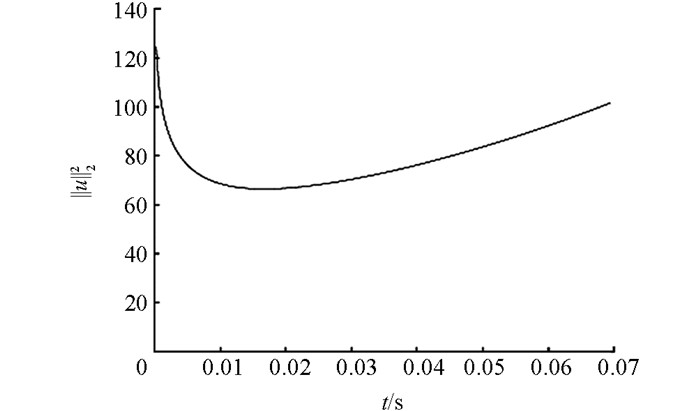
其中w(x,y,0)≠u(x,y,0).此时‖u‖22和‖w‖22与时间t的关系分别如下图所示:
-
本文主要研究了曲边矩形及曲顶柱体上温度的边界控制.应用原有的反步控制方法,根据相应条件导出核方程,进而得到核方程的解和控制律,并证明闭环系统是指数稳定的.为了更好证明理论正确性,对二维系统进行数据仿真,实验结果与理论推导相吻合.与已有的成果相比,由于所施加控制的一端的形状对控制律没有影响,因此本文扩展了原有的Backstepping方法的适用范围.



 下载:
下载: