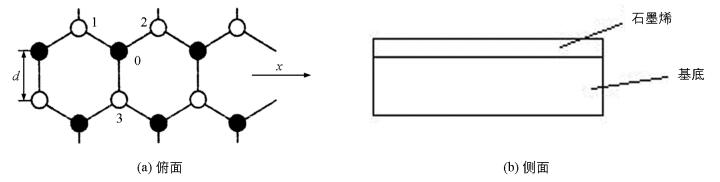
本文研究的系统是在平面状金属(如Cu，Ni)基底上，生成由碳原子构成的理想二维六角形结构的单层石墨烯，其侧面和俯面分别见图 1(a)和(b).

文献[9]在研究外延石墨烯的电导率时，认为碳原子静止，只有电子对电导率有贡献.本研究认为：碳原子在石墨烯平面内在平衡位置附近作非简谐振动，不仅石墨烯碳原子间有相互作用，而且它与金属原子之间也有相互作用.正是这些相互作用和原子的非简谐振动，外延石墨烯的电导率不仅有电子的贡献，而且有离子振动的贡献即声子的贡献.

金属与石墨烯原子之间的相互作用势与原子间距r的关系为

其中：n为键强参数，按文献[13]，取n=1；g为价电子结构有关的量，为简便起见，对碱金属取g=1；r₀为原子间最小距离，可取为C原子半径r_0C与金属离子半径r_om=d-d₀之和，即r₀=r_oC+r_0m；而λ_D为平均德拜波长，与晶格常数a的关系为λ_D≈4.9a.平衡时，金属与石墨烯原子之间距离r₀^′满足

将(2) 式代入(1) 式，求得平衡时金属与石墨烯原子相互作用能φ(r₀^′)，而平均值V_m≈φ(r₀^′).

文献[14]考虑到原子短程相互作用，给出石墨烯一个原子的平均相互作用能为

式中的V₂为两原子的sp₀²轨道σ键的共价能，它与原子间距离d的平方成反比： ${{V}_{2}}=3.26\frac{{{\hbar }^{2}}}{m{{d}^{2}}}=\frac{B}{{{d}^{2}}}$ ，这里：m为自由电子的质量，V₁为金属化能，R=0.154×10⁴(h²/2m)a¹⁰，a₀=4为玻尔半径， $\beta_2 = \frac{2}{3}$ .

因热振动，石墨烯碳原子要在平衡位置d₀附近作微振动，假设基底与石墨烯原子间相互作用不大，则振动情况主要由碳原子间相互作用决定.将φ(d)在平衡位置d₀附近展开，偏离δ=d-d₀很小时，有

将(3) 代入(4) 式，求得原子振动的简谐系数ε₀、第一和第二非简谐系数ε₁，ε₂，其表示式见文献[15].

在零温情况，原子振动很小，振动被“冻结”在基态，声子的贡献σ_p(T)可忽略.

文献[10]采用格林函数法，求出零温(T=0 K)情况下，外延石墨烯的电导率为

式中的e为电子电荷，而b_m⁰，Γ_mF⁰和B⁰分别为

式中：V_m为石墨烯与金属原子的平均相互作用能(V_m≈φ(r₀^′))，ε_F⁰是零温费米能，W_m是金属导带半宽度，在金属作为自由电子近似情况下，与晶格常数a和电子的质量m的关系为

式中：h为普朗克常数，N_m是金属导带可容纳的电子数，对Cu和Ni取N_m=4.

非零温情况下，外延石墨烯电导率σ(T)=σ_e(T)+σ_p(T).文献[9]研究外延石墨烯电导率时，认为碳原子静止，未考虑到声子的贡献，且研究电子电导率时，将费米能作为常量，这里既考虑到声子的贡献，又考虑到费米能随温度的变化.

文献[16]给出费米能与温度的关系为

式中：k_B是玻尔兹曼常数.考虑到电子费米能随温度的变化后，电子电导率为

而b_m，Γ_mF，B分别为

声子对外延石墨烯电导率的贡献，既来源于石墨烯碳原子相互作用，又来源于石墨烯碳原子与基底原子的相互作用，但因后者的相互作用不大，则主要由石墨烯碳原子间相互作用决定.文献[17]应用固体理论，得到声子电导率σ_p(T)，非低温情况下为

低温情况下为

式中：M为碳原子质量；m^*为电子有效质量；k_F为电子费米波矢；c=-2ε_F/3，这里ε_F为费米能；q_m是声子的最大波矢，它与石墨烯原胞面积Ω关系为q_m=(4π/Ω)^1/2；n为自由电子数面密度；θ_D为德拜温度，简谐近似下为 $\theta _{D}^{0}=\left( \frac{\hbar }{{{k}_{\text{B}}}} \right){{\left( \frac{8{{\varepsilon }_{0}}}{3M} \right)}^{\frac{1}{2}}}$ ，考虑到原子非简谐振动后，为^[12]

分别将(13) 式代入(11) 和(12) 式，得到声子电导率随温度T的变化关系.

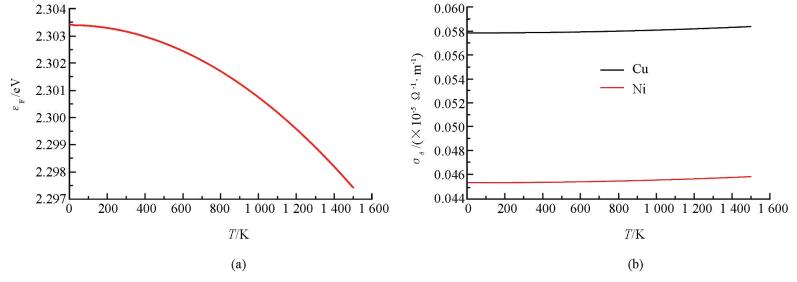
现以在Cu，Ni金属基外延石墨烯为例，研究原子非简谐振动对电导率的影响.文献[18]给出Cu，Ni的点阵常数a，将它代入(7) 式求得W_m.由(1) 式，求得V_m≈φ(r′₀)，数据见表 1.另外，按文献[19]，取ξ=2.38 eV，Cu和Ni一个原胞相应的导带可容纳的电子数N_m=4.文献[10]给出Ω.由石墨烯碳原子间距离d₀=1.42×10^-10 m和文献[19]给出的t=2.8 eV，求得费米速度v_F=0.904 493×10⁶ m/s和 $\varepsilon _{\text{F}}^{0}\text{=}\frac{mv_{\text{F}}^{2}}{2}=2.3034$ eV.将上述数据代入(5) 和(6) 式，求得外延石墨烯的零温电导率σ_m(0)，结果见表 1；将数据代入(9) 式，得到石墨烯电子费米能随温度的变化(图 2(a))，代入(10)、(11) 式，得到电子电导率σ_e(T)随温度的变化(图 2(b)).

由图 2看出：① 石墨烯电子的费米能随着温度的升高而减小，但变化很小.温度从T=300 K升高到T=1 300 K时，费米能只减小1.8%；② 金属基外延石墨烯的零温电导率σ_e(0) 随原子序数增大而增大.原因在于：金属基底原子序数增大时，导带半宽度W_m因晶格常数a变大而变小，金属与石墨烯碳原子相互作用能V_m也变小，基底对石墨烯中电子的约束减弱，因而电导率变大；③ 电子电导率随温度升高而增大，但变化极小，其数量级为10^-5 Ω^-1·m^-1，这与纯石墨烯电子贡献的电导率有区别.原因在于：金属基外延石墨烯电子电导率σ_e除受石墨烯原子影响外，还受到基底原子相互作用能V_m的影响；④ 外延石墨烯电子电导率随温度的变化情况与基底材料有关，在Cu，Ni这2种元素中，以Cu为基底的外延石墨烯电导率随温度的变化较大.

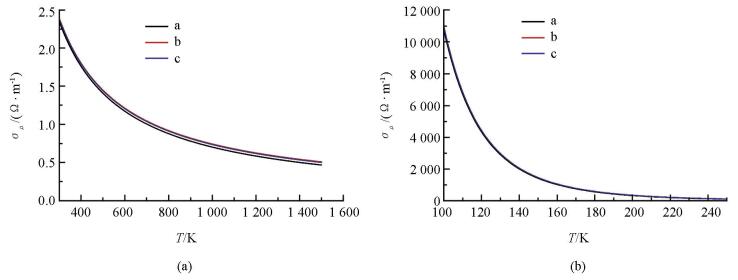
文献[15]已应用(4) 式求得ε₀=3.538 8×10_F² J/m²，ε₁=-3.497 25×10¹² J/m³，ε₂=3.201 40×10²² J/m⁴.又碳原子质量M=1.995 017×10^-26 kg，将它与k_B=1.38×10^-23 J/K，h=1.055×10^-34 J·s等数据代入(13)，求得θ_D0=1 660.02 K.石墨烯碳原子间距离d₀=1.42×10^-10 m，求得Ω=1.746 25×10^-20 m²，q_m=2.681 99×10¹⁰ m^-1，k_F=1.896 38×10¹⁰ m^-1.由前面求的ε⁰，求得 $c=-\frac{2{{\varepsilon }_{\text{F}}}}{3}=-1.5356$ eV.将这些数据代入(11) 和(12) 式，求得外延石墨烯的声子电导率随温度的变化，结果见图 3. 图 3中的曲线a，b和c分别为简谐近似、只考虑到第一非简谐项及同时考虑到第一和第二非简谐项的结果.

由图 3看出：① 外延石墨烯的声子电导率随温度升高而减小，其中，非低温(T＞300 K)时变化较慢，而低温(T＜250 K)时，变化很快；② 简谐近似时，电导率几乎与温度为反比关系.考虑到原子的非简谐振动项后，电导率要比简谐近似的值稍大，而且，温度愈高，非简谐效应愈明显；③ 声子电导率远大于电子，外延石墨烯的总电导率近似等于声子电导率，即σ≈σ_p；④ 与金属块体相比，金属基外延石墨烯的电导率比金属块体要几乎大一个数量级.例如块体Cu的电导率为0.343 Ω^-1·m^-1，而Cu基外延石墨烯的σ=2.394 429 Ω^-1·m^-1；⑤ 本文结果与文献[20]的结果接近，例如：T=295 K时，本文值为σ=2.394 429 Ω^-1·m^-1，与文献[20]的值σ_p=2.230 Ω^-1·m^-1的误差仅为7.37%.此外，本研究得到的外延石墨烯电导率几乎与温度为反比的结论，与电学理论中宏观金属块体的电导率变化规律接近；⑥ 基底对外延石墨烯电导率有一定的影响.在Cu和Ni两种基底中，Cu基底的电导率较大，原因在于：Cu基底金属原子与石墨烯碳原子相互作用能V_m较小，基底对石墨烯中电子的约束减弱，因而外延石墨烯的电导率变大.

本文对金属基外延石墨烯电导率变化规律的研究结果表明：① 零温情况下，金属基外延石墨烯的电导率均为常数，其值与基底元素的原子序数有关，随基底元素原子序数的增大而增大；而非零温情况下，金属基外延石墨烯的电导率均随温度变化而变化.其变化情况既取决于基底元素的性质，又取决于石墨烯和基底元素原子相互作用能的大小，具体关系由(9)-(13) 等式表示；② 金属基外延石墨烯电导率随温度升高而减小，其中，温度较低时(T＜300 K)时，变化较快，而温度较高时则变化很慢.它的电导率包括声子的贡献和电子的贡献两部分，其中电子的贡献很小且随温度的变化也很小，声子贡献的电导率远大于电子且随温度变化较大；③ 原子的非简谐振动有重要的影响：简谐近似下，电导率随温度升高而减小，几乎成反比关系.考虑到原子非简谐项后，电导率随温度升高而减小的变化速度减慢.温度愈高，原子振动非简谐效应愈明显.