高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

基于神经元晶体管和忆阻器的Hopfield神经网络及其在联想记忆中的应用

,  ,  , 

上一篇

下一篇

朱航涛, 王丽丹, 段书凯, 等. 基于神经元晶体管和忆阻器的Hopfield神经网络及其在联想记忆中的应用[J]. 西南大学学报（自然科学版）, 2018, 40(2): 157-166. doi: 10.13718/j.cnki.xdzk.2018.02.022
引用本文: 朱航涛, 王丽丹, 段书凯, 等. 基于神经元晶体管和忆阻器的Hopfield神经网络及其在联想记忆中的应用[J]. 西南大学学报（自然科学版）, 2018, 40(2): 157-166. doi: 10.13718/j.cnki.xdzk.2018.02.022
shu
Hang-tao ZHU, Li-dan WANG, Shu-kai DUAN, et al. A Hopfield Neural Network Based on Neuron Transistor and Memristor and Its Application in Associative Memory[J]. Journal of Southwest University Natural Science Edition, 2018, 40(2): 157-166. doi: 10.13718/j.cnki.xdzk.2018.02.022
Citation: Hang-tao ZHU, Li-dan WANG, Shu-kai DUAN, et al. A Hopfield Neural Network Based on Neuron Transistor and Memristor and Its Application in Associative Memory[J]. Journal of Southwest University Natural Science Edition, 2018, 40(2): 157-166. doi: 10.13718/j.cnki.xdzk.2018.02.022
shu

基于神经元晶体管和忆阻器的Hopfield神经网络及其在联想记忆中的应用

  • 西南大学 电子信息工程学院/非线性电路与智能信息处理重庆市重点实验室，重庆 400715

  • 基金项目: 国家自然科学基金项目(61571372)；国家自然科学基金面上项目(61672436)；重庆市基础科学与前沿技术研究专项重点项目(cstc2017jcyjBX0050)；教育部中央高校基本科研业务费专项创新团队项目(XDJK2014A009)；教育部中央高校基本科研业务费专项创新团队项目(XDJK2016A001)
详细信息
    作者简介:

    朱航涛(1990-)，男，浙江永康人，硕士研究生，主要从事非线性电路与系统的研究 .

    通讯作者: 王丽丹，教授，博士研究生导师; 

  • 中图分类号: TP183

A Hopfield Neural Network Based on Neuron Transistor and Memristor and Its Application in Associative Memory

  • School of Electronic and Information Engineering/Chongqing Key Laboratory of Nonlinear Circuits and Intelligent Information Processing, Southweat University, Chongqing 400715, China

  • 摘要: 随着人工智能的高速发展，越来越多的神经元模型相继被提出，现有的神经元电路主要由普通晶体管、运算放大器等高功耗器件构成，存在结构复杂、集成度不高、兼容性差、功耗高、阈值调节难度高的缺点.针对以上不足，首次提出了一种全新的神经元结构，该结构仅由神经元晶体管、忆阻器和普通电阻构成，相比传统神经元电路，不包含复杂的差分运算电路以及电流与电压信号的转换电路，电路结构简单，同时具有良好的电路兼容性，可用于大规模集成.该结构利用神经元晶体管的加权求和特性以及阈值可控功能来模拟神经元信息传导过程，同时利用阈值忆阻器的阈值特性和阻值连续变化能力来设定和更新突触权值，使得该新型神经元结构不仅能实现传统神经元电路功能的同时，还具有能耗低、阈值动态可控、权值可编程的优点，不仅极大地简化了网络结构，还能加强网络性能.其次，还提出了基于这种新型神经元结构的忆阻离散Hopfield神经网络，该忆阻神经网络有助于促进人工神经形态系统的硬件实现，使神经网络系统能耗降低，集成度极大地提高，将这种网络运用在联想记忆和彩色数字图像恢复中，进一步说明了基于全新神经元结构的忆阻离散hopfield神经网络的实用性以及有效性.
    Abstract: With the development of artificial intelligence, more and more models of neurons have been proposed. The existing neuronal circuits are made of some high power consumption devices such as transistors and operational amplifiers, which have the disadvantages of complex structure, low integration, poor compatibility, high power consumption and difficulty in threshold adjustment. Given this situation, the authors of this paper put forward, for the first time, a novel neuron structure that consists only of a neuMOS, memristors and resistances. Compared to the traditional circuits of neurons, this circuit has simpler structure. It has no differential operational circuits and switching circuits, but has good compatibility, low power consumption and VLSI application. This structure utilizes the weighted summation and threshold-controllable features of neo-MOS to simulate the synaptic transmission between neurons, and the threshold characteristics and continuous change of memristance to set and update synaptic weight. The new neuron structure can achieve the function of traditional neuronal circuits, and has the advantages of low power consumption, threshold control and weight programmability, thus greatly simplifying the network structure and enhancing network performance. In addition, this paper proposes a novel discrete Hopfield neural network based on the neuron structure called Mem-Hopfield. That promotes neural morphological system of neural networks hardware implementation with lower consumption and higher integration. The effectiveness and practicability of the new optimized neural circuit construction is proved further by applying the Mem-Hopfield neural network in associative memory and color digital image recovery.
  • 加载中

  • 图 1  神经元结构

    下载: 全尺寸图片 幻灯片

    图 2  neuMOS结构图

    下载: 全尺寸图片 幻灯片

    图 3  三输入neuMOS的SPICE模型

    下载: 全尺寸图片 幻灯片

    图 4  neuMOS阈值控制输入输出曲线

    下载: 全尺寸图片 幻灯片

    图 5  阈值自适应忆阻器

    下载: 全尺寸图片 幻灯片

    图 6  阈值忆阻器

    下载: 全尺寸图片 幻灯片

    图 7  忆阻离散Hopfield神经网络

    下载: 全尺寸图片 幻灯片

    图 8  三神经元忆阻离散Hopfield神经网络突触权值设定过程

    下载: 全尺寸图片 幻灯片

    图 9  基于neuMOS和忆阻器的Hopfield神经网络联想记忆仿真结果

    下载: 全尺寸图片 幻灯片

    图 10  8位色阶的联想记忆

    下载: 全尺寸图片 幻灯片

    图 11  基于neuMOS和忆阻器的Hopfield神经网络彩色数字恢复

    下载: 全尺寸图片 幻灯片

    表 1  外部激励电流幅值模型参数表

    Roff/kΩ Ron/Ω koff/(nm·s-1) kon/(nm·s-1) aoff aon ioff/μA ion/μA αon αoff
    1 5 0 1.46e-9 -4.68e-13 0.2 0.8 300 -30 30 30
    下载: 导出CSV
  • [1] SHIBATA T, OHMI T. A Functional MOS Transistor Featuring Gate-Level Weighted Sum and Threshold Operations [J]. IEEE Transactions on Electron Devices, 1992, 39(6): 1444-1455. doi: 10.1109/16.137325
    [2] SHIBATA T, OHMI T. An Intelligent MOS Transistor Featuring Gate-Level Weighted Sum and Threshold Operations [C] //Electron Devices Meeting, 1991. IEDM'91. Technical Digest. International. IEEE Xplore. Washington: 1992: 919-922.
    [3] ISHII H, SHIBATA T, KOSAKA H, et al. Hardware-Back Propagation Learning of Neuron MOS Neural Networks [C] //Electron Devices Meeting, 1992. IEDM'92. Technical Digest. International.IEEE Xplore, 1993: 435-438.
    [4] SHIBATA T, KOSAKA H, ISHII H, et al. A Neuron-MOS Neural Network Using Self-Learning-Compatible Synapse Circuits [J]. IEEE Journal of Solid-State Circuits, 1995, 30(8): 913-922. doi: 10.1109/4.400434
    [5] OKADA A, SHIBATA T. A Neuron-MOS Parallel Associator for High-Speed CDMA Matched Filter [C] //IEEE International Symposium on Circuits and Systems. Orlando: IEEE, 1999: 392-395.
    [6] doi: https://www.sciencedirect.com/science/article/pii/S0026271497000048 SHIBATA T, AU R, et al. Neuron-MOS Multiple-Valued Intelligent Memory Technology [J]. Ieice Technical Report Computer Systems, 1994, 94: 1-8.
    [7] doi: http://todaes.acm.org/archive.cfm?id=2830627 ZHANG R, KANEKO M. Robust and Low-Power Digitally Programmable Delay Element Designs Employing Neuron-MOS Mechanism [J]. Acm Transactions on Design Automation of Electronic Systems, 2015, 20(4): 1-19.
    [8] CHUA L O. Memristor-The missing circuit element [J]. IEEE Transactions on Circuit Theory, 1971, 18(5): 507-519. doi: 10.1109/TCT.1971.1083337
    [9] 高士咏, 段书凯, 王丽丹.忆阻细胞神经网络及图像去噪和边缘提取中的应用[J].西南大学学报(自然科学版), 2011, 33(11): 63-70. doi: http://xbgjxt.swu.edu.cn/jsuns/jsuns/ch/reader/view_abstract.aspx?file_no=xnnydxxb201111012&flag=1
    [10] PICKETT M D, STRUKOV D B, BORGHETTI J L, et al. Switching Dynamics in Titanium Dioxide Memristive Devices [J]. Journal of Applied Physics, 2009, 106(7): 074508. doi: 10.1063/1.3236506
    [11] doi: http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6895305 PAPANDROULIDAKIS G, VOURKAS I, VASILEIADIS N, et al. Boolean Logic Operations and Computing Circuits Based on Memristors [J]. Circuits & Systems Ⅱ Express Briefs IEEE Transactions on, 2014, 61(12): 972-976.
    [12] KIM H, SAH M P, YANG C, et al. Memristor Bridge Synapses [J]. Proceedings of the IEEE, 2012, 100(6): 2061-2070. doi: 10.1109/JPROC.2011.2166749
    [13] KVATINSKY S, FRIEDMAN E G, KOLODNY A, et al. TEAM: Threshold Adaptive Memristor Model [J]. IEEE Transactions on Circuits and Systems Ⅰ: Regular Papers, 2013, 60(1): 211-221. doi: 10.1109/TCSI.2012.2215714
    [14] KVATINSKY S, RAMADAN M, FRIEDMAN E G, et al. VTEAM: A General Model for Voltage-Controlled Memristors [J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2015, 62(8): 786-790. doi: 10.1109/TCSII.2015.2433536
  • 加载中
图( 11) 表( 1)
计量
  • 文章访问数:  1364
  • HTML全文浏览数:  575
  • PDF下载数:  487
  • 施引文献:  0
出版历程
  • 收稿日期:  2016-12-05
  • 刊出日期:  2018-02-20

基于神经元晶体管和忆阻器的Hopfield神经网络及其在联想记忆中的应用

    通讯作者: 王丽丹，教授，博士研究生导师; 
    作者简介: 朱航涛(1990-)，男，浙江永康人，硕士研究生，主要从事非线性电路与系统的研究
  • 西南大学 电子信息工程学院/非线性电路与智能信息处理重庆市重点实验室，重庆 400715
  • 收稿日期:  2016-12-05
基金项目:  国家自然科学基金项目(61571372)；国家自然科学基金面上项目(61672436)；重庆市基础科学与前沿技术研究专项重点项目(cstc2017jcyjBX0050)；教育部中央高校基本科研业务费专项创新团队项目(XDJK2014A009)；教育部中央高校基本科研业务费专项创新团队项目(XDJK2016A001)

摘要: 随着人工智能的高速发展，越来越多的神经元模型相继被提出，现有的神经元电路主要由普通晶体管、运算放大器等高功耗器件构成，存在结构复杂、集成度不高、兼容性差、功耗高、阈值调节难度高的缺点.针对以上不足，首次提出了一种全新的神经元结构，该结构仅由神经元晶体管、忆阻器和普通电阻构成，相比传统神经元电路，不包含复杂的差分运算电路以及电流与电压信号的转换电路，电路结构简单，同时具有良好的电路兼容性，可用于大规模集成.该结构利用神经元晶体管的加权求和特性以及阈值可控功能来模拟神经元信息传导过程，同时利用阈值忆阻器的阈值特性和阻值连续变化能力来设定和更新突触权值，使得该新型神经元结构不仅能实现传统神经元电路功能的同时，还具有能耗低、阈值动态可控、权值可编程的优点，不仅极大地简化了网络结构，还能加强网络性能.其次，还提出了基于这种新型神经元结构的忆阻离散Hopfield神经网络，该忆阻神经网络有助于促进人工神经形态系统的硬件实现，使神经网络系统能耗降低，集成度极大地提高，将这种网络运用在联想记忆和彩色数字图像恢复中，进一步说明了基于全新神经元结构的忆阻离散hopfield神经网络的实用性以及有效性.

English Abstract

    全文HTML

  • 1991年，日本东北大学的柴田直(Tadashi Shibat)教授和大见忠弘(Tadahiro Ohmi)博士基于浮栅MOS结构提出了神经元MOS晶体管(缩写为neuMOS)[1].这种器件的结构和功能非常类似于人工神经网络[2]，其具有多输入信号控制、阈值可变可控、制造工艺兼容、功耗低、可简化电路结构和节省芯片面积等特点，被广泛应用于神经网络[3-4]、匹配滤波[5]、逻辑运算[6]、低功耗电路[7]等电路中.另一方面，忆阻器作为第四个基本电路元件被提出[8]，它具有阻值连续可调、断电非易失、低功耗等特性，忆阻器是天然的电子突触，可以实现权值的连续更新，是模仿神经系统的最佳选择.

    人工神经网络作为一种新型的信息处理系统，可以通过软件和硬件两种方式来实现.软件实现的方式对计算机要求高，而且存在并行程度低、运行速度慢的缺点，无法满足实时性要求.相比较而言，利用电子元器件搭建起来的神经网络更能满足实际的需求，而且充分体现了并行、高速的特点.但是在当前的神经网络硬件电路实现中[9]，基本上都是采用普通MOS管、电阻、电容、运算放大器等元器件实现的，存在电路结构复杂、功耗高、互连性低的缺点.

    本文基于neuMOS和阈值忆阻器[10-11]提出了一种全新的神经网络结构，这种由neuMOS晶体管和忆阻突触电路组成的网络结构简单、神经元阈值可调、突触权值可连续更新，极大地简化了网络结构，增强了网络性能.而且，这种结构除了neuMOS、忆阻器和电阻外，不包含其他元件，具有很好的电路兼容性.同时，本文还验证了基于这种全新神经元结构的Hopfield神经网络在联想记忆和彩色数字恢复中的应用.

1.   基于neuMOS和忆阻器的忆阻神经元

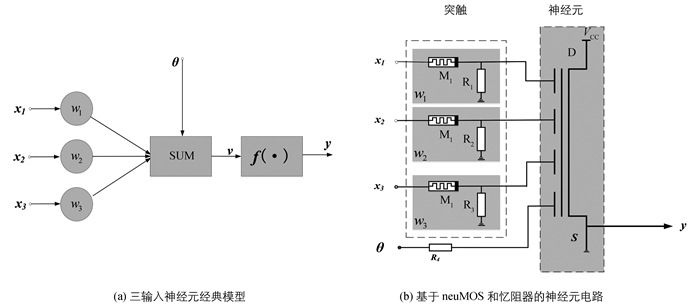
  • 神经元是神经网络信息处理的基本单元，图 1(a)显示了三输入一输出的经典神经元模型.其中xi(i=1，2，3)为神经元输入，wi(i=1，2，3)是神经元的突触权值，v是输入信号的线性组合输出，阈值为θ，激活函数为f(·)，y是神经元的输出信号.等式(1)是这种神经元模型的更新方式，y=sign(·)为符号函数.

    根据这种经典模型，本文提出的结构如图 1(b)所示.该结构由neuMOS、忆阻器和电阻组成，忆阻器和普通电阻组成的分压电路作为突触，利用neuMOS的加权求和特性和阈值导通特性来实现神经元的线性组合以及激活函数功能，而θ端的电压充当神经元阈值的作用.相比较于现有的神经元电路结构[12]，这种电路复杂度低，省去了大部分的电阻、晶体管和所有的运算放大器，避免了复杂的减法运算，也不需要电压电流之间的转换. neuMOS晶体管的制造只需要标准的双层多晶硅工艺，与标准的CMOS工艺可以很好地兼容，在电路集成方面具有突出的优势.另外，利用neuMOS的特点，这种神经元的各个输入信号根据电容耦合系数来计算加权和，这种方式只有在电容充放电的时候会有电流，再加上忆阻器本身具有低功耗特性，因此，相比较于电流型加权求和电路，可以大大降低电路能耗.同时，这种神经元具有一个阈值控制端，通过外加电压可以改变整个神经元的阈值特性.可见，这种全新的神经元不仅简化了网络结构，还增强了网络性能，具有很强的研究价值.为了对这种神经元能有更深入地认识，我们分神经元特性和突触两部分来介绍工作原理.

    • 1.1.   神经元特性

  • 神经元必须具有线性组合器来叠加各个输入信号的加权和以及一个激活函数来限制神经元的输出.在往常的设计中，都需要通过复杂的模拟电路来实现这部分的功能，在一定程度上已经成为了大规模集成神经网络的瓶颈.这里利用了neuMOS的突出优势，简单地改变输入方式和控制方法，就能有效地达到本文的设计目的.下面以三输入neuMOS为例进行仿真来说明设计的有效性.

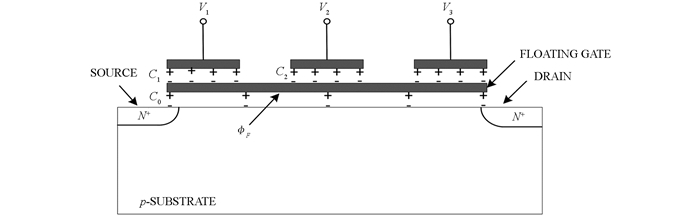
    图 2为三输入neuMOS的结构图，与普通MOS管相比，它由多个门极输入端组成，门极输入端与浮栅之间通过电容耦合.其中ϕF是浮栅电压，Ci(i=1，2，3)是浮栅和第i个输入栅之间的电容，Vi(i=1，2，3)是第i个输入栅上所加的电压. C0是浮栅和衬底间的电容.浮栅上的电压ϕF由等式(2)决定[1].

    当电压ϕF大于neuMOS阈值VTH时，MOS管导通.即neuMOS导通的条件为

    为了实现神经元多输入加权求和以及阈值导通功能，我们对neuMOS做如下处理：V1和V2端作为神经元的两个输入，为了便于分析和观察，权值都为1，V3做为神经元阈值调整端，neuMOS导通与否用来模拟非线性函数f(·)，即符号函数.取

    将不等式(3)表示成V1、V2与V3的关系式：

    VTH为neuMOS的固有阈值，VTH*为neuMOS的等效阈值.当输入端的和大于等效阈值时，neuMOS导通，等效阈值由阈值控制端V3的电压决定，达到阈值可编程的目的.

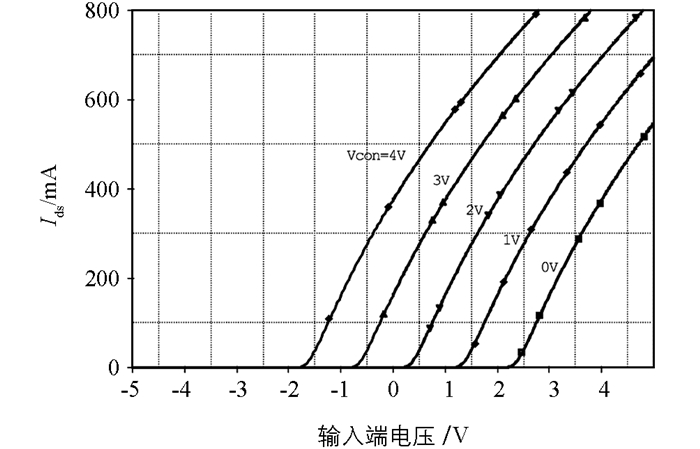
    图 3是三输入neuMOS的SPICE模型，固有阈值电压设定为0.6 V，改变阈值控制端V3的电压，得到如图 4所示的输入输出关系图.横坐标为输入端的电压和(V1+V2)，纵坐标为neuMOS的导通电流(Ids).当有电流产生时，说明晶体管处于导通状态.在V3的电压从4 V到0 V的变化过程中，neuMOS的等效阈值相应地发生改变，也就是说，neuMOS导通电压临界值随着V3成正相关地线性变化，这个特性能够很直观地模拟神经元的兴奋传递，且具有阈值可调节的功能.

    • 1.2.   忆阻突触特性

  • 根据神经元特性和电路分压公式，我们得到神经元输入加权和为

    令：

    则有

    wi(i=1，2，3)为突触权值，公式中的忆阻器采用的是电流阈值自适应忆阻模型(TEAM)[14-15]，其状态变量微分方程、窗函数表达式和忆阻值表达式分别如等式(8)，(9)，(10)所示：

    koff和kon表示幅度参数，koff为正，kon为负；αon和αoff为匹配参数，皆为常数；ioff和ion分别表示开关时的电流阈值.

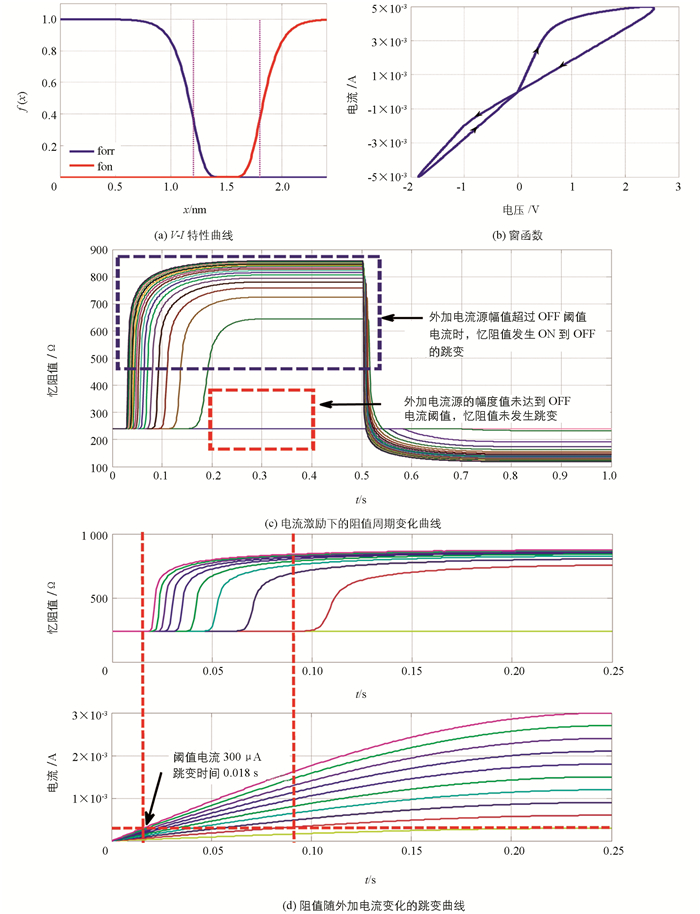
    图 5(a)(b)是TEAM模型在外部电流正弦信号5sin(2πt)mA激励下的伏安特性曲线和窗函数，图 5(c)(d)是在外部电流正弦信号Iinput=Iampsin(2πt)下的忆阻器阻值变化曲线，Iamp范围在[0，200 0 μA]，其他设置参数如表 1.

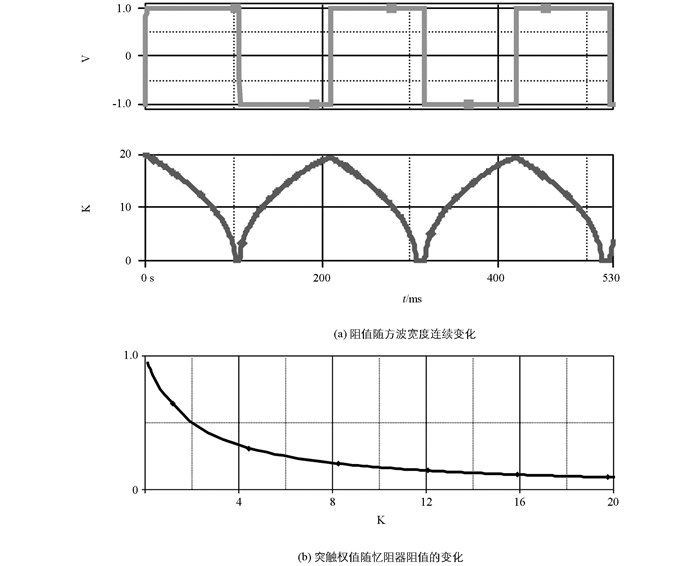
    从图中可以看出，随着电流的不断增加，当通过忆阻器的电流达到300 μA后，忆阻器阻值开始变化，而当外加电流未达到ioff阈值电流时，忆阻值将维持初始的忆阻值不变.利用这个特性，当我们给忆阻器加正负1V的方波电压时(忆阻器最大阻值设定为2K，此时的最小电流大于忆阻器阈值电流)，阻值随着方波宽度连续变化，如图 6(a)所示.可见，阈值忆阻器具有阻值可编程的能力，而且能够实现连续变化，能够实现权值的连续更新，是天然的电子突触器件.随着忆阻器阻值的改变，突触权值在(0.05，0.95)的范围内连续变化，如图 6(b).

2.   忆阻离散Hopfield神经网络

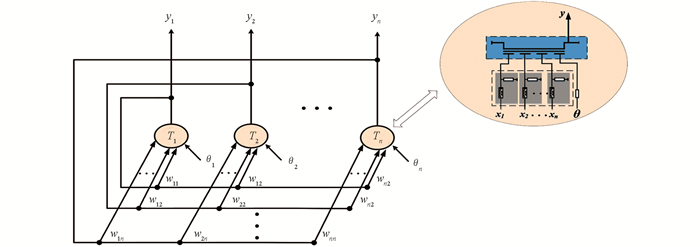
  • 本文提出的忆阻离散Hopfield神经网络如图 7所示，其中y=(y1，y2…yn)，θ=(θ1，θ2…θn)分别表示神经元状态和阈值. wij为第i和第j个神经元互联权值，为了满足稳定性要求，权值必须满足如下条件，即网络为对称连接且自身无连接.

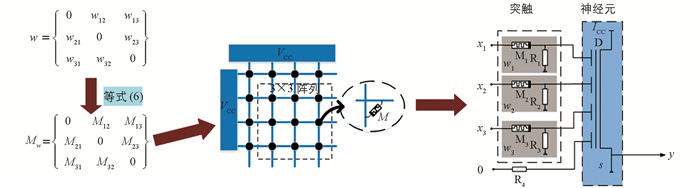
    wij由式(6)决定，也就是说，按网络需要来对忆阻器阻值进行编程，即可得到相应的突触权值，则权值矩阵可以由相应的存有相应阻值的忆阻器阵列决定.三神经元忆阻离散Hopfield神经网络突触权值设定的整个过程如图 8所示.

    这种全新的神经网络结构的工作方式是异步的，其步骤可归纳为下面5步：

    ① 网络初始化，包括忆阻器阻值设定(权值设定)和θ设定(阈值设定)；

    ② 从网络中随机选取一个神经元i；

    ③ 求出该神经元i的输入，y(t)表示在t时刻的状态；

    ④ 求出该神经元i的输出，此时网络中其他神经元输出保持不变；

    ⑤ 判断网络是否达到稳点状态，如果满足则结束，否则转到第②步.

    相比较于传统的Hopfield神经网络，本文提出的忆阻离散Hopfield神经网络在电路结构、系统集成和能耗上具有无法比拟的优势.首先，整个网络只有忆阻器、电阻和neuMOS 3种器件组成，大大简化了原来复杂的晶体管电路.另外，由于忆阻器和neuMOS的低能耗特性，以及整个网络省去了大部分电阻、晶体管和全部运算放大器等耗能元件，使得整个网络在节能方面有突出优势.这种优势更有利于神经网络系统的大规模集成，也更适应于VLSI的要求.

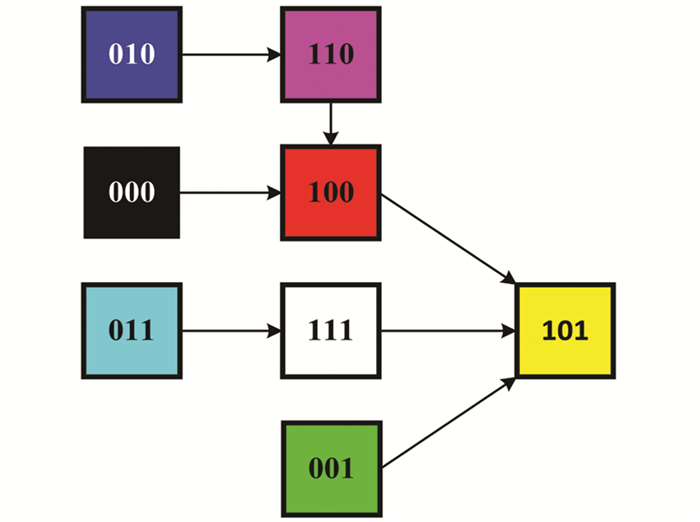
3.   忆阻离散Hopfield神经网络在联想记忆及彩色数字图像恢复中的应用

  • 为了证明忆阻离散Hopfield神经网络的有效性，我们对其联想记忆能力进行了仿真.我们用3位0/1串来表示3种基础色，第1位表示红色，第2位表示绿色，第3位表示蓝色，1代表有这种颜色，0代表没有这种颜色.则可以用这3位0/1串表示出8种常用的颜色，分别为黑色(000)、绿色(001)、蓝色(010)、青色(011)、红色(100)、黄色(101)、紫色(111)和白色(111).我们设定联系记忆的最终结果为“黄色”，则该神经网络的权值矩阵和阈值向量分别设定为

    根据突触权值设定过程，我们可以得到相应的忆阻器阻值和阈值控制端输入电压，其中，R1=R2=R3=R4=2 kΩ：

    实验中，每一次状态的改变都按照上一节所提到的步骤来实现.仿真结果如图 9所示，在一个更新周期内，只有一位神经元的状态被更新，每一个初始状态最终都能成功地恢复到稳态“101”.比如初始输入为蓝色(010)，第一个更新周期中，第一个神经元“0”的状态按照式(1)的更新规则更新为“1”，即为“110”；第二个更新周期中，第二个神经元“1”的状态按照式(1)的更新规则更新为“0”，即为“100”；第三个更新周期中，第三个神经元“0”的状态按照式(1)的更新规则更新为“1”，即为“101”，最终输出“黄色”稳态.当然，我们也可以设置不同的忆阻器值和θ端电压来实现其他状态.

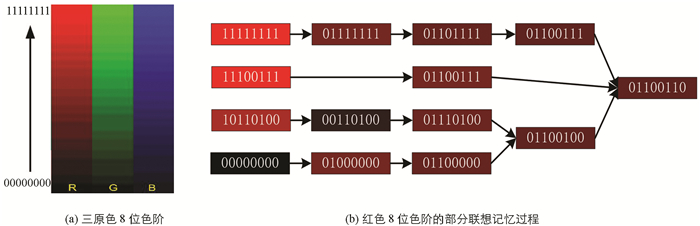
    实际的8位彩色图像中，分别用2∧8(即256)个阶度表示红绿蓝，每个颜色的取值范围都是[0, 255]，如图 10(a)所示，理论上共有256×256×256种颜色.同三原色的联想记忆方法一样，我们构建了八神经元忆阻离散Hopfield神经网络来实现对每一种颜色色阶的联想记忆.假设我们要联想的结果为红色的“01100110”，图 10(b)给出了部分联想记忆过程.

    利用上述的实验原理，我们将这种全新的忆阻离散Hopfield神经网络应用到彩色数字恢复图像中.对于一个10*9像素构成的数字图像，每一个像素点都由R，G，B 3层组成.对于背景区域，最后的稳态为黑色，即每一层的值都为“0”.对于数字区域，最后的稳态根据要求来设定.通过设定不同的忆阻器值和θ端电压，即可恢复受噪声干扰的彩色数字图像.如图 11所示，我们给彩色数字图像随机加上噪声，使得原图像变得不易识别，然后将背景区域和数字区域分别通过学习好的神经网络，最后得到除噪后的数字图像.

4.   结论

  • 本文基于neuMOS和忆阻器提出了一种全新的神经元结构，该结构具有神经元的加权求和特性和阈值导通特性，能够完全模拟神经元信息传导过程.在电路组成上，这种神经元只有neuMOS、忆阻器和电阻3种元器件，省去了传统神经元电路中复杂的差分运算电路以及电流信号和电压信号之间的转换电路，所以电路结构简单且具有很好的电路兼容性，适合大规模集成.由于neuMOS和忆阻器的优越性能，使得这种神经元能耗低、阈值动态可控、权值可编程，不但能极大地简化网络结构，还能增强网络性能.为了验证这种神经元的神经网络特性，本文构建了基于neuMOS和忆阻器的全新神经元的忆阻离散Hopfield神经网络，并验证了其联想记忆的能力，以及实现了其在彩色数字图像恢复中的应用.

参考文献 (14)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回