其中：x(t)，y(t)，z(t)分别表示正常食饵、突变食饵和捕食者的密度; d₁(t)，d₂(t)，d₃(t)，β(t)，k(t)是正的τ-周期函数，且d₁(t)，d₂(t)，d₃(t)分别表示正常食饵、突变食饵和捕食者的死亡率，β(t)表示捕食者对正常食饵的消化率，k(t)表示捕食者捕食正常食饵所获营养的转化率，出生和捕获均是τ周期的; μ₁和μ₂(0≤μ₁，μ₂≤1)分别表示在时刻t=(n+l)τ，0＜l＜1，n∈ $\mathbb{N} $₊处对突变食饵的捕杀努力量和对捕食者的捕获努力量; a，b(0＜b＜a＜1)分别表示正常种群的内禀增长率和密度依赖率; 0≤θ＜1表示正常食饵的基因突变率; (1-θ)x(t)(a-bx(t))，θx(t)(a-bx(t))分别表示在t=(n+1)τ，n∈$\mathbb{N} $₊时刻正常食饵和突变食饵的出生.

定理1   集合$\Omega \subseteq \mathbb{R}_{+}^{3} $是系统(1)的一个不变区域，其中

证  令(x(t)，y(t)，z(t))是系统(1)具有严格正初值(x₀，y₀，z₀) $ \subseteq \Omega $的解.对t∈(0，τ]，$x\left( t \right)\le {{x}_{0}}{{\rm{e}}^{\rm{-}\int_{0}^{t}{{{d}_{1}}\left( s \right)\rm{d}s}}} $，由

可得

所以

由b＞0，0＜θ＜1，上面的二次多项式在0＜x(τ)＜$\frac{a}{b} $内单调递增，所以得到0＜x(τ⁺)＜$\frac{a}{b} $，再由系统(1)的周期性，可得到对所有的t≥0有0＜x(t)＜$\frac{a}{b} $.

对t∈(0，τ]，y(t)= $ {{y}_{0}}{{\rm{e}}^{\rm{-}\int_{0}^{t}{{{d}_{2}}\left( s \right)\rm{d}s}}}$.由y₀＞0，0≤μ₁≤1，0＜x(τ)＜$\frac{a}{b} $可得

再由系统(1)的周期性，可得到对所有的t≥0有y(t)＞0.

对t∈(0，τ]，z(t)= ${{z}_{0}}{{\rm{e}}^{\int_{0}^{t}{\left( -{{d}_{3}}\left( s \right)\rm{+}k\left( s \right)\beta \left( s \right)x\left( s \right) \right)\rm{d}s}}} $.由z₀＞0，0≤μ₂≤1，得

再由系统(1)的周期性，可得到对所有的t≥0有z(t)＞0.得证.

下面给出系统(1)的子系统(2)的一些基本性质：

令

显然A＜1，B＜1.则可得到系统(2)的频闪映射为：

易知(3)式始终存在不动点G₁(0，0)，且当[1+a(1-θ)]A＞1成立时，(3)式还存在正不动点G₂(x^*，y^*)，其中

定理2   (ⅰ)如果[1+a(1-θ)]A＜1成立，则系统(2)的平凡周期解(0，0)是全局渐近稳定的;

(ⅱ)如果[1+a(1-θ)]A＞1成立，则系统(2)的具有正初值(x^*，y^*)的周期解(x_p(t)，y_p(t))是全局渐近稳定的.

证  为了得到系统(2)周期解的稳定性，只需考虑系统(3)的不动点的稳定性.记

则(3)式的线性化表达为

其中

当M的特征根的模小于1时，G₁(0，0)和G₂(x^*，y^*)局部渐近稳定.而M仅需满足下面的Jury条件^[12]：

如果[1+a(1-θ)]A＜1成立，G₁(0，0)是(3)式唯一的非负不动点，且有

易知

显然

进一步有

即G₁(0，0)局部稳定，进而系统(2)的平凡周期解(0，0)是全局渐近稳定的.

(ⅱ)如果[1+a(1-θ)]A＞1成立，G₁(0，0)不稳定. G₂(x^*，y^*)存在，且

其中

由0＜a，θ，A＜1得

所以

显然

进一步有

即G₂(x^*，y^*)局部稳定，进而系统(2)的周期解(x_p(t)，y_p(t))是全局渐近稳定的.

由定理2的结论可得系统(1)解的性质如下：

定理3    (ⅰ)如果[1+a(1-θ)]A＜1成立，则系统(1)的平凡周期解X₁=(0，0，0)是全局渐近稳定的;

(ⅱ)如果[1+a(1-θ)]A＞1成立，则系统(1)的捕食者种群灭绝周期解X₂=(x_p(t)，y_p(t)，0)是全局渐近稳定的.

本部分主要通过数值模拟探讨食饵种群突变率对整个系统动力学行为的影响.数值模拟中模型的参数、函数及初值取为：a=0.7，b=0.05，μ₁=0.7，μ₂=0.05，l=0.25，τ=1. d₁(t)=0.1+0.001sin t，d₂(t)=0.2+0.002sin t，d₃(t)=0.1+0.001sin t，k(t)=0.5+0.001cos t，β(t)=0.05+0.000 1cos t. x₀=1，y₀=0.2，z₀=0.5.

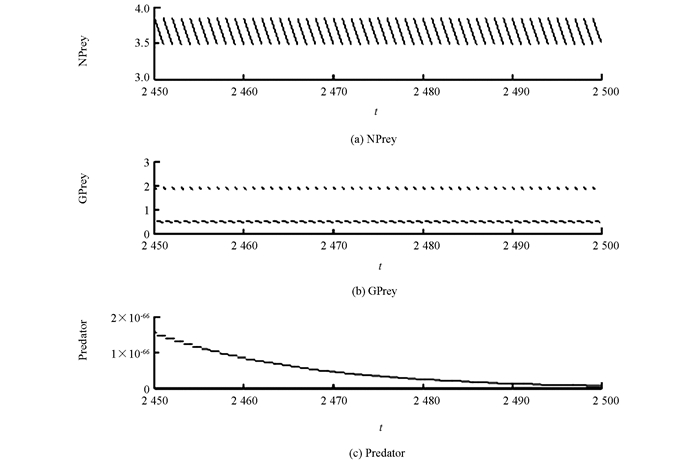
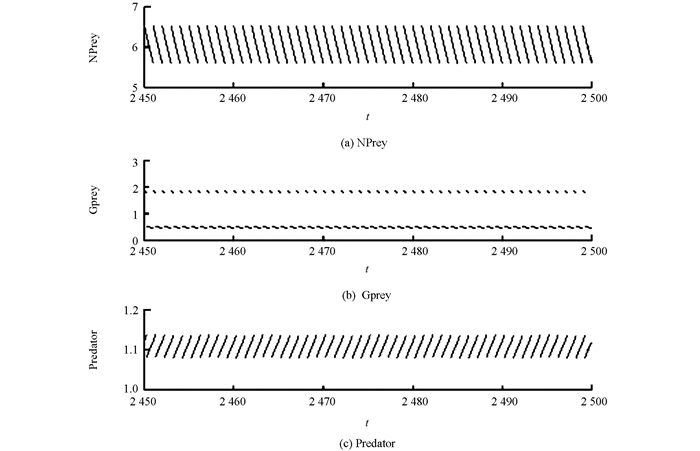
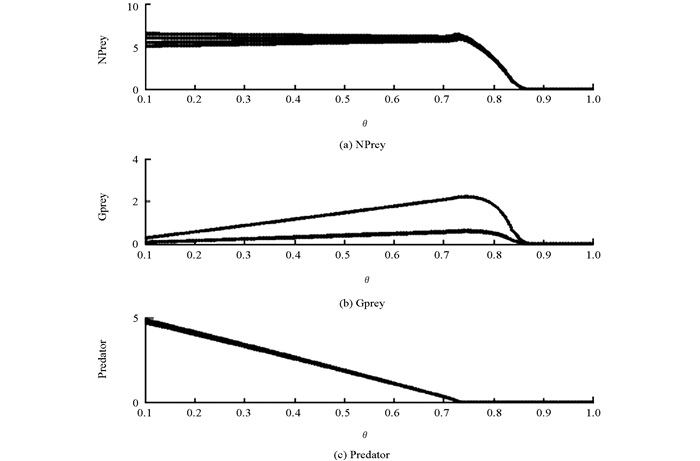
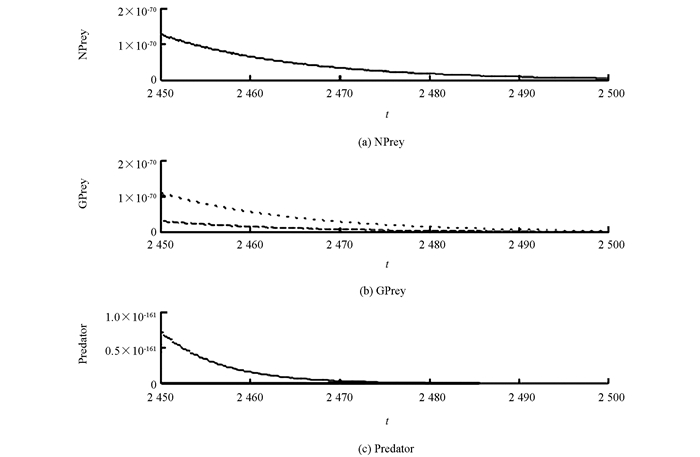
从仿真实验可看出突变率θ的不同取值对应了系统(1)不同的动力学行为.由图 1知当θ=0.95时，系统(1)中的种群全部灭绝.由图 2知当θ=0.8时，系统(1)中的捕食者种群灭绝.由图 3知当θ=0.6时，系统(1)是持续生存的.为了更好地反映突变率对整个系统解的影响，图 4显示了以突变率作为分支参数的分支图.

从图 4能够清楚地看到存在两个阈值θ₁^*和θ₂^*(θ₂^*＞θ₁^*)，使得当θ＞θ₂^*时，系统中所有的种群灭绝.此时由于食饵突变率非常大，导致正常食饵种群急剧减少，进而导致捕食者减少，并且突变食饵被脉冲捕杀，因而整个种群会灭绝.当θ₁^*＜θ＜θ₂^*时，捕食者种群灭绝.此时食饵突变率较大，使得正常食饵种群量较少，以致无法满足捕食者的生存需求，因而捕食者种群会灭绝.当θ＜θ₁^*时，系统持续生存.此时食饵突变率较小，正常的食饵种群可以保证捕食者的生存，因而所有种群持续生存.综上，系统(1)对食饵种群的基因突变率很敏感，这对生物多样性有很重要的影响，所以应该加强环境保护力度以减小种群发生基因突变的可能性，这样才能实现生物的可持续发展.