-
近年来,以Co,Fe以及FeCo为主体的铁磁性薄膜的微波电磁特性研究[1-2]受到很大关注,BEILLE J等人在文献[3]中提出将Co原子掺杂进窄带半导体FeSi中,可以实现Co,Fe替换,并且发现Fe1-xCoxSi化合物在x=0.02时会出现金属-绝缘体转变.目前对Fe1-xCoxSi合金的研究,主要是在磁性等方面[4-7],而对其热力学性质研究较少.文献[8]利用德拜模型,计算了强关联的二元合金FeSi的热学性质;文献[9]计算了二元合金FeSi和CoSi的弹性模量,但均未对掺杂Co的三元合金Fe1-xCoxSi的热力学性质进行探讨;文献[10]通过自洽热力学模型,对Fe1-xCoxSi的热学性质进行了研究,发现在只考虑简谐近似下,其结果与实验值有一定差距,且不能描述弹性模量、热容量等这些重要参数的变化规律,并揭示出非简谐效应的重要性.为此,本研究将考虑非简谐效应,应用热力学和固体物理理论,对Fe1-xCoxSi合金热力学性质进行探讨.
全文HTML
-
本文研究的合金是由n摩尔的二元合金FeSi中,掺有Co后,Co原子部分替代合金中的Fe原子,设掺杂原子浓度为x,则Fe原子浓度为1-x,合金摩尔体积为v,处于温度为T、压强为p的环境中,在平衡位置附近原子相互作用势为
式中:r0为Fe与Si原子的平衡距离;振动距离r=r0+δ;ε0,ε1,ε2分别称为简谐系数和第一、第二非简谐系数.文献[11]给出FeSi原子相互作用势为
式中:Zm1,Zm2,Ze1,Ze2,α1,α2分别是关于Fe和Si的参数.
-
合金的吉布斯函数为原子相互作用能U0与晶格振动贡献Gph之和:
文献[10]给出Gph为
式中的R=N0kB为气体普适常数,
$ \mathit{D}\left( {\frac{{{\mathit{\theta }_\mathit{D}}}}{\mathit{T}}} \right)$ 是德拜函数,表示为简谐近似下,
考虑到原子非简谐振动后,
利用G与自由能F的关系式
得到合金的自由能F当简谐近似时,为
考虑到原子非简谐振动后,合金的自由能为
-
利用公式
$ \mathit{B}\left( \mathit{T} \right) = \mathit{v}{\left( {\frac{{{\partial ^2}\mathit{F}}}{{\partial {\mathit{v}^{\rm{2}}}}}} \right)_\mathit{T}}$ ,由(10)式得简谐近似的弹性模量等于T=0 K时的弹性模量B0.非简谐效应下则为将摩尔定容热容量
$ {\mathit{C}_\mathit{v}}{\rm{ = 3}}\mathit{RD}\left( {\frac{{{\mathit{\theta }_\mathit{D}}}}{\mathit{T}}} \right)$ 和(6)式代入(11)式,得到利用定压热容量Cp与G的关系式
由(7),(8)式得到简谐近似为
考虑到非简谐效应后,定压热容量为
由(13)和(14)式,得到非简谐项对定压热容量的贡献ΔCp(T)=Cp(T)-Cp0(T)为
-
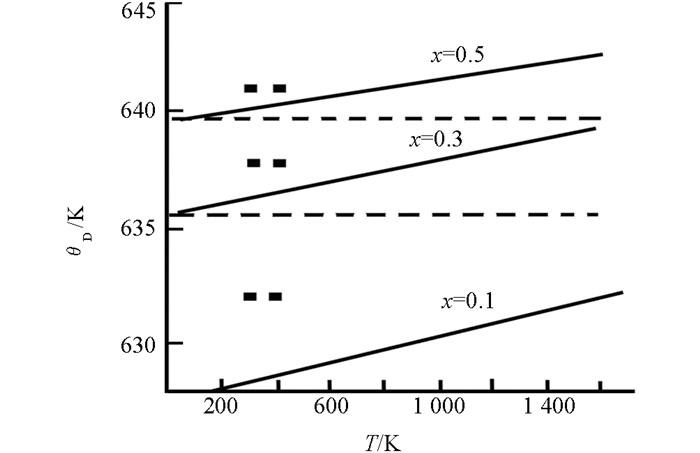
文献[10]给出了Fe,Co,Si的摩尔质量,容易求出杂质浓度分别为x=0.1,0.3,0.5时的平均摩尔质量,再由原子间距可得不同杂质浓度下的摩尔体积.文献[5]给出对Fe,Zm1=1.589 3,Ze1=0.226 0,α1=0.634 215;对Si,Zm2=1.331 4,Ze2=0.178 13,α2=0.521 485.由dφ/dr=0求得平衡位置两原子间距离r0=0.257 6 nm,进而求得简谐系数ε0、第一、二非简谐系数为ε1和ε2,再由ωD02=ε0/M,ħωD0=kBθD0,求得ωD0以及T=0 K时的德拜温度θD0,利用(5)式以及上述的结果,可得不同杂质浓度x下,不同温度时合金的德拜温度,由此可作出合金的德拜温度随温度的变化曲线(图 1),图 1中的实线是同时考虑到第一、二非简谐项的结果,虚线是简谐近似的结果,由此看出:①合金的德拜温度随温度的升高而降低,但变化非常缓慢.温度由0 K升高到1 600 K时,德拜温度只降低了3.3~4.5 K;②德拜温度随温度的升高而降低的程度,随着杂质浓度x的增大而增大;③本文给出在温度300 K时德拜温度的值与文献[10]的结果接近.
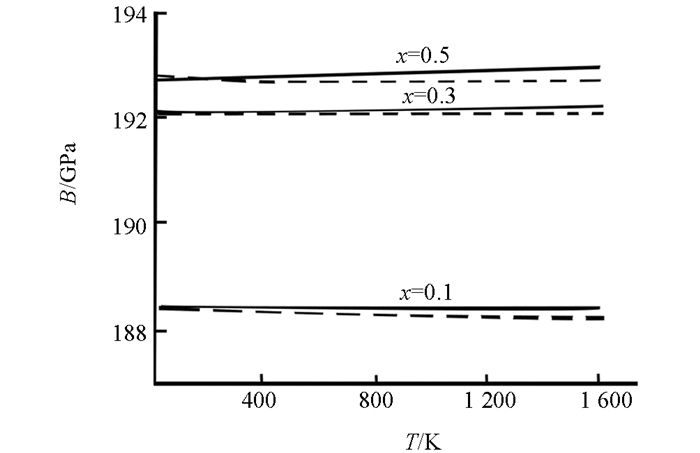
将得出的θD等值代入(3)式求得T=0 K时的弹性模量B0,将B0和不同温度下的θD值代入(12)式,可求得不同温度T时合金的弹性模量,由此作出弹性模量随温度的变化曲线见(图 2),图 2中的实线是同时考虑到第一、二非简谐项的结果,虚线是简谐近似的结果.由图 2看出:①合金的弹性模量随温度的升高而减小,但变化非常缓慢,温度由300 K升高到1 600 K时,只降低了1.3×10-3~2.2×10-3 GPa;②弹性模量随温度的升高而降低的程度,随着杂质浓度x的增大而增大;③本文给出在温度300 K时弹性模量的值与文献[10]的结果接近.
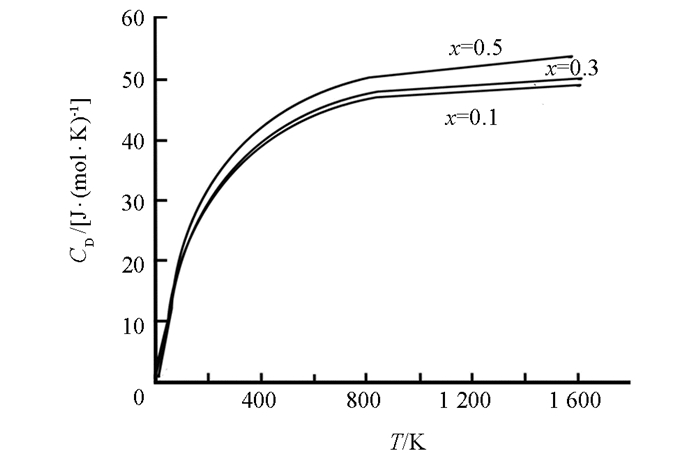
取1摩尔体积作计算,将R=8.31 J/(mol·k)代入(13)式得到简谐近似下不同温度时合金的定压热容量,并由此作出曲线(图 3),可看出:①温度较低时(低于380 K),定压热容量随温度升高而很快增大,而当温度高于800 K时,定压热容量随温度升高而缓慢变化,逐渐趋于常量;②在相同温度情况下,定压热容量随着杂质浓度的增大而增大,且温度愈高,杂质浓度的影响愈显著.
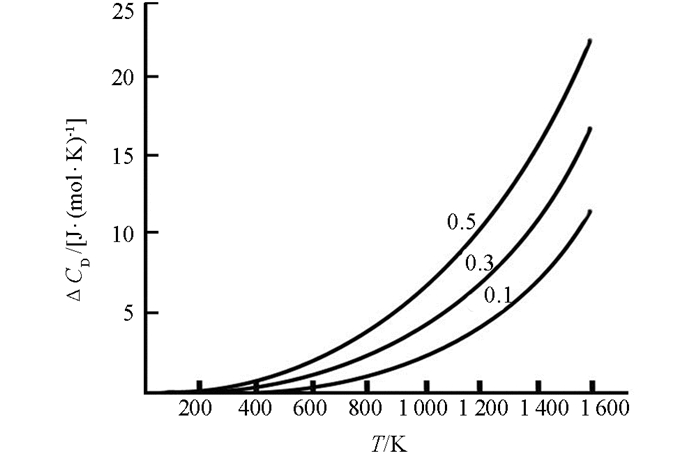
为反映非简谐效应的影响,将上述结果代入(15)式,得到非简谐项对合金定压热容的贡献量ΔCp随温度T的关系曲线(图 4),可看出:①温度较低时(低于700 K),非简谐项贡献量ΔCp随温度升高而缓慢增大,而当温度高于700 K时,则随温度升高而迅速增大;②在相同温度情况下,ΔCp随着杂质浓度的增大而增大,且温度愈高,杂质浓度和非简谐效应的影响愈显著.
-
1) Fe1-xCoxSi合金的德拜温度、弹性模量、热容量均随温度变化,其变化规律与掺钴杂质的浓度等有关,由(5)、(12)、(14)式表示;
2) Fe1-xCoxSi的德拜温度和弹性模量均随温度升高而减小,但变化非常缓慢,每升高1 K,德拜温度仅降低0.3%,弹性模量仅降低0.001%;而定压热容量随温度升高而非线性地增大,其中,温度较低时,近似遵从T3次方定律;温度较高时,热容量不趋于常量,而是随温度升高而缓慢增大;
3) 德拜温度和弹性模量随温度升高的降低程度以及非简谐项对热容量的影响大小均随含钴杂质浓度的增加而加大;
4) 若不考虑原子的非简谐效应,则Fe1-xCoxSi掺钴合金的德拜温度、弹性模量为常量,考虑到原子非简谐振动项后,则随温度变化而变化,温度愈高,杂质浓度和非简谐效应的影响愈显著.



 下载:
下载: