-
闭环供应链是将正向供应链和逆向供应链整合在一起的供应链系统,因其回收时间、数量、质量及加工过程的不确定性,增加了闭环供应链系统的复杂性,对供应链绩效产生了重要的影响;而且随着时代的发展,供应链成员中制造商和零售商均可以身兼数职,他们既可以直接参与销售环节作为销售商,又可以同时参与回收环节作为回收商,为供应链的回收渠道结构选择具有重要意义;再者随着环保知识的普及,消费者环保意识逐渐提高,会更加注重环境保护,抵制污染行为的发生[1],因而对废旧品各回收渠道的回收也会产生重要影响.因此,研究市场随机需求和消费者具有环保意识情形下的双回收渠道闭环供应链系统的定价对加强供应链节点企业间的协作、改善供应链的效益具有重大意义.
在考虑市场随机需求和消费者环保意识方面,大量的文献分别研究了随机需求和消费者具有环保意识下的闭环供应链定价决策问题.杨畅、程硕等在市场需求不确定的情况下,考虑市场需求依赖销售价格,建立了由单个供应商和单个零售商组成的二级退货模型[2].张克永等在不确定性需求下建立了由一个制造商和一个零售商构成的闭环供应链定价模型,研究了由制造商生产、销售、回收的集中决策以及由制造商生产、零售商回收的分散决策的最优策略[3].张翠基于随机需求,讨论供应链中的新产品和再制造品的价格存在差异时集中决策和分散决策下分别由制造商、零售商和第三方回收商单独参与回收的单渠道供应链定价模型,并定量分析了参数变化对不同回收模式最优策略的影响[4].张潜等构建了随机需求下基于制造商、零售商和第三方物流商组成的闭环供应链定价模型,并分别对模型在集中决策情形和分散决策情形的最优策略进行了分析[5].曹晓刚等研究了两个零售商存在竞争且面临不同随机市场需求的闭环供应链系统,并在集中决策和分散决策两种情形下分析了制造商和两个零售商的定价决策问题[6].易余胤等研究了需求不确定情形下由一个制造商和两个零售商组成的闭环供应链模型,得到了各成员的最优决策,并通过数值模拟的方法探讨了各参变量之间的相互关系[7]. Conrad研究了消费者环保意识如何影响购买环保产品的问题,结果表明消费者环保意识水平越高,越愿意支付更高的价格购买环保产品[8]. Chitra建立了双寡头垄断模型,研究了消费者环保意识对价格、产品特性以及竞争公司市场占有率的影响[9].熊中楷等在闭环供应链中考虑消费者环保意识因素,讨论了制造商的最优回收模型以及消费者环保意识对最优解的影响[10].钟劼从消费者体验的视角建立了购买行为影响因素模型,彻底分析了消费者在购买决策过程中功能因素和情感因素的影响[11].以上文献分别针对市场需求不确定的情形和消费者意识的单一回收渠道的闭环供应链进行了研究.
针对双渠道供应链的研究,唐秋生等基于准时制生产模式建立了需求不确定条件下“双源”、“双渠道”多周期闭环供应链库存优化模型[12].李健等在市场需求不确定条件下,研究了第三方回收商和零售商同时负责回收的闭环供应链系统,并在集中决策和分散决策两种情形下定量分析得到了各成员在不同回收率下的最优定价、最优订货量和最优利润[13].张晓丽建立了由单一零售商和众多消费者组成的二级供应链,研究了零售商线上预定和线下直销两种销售渠道[14]. Ferguson等研究了制造商在再制造领域面临竞争时其最优的生产策略[15].陈晓红等考虑消费者对产品功能质量和环境质量支付差异的情形,研究了制造商通过零售商直接销售新产品以及通过第三方销售旧产品的双销售渠道供应链系统定价问题,分析了政府补贴和消费者偏好对供应链的影响[16].李建斌等考虑双销售渠道的供应链系统定价问题,在网络零售商和实体零售商之间存在价格竞争和双向搭便车的情形下,研究了集成和分散两种模式下最优定价和努力水平决策[17].冯立樊等以WEEE回收商和处理商构成的两极逆向供应链为研究对象,讨论了消费者行为(回收渠道偏好和回收溢价)条件下,处理商回收渠道结构选择和双回收渠道协调问题[18-19].
上述文献分别研究了随机需求和消费者具有环保意识情形下的闭环供应链定价决策问题,以及随机需求和消费者行为条件下的双渠道问题.在现实生活中消费者具有环保意识且市场需求也是随机的,制造商和零售商都会参与电子废弃产品回收,而这几者并存的供应链的决策问题却没有文献进行研究.本文考虑随机市场需求和消费者具有环保意识并存的情形,研究制造商和零售商同时参与回收的闭环供应链的最优决策问题.
全文HTML
-
本文讨论的供应链中存在两种回收方式:一种是由制造商直接从消费者手中对具有一定利用价值或可以加工再利用的电子废弃物进行回收的直接回收方式;另一种是制造商通过零售商从消费者手中进行回收的间接回收方式.制造商的直接回收价格为pm,零售商的间接回收价格为pr,制造商从零售商处回收的转移价格为p0,制造商根据市场需求从零售商处回收的数量为Q0;由制造商以再造成本c将回收的废弃电子产品进行加工再造,形成有利用价值的再造产品,并以批发价格ω销售给零售商,零售商以价格p销售给消费者. πm,πr,π分别表示制造商、零售商和供应链系统的利润.制造商在供应链中起主导作用,作为Stackelberg博弈的领导者,而零售商则作为跟随者,在观察到制造商的决策之后做出自己的最优决策(图 1).
-
1) 制造商、零售商各自的回收量不仅受到自身回收价格的影响而且都受到对方回收价格的影响,并随自身价格增加而增加,随对方价格增加而减少.因此,制造商、零售商各自的回收量Qm,Qr分别表示为
其中a0表示消费者环保意识,即回收价格为零时的回收量;bm,br分别表示制造商和零售商的价格敏感度;β表示交叉价格敏感度.
2) 市场需求量为D(p,t)=td(p)=t(a-bp)(a>0,b>0),a表示市场规模,b表示市场需求的零售价格敏感度;t是在(0,m)上服从均匀分布的随机变量.
3) 制造商从零售商处回收的转移回收量不超过零售商的回收量,即Q0≤Qr,且没有进行再制造的电子废弃产品以其估计的残值s计入回收方的收益.
4) 模型中的参变量满足:① pr<p0,即回收商的回收价格小于制造商从零售商处回收的转移价格,保证零售商能从回收中获利;② pm<ω-c,即制造商回收单位价格小于制造商再造品的单位利润,保证制造商能从回收再造中获利;③ ω<p,即零售商从制造商处批发再造品的批发价格小于其零售价格,保证零售商销售有利可图;④ β<min{bm,br};⑤ bm<br,即零售商的价格敏感度大于制造商的价格敏感度,因为我们考虑到由于零售商直接面向消费者,所以零售商的回收价格变化对他回收数量的影响较大.
5) 不考虑新产品和再造产品之间的成本和质量等差异.
1.1. 问题描述
1.2. 基本假设
-
制造商利润包括收入、残值和成本,其中成本包括再制造品的制造成本、回收成本和从零售商处回收的转移成本.其利润为
零售商利润包括收入、残值和成本,其中成本包括从制造商处批发再造品的批发价格和回收成本.其利润为
因此,制造商和零售商的期望利润分别为
-
在集中决策情形下,制造商和零售商共同构成一个供应链系统,以求整个系统取得最大利润,共同决定各自最优回收量、最优回收价格.系统利润为
系统的期望利润为
对(5)式分别求关于pm,pr,Q0的偏导数,得
令
解得
将其代入方程组
得
由方程组(6)中第二式,解得
将其代入方程组(6)中第一式,得
将(7)式代入(1)、(2)式可得,制造商最优回收量
零售商最优回收量
制造商最优转移数量
将(7)、(8)、(9)、(10)式代入(5)式,可得集中决策下整个供应链的利润为
命题1 集中决策情形,制造商和零售商各自的回收价格均随消费者环保意识的增强而降低.
证 由β<min{bm,br}知,
且
即证.
命题2 集中决策情形,制造商和零售商的最优回收数量均随消费者环保意识的增强而增加.
证 由于
$\frac{{\partial Q_m^{1*}}}{{\partial {a_0}}} = \frac{{\partial Q_r^{1*}}}{{\partial {a_0}}} = \frac{1}{2} > 0$ ,即证.命题1和命题2说明在集中决策情形,随着消费者环保意识的增加,消费者将愿意以较低的回收价格甚至无偿将自己手中的电子废弃产品卖给制造商或零售商.
命题3 集中决策情形,整个供应链的利润随消费者环保意识的增强而增加.
证 由β<min{bm,br},则
即证.
命题3说明集中决策情形,随着消费者环保意识的增强,制造商、零售商将会以降低的回收价格回收更多的废弃电子产品,从而制造商可生产更多再制造电子产品,节约了制造成本,从而提高了整个供应链的利润.
-
由于制造商为博弈的领导者,则第一阶段由制造商确定电子废弃物的最优回收价格和回收数量,使自己的期望利润最大;第二阶段由零售商根据制造商确定的价格和数量来决定自己的回收价格和回收数量,以期最大化自己的期望利润.于是该决策问题模型如下
对(3)式分别求关于pm,Q0的一阶条件,利用(4)式求关于pr的一阶条件,得
令
可得
将其代入E[πm]并求关于p0的偏导数,得
将
代入方程组
有
将(12)式联立方程
$\frac{{\partial E\left[{{\pi _m}} \right]}}{{\partial {p_0}}} = 0$ ,得到方程组由方程组(13)中第二式可得
根据Stackelberg博弈的逆推归纳法,先分析第二个阶段零售商的决策.在第二个阶段,零售商在给定pm,p0的情况下求使πr实现最大值的pr,这样的pr必须满足(14)式,而制造商知道自己在选择pm时零售商的最优回收价格pr2*.所以直接将(14)式代入方程组(13)中第一式和第三式可得制造商、零售商的最优决策变量
其中,Δ1=ω-c-s,Δ2=m(a-bp),Δ3=(ω-c)m(a-bp).
将(15)、(16)、(17)式代入(1)、(2)式可得制造商、零售商的最优回收量分别为
把(15)、(16)、(17)、(18)、(19)代入(3)、(4)式,可得制造商、零售商的最优期望利润为
因此整个供应链利润为π2*=πm2*+πr2*.
命题4 分散决策下制造商和零售商回收价格同样均随消费者环保意识的增强而减小.
证 由β<min{bm,br},Δ1>0,Δ2>0,p-ω>0,可知
即证.
2.1. 集中决策情形
2.2. 分散决策情形
-
为了更加直观清晰地显示出消费者环保意识对最优策略的影响,假定β=0.4,a=20,b=1,m=2,bm=0.5,br=0.6,p=17.5,ω=16.5,c=14,s=2,在集中决策和分散决策情形下分析消费者环保意识变化对供应链中各方最优策略的影响.
-
通过计算可以得到消费者环保意识a0变化时,各方的最优策略及最优利润(表 1).
从表 1可以看出,集中决策情形下,随着消费者环保意识的增强,制造商和零售商的回收价格不断减小,回收数量不断增加,制造商从零售商处转移回收量减少,整个供应链的利润不断增加.
-
通过计算得到消费者环保意识变化时分散决策情形各方的最优策略及最优利润(表 2).
由表 2可以得到结论:随着消费者环保意识增加,制造商和零售商回收价格和转移价格都降低,回收数量都会增加;但是由于制造商直接回收数量增加,从零售商处转移回收数量急剧减少,从而使得零售商利润大幅减少,制造商利润小幅增加,供应链系统总利润减少.因而,分散决策情形下消费者环保意识的增加只有利于制造商.
-
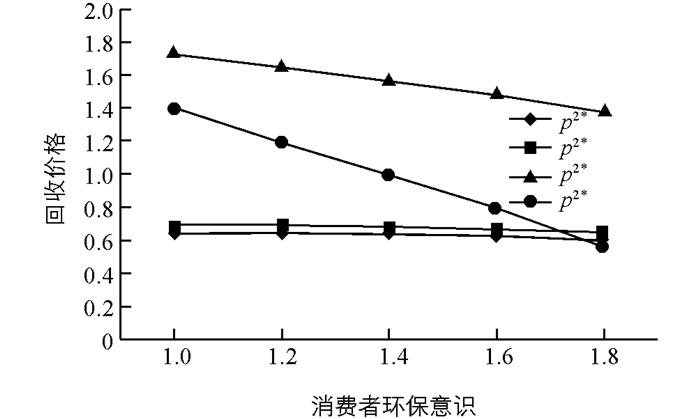
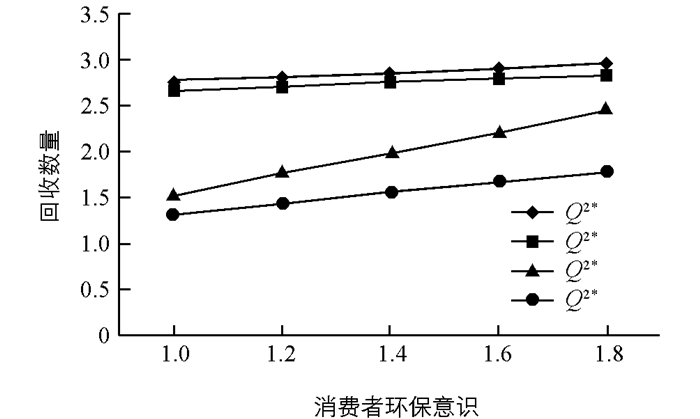
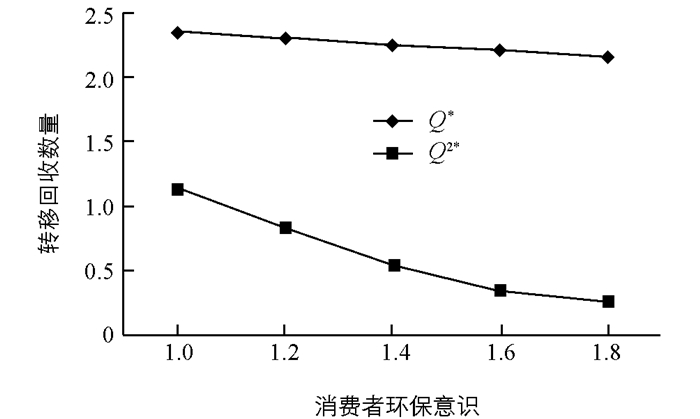
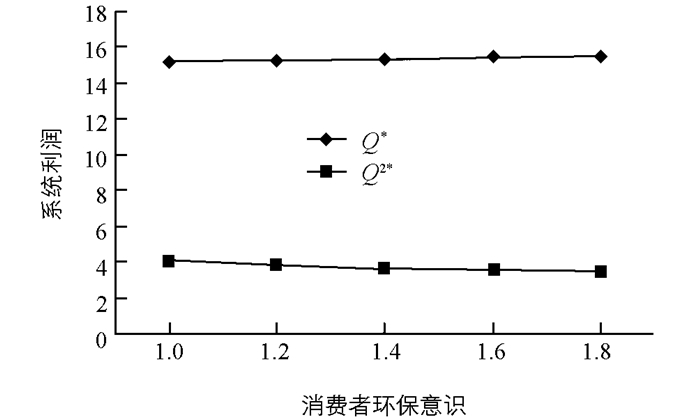
根据3.2中算例,我们得出不同决策模式下最优定价、回收量、转移回收量和系统利润的对比结果(图 2、图 3、图 4和图 5).
由图 2可知,随着消费者环保意识的增强,两种决策情形下制造商和零售商最优回收价格均下降,分散决策情形回收价格下降幅度大于集中决策情形,零售商的回收价格下降幅度大于制造商回收价格下降幅度.由图 3可知,集中决策情形回收数量大于分散决策的回收数量;随着消费者环保意识的增强,两种决策情形下制造商和零售商的回收数量都有增加,分散决策情形制造商回收数量增加的幅度大于零售商.由图 4和图 5可知,集中决策情形转移回收数量和供应链系统利润都大于分散决策情形;随着消费者环保意识的增强,两种决策情形制造商从零售商处转移回收数量减少,分散决策下转移回收的数量降速较大,导致零售商利润迅速减少,从而使得供应链系统在分散决策情形下利润减少.
3.1. 集中决策模型的参数分析
3.2. 分散决策模型的参数分析
3.3. 两种决策模式的参数比较
-
本文在随机需求和消费者具有环保意识的情形下考虑了制造商和零售商共同参与回收的双回收渠道闭环供应链定价问题,利用Stackelberg博弈得到了集中决策和分散决策两种情形下制造商和零售商的最优定价策略,并定性和定量分析了消费者环保意识变化对制造商和零售商各自最优决策变量和最优回收数量的影响.我们得到结论:在考虑市场随机需求和消费者环保意识的双渠道回收闭环供应链中,集中决策模型中最优回收价格低、供应链系统利润高且回收量相对较多;随着消费者环保意识的增加,制造商从零售商处转移回收数量急剧减少,直接回收数量增加,成本降低,从而使得制造商利润略有增加,零售商利润减少.因而,分散决策情形下消费者环保意识的增加只有利于制造商.




 下载:
下载: